Diagonal lines create dynamic visual interest by drawing the eye across the image, enhancing depth and movement in design and art. Incorporating diagonal elements can break the monotony of horizontal and vertical layouts, making your compositions more engaging and energetic. Explore the rest of this article to discover how to effectively use diagonal lines in your work for maximum impact.
Table of Comparison
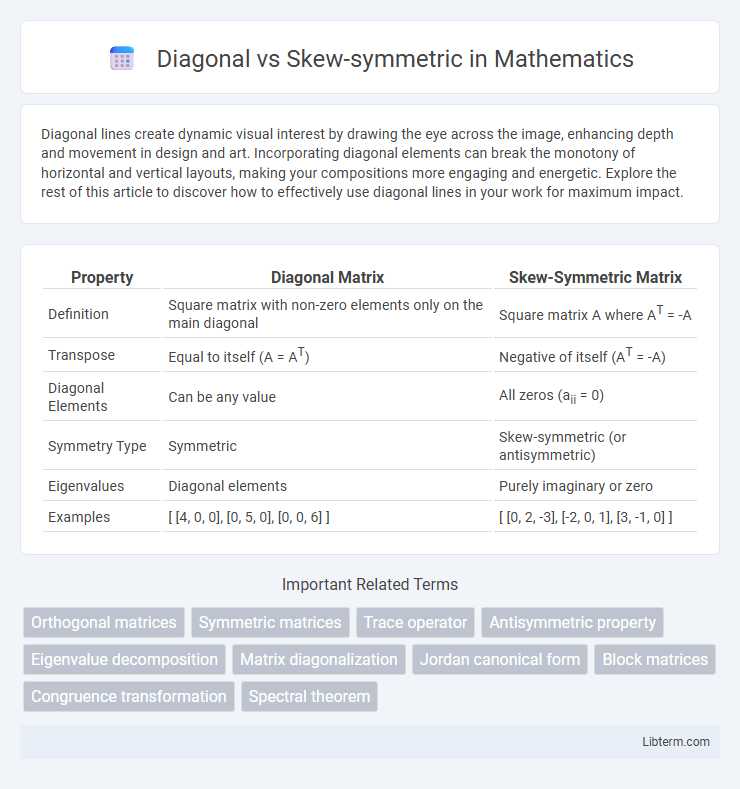
| Property | Diagonal Matrix | Skew-Symmetric Matrix |
|---|---|---|
| Definition | Square matrix with non-zero elements only on the main diagonal | Square matrix A where AT = -A |
| Transpose | Equal to itself (A = AT) | Negative of itself (AT = -A) |
| Diagonal Elements | Can be any value | All zeros (aii = 0) |
| Symmetry Type | Symmetric | Skew-symmetric (or antisymmetric) |
| Eigenvalues | Diagonal elements | Purely imaginary or zero |
| Examples | [ [4, 0, 0], [0, 5, 0], [0, 0, 6] ] | [ [0, 2, -3], [-2, 0, 1], [3, -1, 0] ] |
Introduction to Diagonal and Skew-Symmetric Matrices
Diagonal matrices are square matrices where all off-diagonal elements are zero, emphasizing simplicity in eigenvalue calculations and matrix operations. Skew-symmetric matrices are square matrices where the transpose equals the negative of the original matrix, characterized by zero diagonal entries and significant roles in antisymmetric transformations. Both matrix types are fundamental in linear algebra, with diagonal matrices providing straightforward eigen-structural insights and skew-symmetric matrices being crucial in physics and differential geometry.
Defining Diagonal Matrices
Diagonal matrices are square matrices where all off-diagonal elements are zero, meaning only the entries along the main diagonal can be nonzero, allowing for straightforward eigenvalue extraction and simplified matrix operations. Skew-symmetric matrices satisfy the condition A^T = -A, implying their diagonal elements must be zero, distinguishing them fundamentally from diagonal matrices. Understanding the strict structure of diagonal matrices aids in differentiating their properties and applications from those of skew-symmetric matrices.
Properties of Diagonal Matrices
Diagonal matrices feature nonzero elements solely along the main diagonal, ensuring their eigenvalues are precisely these diagonal entries and simplifying matrix operations like multiplication and exponentiation. Their symmetric nature means diagonal matrices are always equal to their transposes, which differs fundamentally from skew-symmetric matrices where the transpose equals the negative of the matrix. Diagonal matrices maintain commutativity under multiplication, a property not shared by general skew-symmetric matrices, highlighting their computational and theoretical advantages in linear algebra.
Defining Skew-Symmetric Matrices
Skew-symmetric matrices are square matrices \( A \) where the transpose equals the negative of the matrix, \( A^T = -A \), implying all diagonal elements are zero. In contrast to diagonal matrices, which have nonzero entries only on the main diagonal, skew-symmetric matrices have zeros on the diagonal and potentially nonzero elements off-diagonal arranged such that \( a_{ij} = -a_{ji} \). This defining property leads to important applications in physics and engineering, particularly in representing rotations and antisymmetric linear transformations.
Properties of Skew-Symmetric Matrices
Skew-symmetric matrices have the defining property that their transpose equals their negative, meaning \( A^T = -A \), which implies all diagonal elements are zero. The eigenvalues of skew-symmetric matrices are either zero or purely imaginary, reflecting their role in rotations and preservations of lengths in Euclidean spaces. They generate Lie algebras associated with orthogonal groups, crucial in differential geometry and physics for modeling antisymmetric transformations.
Key Differences Between Diagonal and Skew-Symmetric Matrices
Diagonal matrices contain nonzero elements only on their main diagonal, while skew-symmetric matrices have zero diagonal entries and satisfy the condition \(A^T = -A\). Diagonal matrices are always symmetric if their entries are real, whereas skew-symmetric matrices are inherently antisymmetric with off-diagonal elements that are negatives of each other. The eigenvalues of diagonal matrices are the diagonal entries themselves, but for skew-symmetric matrices, eigenvalues occur in purely imaginary conjugate pairs or zero when defined over real numbers.
Mathematical Examples: Diagonal vs Skew-Symmetric
Diagonal matrices have nonzero elements only on the main diagonal, such as \( \begin{bmatrix} 4 & 0 & 0 \\ 0 & -3 & 0 \\ 0 & 0 & 7 \end{bmatrix} \), while skew-symmetric matrices satisfy \( A^T = -A \) with zeroes on the diagonal, exemplified by \( \begin{bmatrix} 0 & 5 & -2 \\ -5 & 0 & 4 \\ 2 & -4 & 0 \end{bmatrix} \). The diagonal matrix elements represent eigenvalues directly, whereas skew-symmetric matrices have purely imaginary eigenvalues or zero. These fundamental differences illustrate distinct structural and spectral properties crucial in linear algebra and applications like physics and engineering.
Applications of Diagonal Matrices
Diagonal matrices streamline computations in linear algebra by simplifying eigenvalue problems, as their diagonal entries represent eigenvalues directly, making them essential in quantum mechanics and vibration analysis. They facilitate efficient storage and manipulation in numerical methods, especially in solving systems of linear equations and optimizing algorithms for large-scale data processing. Skew-symmetric matrices, in contrast, model rotational phenomena and are pivotal in physics and engineering, particularly in the study of angular velocity and rigid body dynamics.
Applications of Skew-Symmetric Matrices
Skew-symmetric matrices play a crucial role in physics and engineering by representing rotational transformations and angular velocities in three-dimensional space, particularly through their connection to the Lie algebra of the rotation group SO(3). In computer graphics and robotics, these matrices facilitate the modeling of rigid body motions and orientation changes using cross-product operators. Their inherent property of having zero diagonal entries aids in simplifying calculations involving antisymmetric bilinear forms and differential equations in dynamical systems.
Summary and Practical Implications
Diagonal matrices have nonzero elements only on their main diagonal, simplifying computations such as matrix multiplication and eigenvalue calculation, while skew-symmetric matrices have zeros on their diagonal and satisfy the condition A^T = -A, relevant in modeling rotations and antisymmetric relations. The diagonal structure facilitates efficient algorithms in linear algebra and systems solving, whereas skew-symmetric matrices are fundamental in physics and engineering for representing angular velocity and cross-product operations. Understanding the contrasting properties guides practical applications in numerical methods and the analysis of dynamical systems.
Diagonal Infographic
 libterm.com
libterm.com