A colimit in category theory generalizes constructions like unions, direct sums, and quotients by combining diagrams into a single universal object. Understanding colimits is essential for grasping how complex mathematical structures are built from simpler pieces within various categories. Dive into the rest of this article to explore colimits and their critical role in abstract mathematics.
Table of Comparison
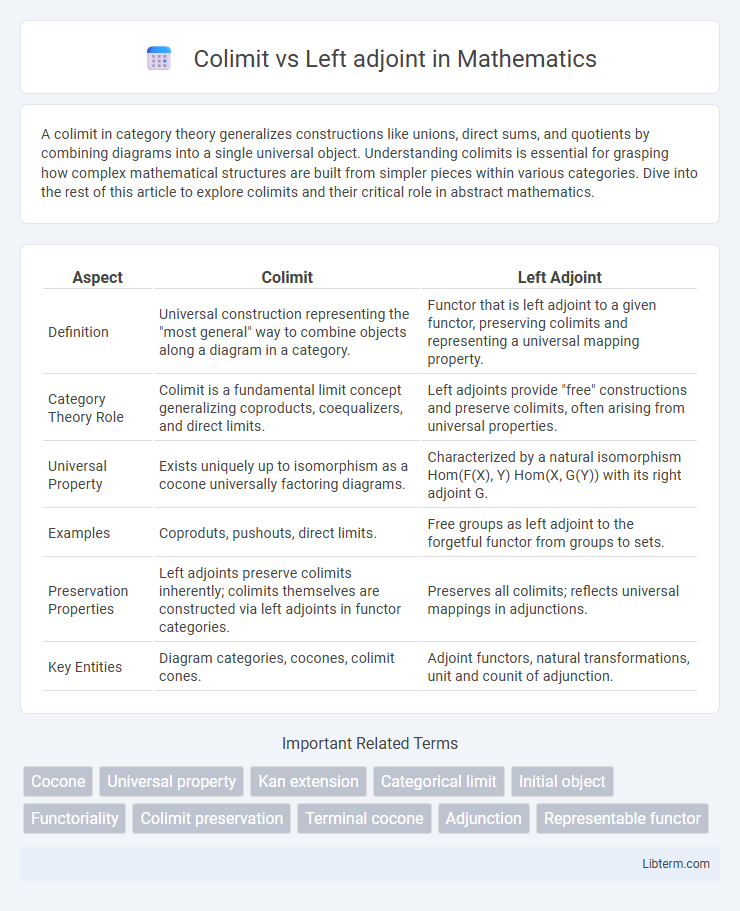
| Aspect | Colimit | Left Adjoint |
|---|---|---|
| Definition | Universal construction representing the "most general" way to combine objects along a diagram in a category. | Functor that is left adjoint to a given functor, preserving colimits and representing a universal mapping property. |
| Category Theory Role | Colimit is a fundamental limit concept generalizing coproducts, coequalizers, and direct limits. | Left adjoints provide "free" constructions and preserve colimits, often arising from universal properties. |
| Universal Property | Exists uniquely up to isomorphism as a cocone universally factoring diagrams. | Characterized by a natural isomorphism Hom(F(X), Y) Hom(X, G(Y)) with its right adjoint G. |
| Examples | Coproduts, pushouts, direct limits. | Free groups as left adjoint to the forgetful functor from groups to sets. |
| Preservation Properties | Left adjoints preserve colimits inherently; colimits themselves are constructed via left adjoints in functor categories. | Preserves all colimits; reflects universal mappings in adjunctions. |
| Key Entities | Diagram categories, cocones, colimit cones. | Adjoint functors, natural transformations, unit and counit of adjunction. |
Introduction to Colimits and Left Adjoints
Colimits represent a universal construction in category theory that generalizes operations like unions, direct limits, and coequalizers, serving as a fundamental tool for combining diagrams of objects. Left adjoints arise from adjoint functor pairs, preserving colimits and reflecting essential structural properties between categories. Understanding colimits through the lens of left adjoints reveals how these functors systematically construct colimits by transforming objects while maintaining categorical coherence.
Understanding Colimits in Category Theory
Colimits in category theory generalize constructions like unions, quotients, and direct limits, representing universal objects coalescing diagrams. A left adjoint functor preserves colimits by transforming colimit diagrams in the source category into colimits in the target category, reflecting a fundamental relationship between adjunctions and colimit preservation. Understanding this interplay clarifies how colimits serve as universal solutions and explains the structural role of left adjoints in functorial mappings across categories.
Defining Left Adjoints: Key Concepts
Left adjoints are functors that preserve colimits, characterized by a universal property establishing a natural isomorphism between hom-sets. They arise from an adjunction, where the left adjoint functor maps objects in a way that corresponds uniquely to morphisms in the target category. This fundamental concept is essential in category theory for understanding how structures transform while maintaining colimit consistency.
Relationship Between Colimits and Left Adjoints
Colimits in category theory often arise as the image of a diagram under a left adjoint functor, reflecting their fundamental relationship. Left adjoints preserve colimits, making them essential for constructing universal objects in various categories. This connection enables the translation of colimit computations into the language of adjunctions, streamlining categorical analysis and proofs.
Examples of Colimits in Mathematics
Colimits in mathematics generalize constructions like coproducts, pushouts, and direct limits, often appearing in categories such as sets, groups, and vector spaces. For example, the coproduct in the category of groups corresponds to the free product, while the pushout can model the amalgamation of groups along a common subgroup. Left adjoints frequently preserve colimits, as seen in free functors from sets to algebraic structures that realize colimits as free constructions.
Examples of Left Adjoints in Practice
Left adjoints frequently appear as free constructions in category theory, such as the free group functor assigning to each set its free group, exemplifying how left adjoints construct universal objects from given data. Another common instance is the tensor product functor in module categories, which serves as a left adjoint to the Hom functor, illustrating the relationship between linear maps and bilinear forms. These examples underscore the critical role of left adjoints in generating colimits and facilitating the transfer of structure across categories.
Universal Properties: Colimit vs Left Adjoint
Colimits and left adjoints both embody universal properties that characterize their roles in category theory. A colimit of a diagram represents a universal cocone, providing a unique factorization through it for any other cocone, while a left adjoint functor is defined by a universal mapping property that relates hom-sets via natural isomorphisms. Understanding the universal properties underlying colimits and left adjoints reveals their fundamental connections in constructing and representing objects and morphisms naturally within categorical frameworks.
Differences Between Colimits and Left Adjoints
Colimits are universal constructions that aggregate diagrams in a category, producing an object that coherently summarizes the diagram, while left adjoints are functors that preserve all colimits and establish adjunctions with right adjoints. The key difference lies in their roles: colimits are specific categorical limits focused on the gluing of objects and morphisms, whereas left adjoints are functorial mappings that transform objects between categories, often inducing colimits through their preservation properties. Understanding the distinction involves recognizing that colimits describe constructions internal to a category, while left adjoints are external processes defining functor relationships and inducing structure preservation across categories.
Applications in Algebra and Topology
Colimits and left adjoints play crucial roles in algebra and topology, with colimits often used to construct objects like coproducts and pushouts that unify structures, while left adjoints provide universal constructions that preserve colimits and facilitate the transfer of properties between categories. In algebra, colimits enable the formation of quotient groups and direct limits, essential in homological algebra and module theory, whereas left adjoint functors correspond to free constructions such as free groups or tensor algebras. Topologically, colimits describe gluing spaces along subspaces, fundamental in the study of CW complexes and fiber bundles, while left adjoints help construct universal coverings and localization functors, ensuring the preservation of homotopy colimits and homological invariants.
Summary: Choosing Between Colimit and Left Adjoint
Colimits generalize constructions like unions and coequalizers, providing a universal way to amalgamate diagrams in a category, while left adjoints preserve colimits and reflect a functor's ability to construct free or canonical objects. Choosing between using a colimit or a left adjoint hinges on whether the problem involves assembling data from a diagram (favoring colimits) or finding an optimal, structure-preserving functor with a universal property (favoring left adjoints). The decision impacts categorical constructions, with colimits addressing aggregation needs and left adjoints ensuring existence of universal solutions in functorial contexts.
Colimit Infographic
 libterm.com
libterm.com