Discrete space refers to a mathematical or topological structure where points are isolated from each other, meaning each singleton set is an open set. This property makes discrete spaces fundamental in computer science, graph theory, and digital topology because they model systems with distinct, separate elements. Explore the rest of the article to understand how discrete spaces play a crucial role in various applications and theoretical frameworks.
Table of Comparison
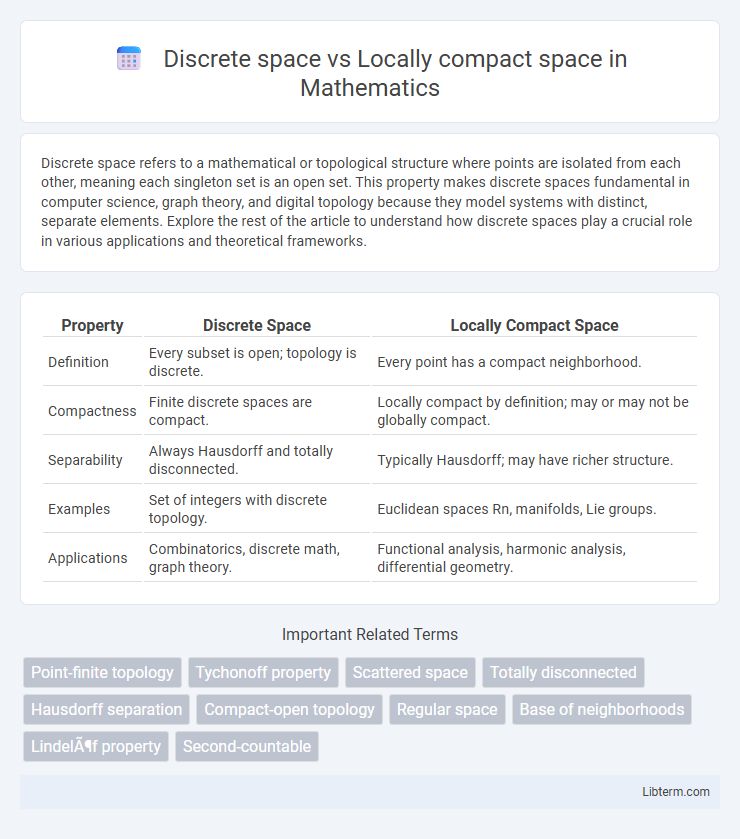
| Property | Discrete Space | Locally Compact Space |
|---|---|---|
| Definition | Every subset is open; topology is discrete. | Every point has a compact neighborhood. |
| Compactness | Finite discrete spaces are compact. | Locally compact by definition; may or may not be globally compact. |
| Separability | Always Hausdorff and totally disconnected. | Typically Hausdorff; may have richer structure. |
| Examples | Set of integers with discrete topology. | Euclidean spaces Rn, manifolds, Lie groups. |
| Applications | Combinatorics, discrete math, graph theory. | Functional analysis, harmonic analysis, differential geometry. |
Introduction to Topological Spaces
A discrete space is a topological space where every subset is open, providing the finest possible topology and simplifying concepts like continuity and convergence. Locally compact spaces, in contrast, allow every point to have a compact neighborhood, enabling powerful theorems in analysis and topology, such as the Riesz representation theorem and Tychonoff's theorem. Understanding these spaces within the framework of topological spaces highlights fundamental differences in their structure, affecting properties like compactness, connectedness, and separability.
Defining Discrete Spaces
A discrete space is a topological space where every singleton set is open, meaning each point forms an open set by itself. This property ensures the discrete topology induces maximal separation between points, contrasting with locally compact spaces, which require every point to have a compact neighborhood. Discrete spaces are trivially locally compact since singletons are compact, but not all locally compact spaces are discrete, as they may possess more complex neighborhood structures.
Understanding Locally Compact Spaces
Locally compact spaces are topological spaces where every point has a neighborhood whose closure is compact, offering a balance between local finiteness and global structure. Unlike discrete spaces, which treat all points as isolated with open singletons, locally compact spaces allow richer topology, enabling tools like Haar measure construction on locally compact groups. Understanding locally compactness is essential for advanced analysis and harmonic analysis since it generalizes compactness while retaining control over local behavior.
Key Differences: Discrete vs Locally Compact
A discrete space is characterized by every subset being open, resulting in isolated points and simple topological structure, while a locally compact space requires every point to have a compact neighborhood, enabling richer local properties. Discrete spaces are always locally compact because finite sets (including singletons) are compact, but the converse is not true as locally compact spaces can contain non-isolated points and more complex structures. Key differences lie in local compactness allowing for continuity and limit points, whereas discrete spaces lack these features due to their isolated nature.
Properties of Discrete Spaces
Discrete spaces possess the property that every subset is open, making them totally disconnected and zero-dimensional. These spaces are also trivially locally compact since every point has a compact neighborhood, specifically the singleton containing the point. The discrete topology ensures completeness and metrizability, with each point forming a clopen set, which sharply contrasts with the broader class of locally compact spaces that may not have such strong separation properties.
Properties of Locally Compact Spaces
Locally compact spaces possess the property that every point has a neighborhood whose closure is compact, enabling the extension of many results from compact spaces to more general settings. Unlike discrete spaces, which are locally compact because every singleton set is open and compact, locally compact spaces can be non-discrete and still retain vital compactness features important in analysis and topology. This property facilitates the use of tools like the Riesz representation theorem and supports the development of locally compact groups and measures.
Examples of Discrete Spaces
Discrete spaces consist of sets where every subset is open, such as finite sets like {1, 2, 3} or the integers with the discrete topology. These spaces are trivially locally compact because singletons are compact neighborhoods. In contrast, locally compact spaces include a broader class like the real line R with its usual topology, which is not discrete but possesses compact neighborhoods around each point.
Examples of Locally Compact Spaces
Locally compact spaces include Euclidean spaces \(\mathbb{R}^n\) with standard topology, where every point has a compact neighborhood such as closed balls. Another example is the discrete space on any set, since singletons are compact neighborhoods, highlighting that discrete spaces are a special case of locally compact spaces. Spaces like the unit circle \(S^1\) and more generally, manifolds, exhibit local compactness due to their locally Euclidean structure.
Applications in Mathematics and Physics
Discrete spaces, characterized by isolated points with no limit points, serve foundational roles in combinatorics, graph theory, and digital topology, modeling systems with finite or countable states. Locally compact spaces, defined by each point having a compact neighborhood, underpin functional analysis and harmonic analysis, facilitating the study of measures, distributions, and group representations essential in quantum mechanics and signal processing. The distinction between these spaces enables precise formulations of boundary conditions in differential equations and informs the structure of phase spaces in classical and quantum physics.
Conclusion: Choosing the Right Space
Discrete spaces offer simplicity and ease of analysis due to their isolated points and straightforward topology, making them ideal for combinatorial and computational applications. Locally compact spaces provide richer structures with useful properties like support for Haar measure and applicability in harmonic analysis, enhancing their role in advanced mathematical and physical theories. Selecting the right space depends on balancing simplicity with functional requirements, where discrete spaces excel in detail-oriented tasks while locally compact spaces suit contexts demanding continuity and compactness.
Discrete space Infographic
 libterm.com
libterm.com