The Artin-Schreier Theorem characterizes certain field extensions in characteristic p, describing how every cyclic extension of degree p can be expressed using Artin-Schreier polynomials. This result plays a crucial role in understanding the structure of fields and their automorphisms, especially in algebraic number theory and algebraic geometry. Discover more about the theorem's implications and applications in the rest of the article.
Table of Comparison
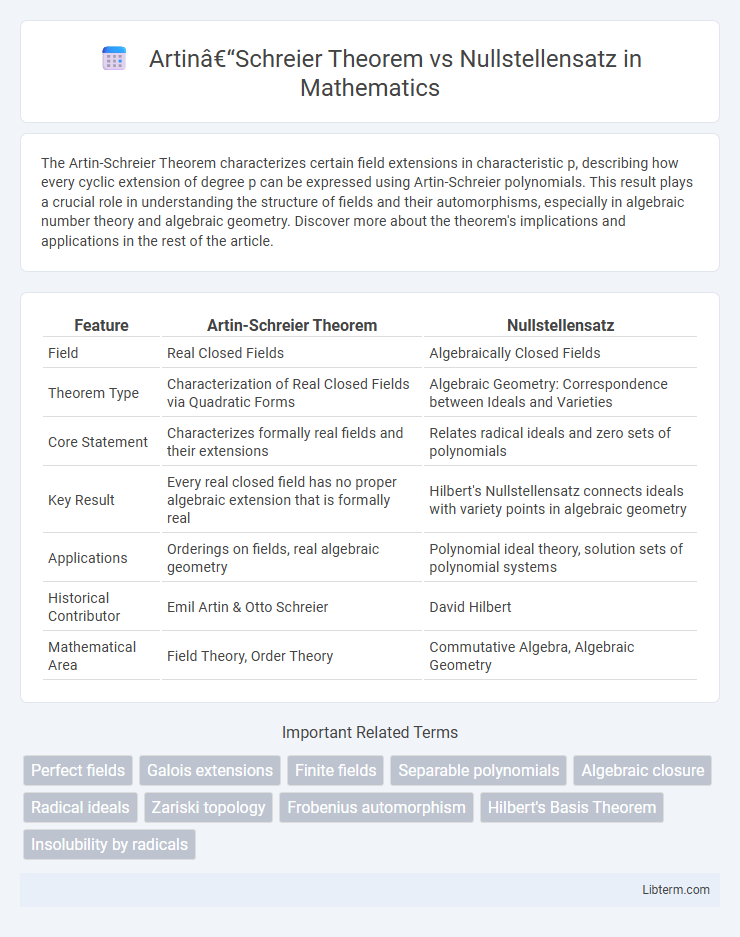
| Feature | Artin-Schreier Theorem | Nullstellensatz |
|---|---|---|
| Field | Real Closed Fields | Algebraically Closed Fields |
| Theorem Type | Characterization of Real Closed Fields via Quadratic Forms | Algebraic Geometry: Correspondence between Ideals and Varieties |
| Core Statement | Characterizes formally real fields and their extensions | Relates radical ideals and zero sets of polynomials |
| Key Result | Every real closed field has no proper algebraic extension that is formally real | Hilbert's Nullstellensatz connects ideals with variety points in algebraic geometry |
| Applications | Orderings on fields, real algebraic geometry | Polynomial ideal theory, solution sets of polynomial systems |
| Historical Contributor | Emil Artin & Otto Schreier | David Hilbert |
| Mathematical Area | Field Theory, Order Theory | Commutative Algebra, Algebraic Geometry |
Introduction to Artin–Schreier Theorem and Nullstellensatz
The Artin-Schreier Theorem characterizes real closed fields by stating that a formally real field has no proper algebraic extension that is formally real. In contrast, Hilbert's Nullstellensatz establishes a fundamental bridge between algebraic geometry and commutative algebra by linking ideals in polynomial rings over algebraically closed fields to their zero loci. Both theorems serve foundational roles: the Artin-Schreier Theorem in ordering field structures and the Nullstellensatz in describing solution sets of polynomial equations.
Historical Context and Mathematical Significance
The Artin-Schreier Theorem, developed in the early 20th century, revolutionized real algebra by characterizing formally real fields and their orderings, laying groundwork for real algebraic geometry. The Nullstellensatz, introduced by Hilbert in 1893, established a foundational link between algebraic geometry and commutative algebra by relating ideals in polynomial rings to algebraic sets over algebraically closed fields. Both results are pivotal: Artin-Schreier advanced the understanding of field orderings while Nullstellensatz provided the algebraic backbone for solving polynomial equations, shaping modern algebraic geometry.
Key Concepts and Definitions
The Artin-Schreier Theorem characterizes real closed fields through orderings, stating that such fields cannot be ordered algebraically extended without losing real closure, while the Nullstellensatz provides a foundational link between algebraic geometry and commutative algebra by relating ideals in polynomial rings over algebraically closed fields to their zero sets. Key concepts in the Artin-Schreier Theorem include ordered fields, real closure, and the notion of formally real fields, whereas the Nullstellensatz involves maximal ideals, variety points, and algebraic closure. Definitions crucial to understanding these theorems emphasize algebraic structures: for Artin-Schreier, ordered fields and real closedness; for the Nullstellensatz, polynomial ideals and affine algebraic varieties.
Field Extensions: Roles in Each Theorem
The Artin-Schreier Theorem characterizes real closed fields and their algebraic extensions, establishing that any finite field extension of a real closed field is either trivial or obtained by adjoining a square root of -1, emphasizing orderability and field embeddings. In contrast, the Nullstellensatz provides a foundational link between algebraic geometry and field theory by relating ideals in polynomial rings over algebraically closed fields to their zero sets, with field extensions playing a crucial role in determining solution fields for polynomial systems. Both theorems utilize field extensions to bridge algebraic structures and geometry, yet Artin-Schreier focuses on order and realness in fields while Nullstellensatz centers on algebraic closure and geometric solutions.
Algebraic Geometry vs Algebra: Domains of Application
The Artin-Schreier Theorem primarily applies to real algebraic geometry, characterizing real closed fields and providing tools for understanding orderings in algebraic structures. In contrast, the Nullstellensatz is a foundational result in complex algebraic geometry, linking ideals in polynomial rings to algebraic sets and establishing a correspondence that underpins the study of varieties over algebraically closed fields. While the Artin-Schreier framework addresses field orderings and real solutions, the Nullstellensatz enables the translation between geometric objects and algebraic ideals in higher-dimensional complex varieties.
Statement of the Artin–Schreier Theorem
The Artin-Schreier Theorem states that a formally real field can be ordered if and only if -1 is not expressible as a sum of squares in that field, providing a characterization of formally real fields. In contrast, the Nullstellensatz describes the correspondence between ideals in polynomial rings over algebraically closed fields and their common zeros, forming a cornerstone in algebraic geometry. The Artin-Schreier result is fundamental in real algebra and fields theory, while the Nullstellensatz connects algebraic structures with geometric loci in complex algebraic varieties.
Statement of Hilbert’s Nullstellensatz
Hilbert's Nullstellensatz asserts that for an algebraically closed field \( k \), if a polynomial \( f \in k[x_1, \ldots, x_n] \) vanishes on the common zero set of an ideal \( I \), then some power \( f^m \) belongs to \( I \). This theorem establishes a profound connection between algebraic varieties and ideals in polynomial rings, characterizing the radical of \( I \) as the set of all polynomials vanishing on its variety. In contrast, the Artin-Schreier theorem focuses on real closed fields and ordered structures, addressing extensions of fields rather than algebraic geometry foundations.
Comparative Analysis: Structure and Implications
The Artin-Schreier Theorem characterizes real closed fields by stating that a field is real closed if and only if it has no proper algebraic real extensions, highlighting the structural property of orderings and real algebraic closures. In contrast, Hilbert's Nullstellensatz establishes a fundamental correspondence between radical ideals in polynomial rings over algebraically closed fields and algebraic sets, underpinning affine algebraic geometry through ideal-variety duality. While the Artin-Schreier Theorem focuses on ordered field structures and their real extensions, the Nullstellensatz provides the algebraic backbone for solving polynomial equations and understanding geometric solution sets in algebraically closed fields, reflecting distinct but complementary algebraic frameworks.
Applications in Modern Mathematics
The Artin-Schreier Theorem plays a crucial role in real algebraic geometry by characterizing real closed fields, which are foundational in solving polynomial equations with ordered structures. In contrast, the Nullstellensatz is central to algebraic geometry, linking ideals in polynomial rings to geometric varieties over algebraically closed fields, enabling the study of solution sets of polynomial systems. Modern applications leverage the Artin-Schreier framework in decision theory and model theory, while the Nullstellensatz supports computational algebra, coding theory, and cryptography through its geometric insights into polynomial solution spaces.
Conclusion: Interrelations and Distinctions
The Artin-Schreier Theorem characterizes real-closed fields through the solvability of certain quadratic equations, establishing foundational properties of ordered fields and their algebraic extensions. In contrast, the Nullstellensatz links ideals in polynomial rings over algebraically closed fields to geometric solutions, forming a cornerstone of algebraic geometry. Together, these theorems illustrate distinct frameworks: the Artin-Schreier Theorem governs field orderings and real algebraic structures, while the Nullstellensatz bridges algebra and geometry via solution sets of polynomial equations.
Artin–Schreier Theorem Infographic
 libterm.com
libterm.com