Chain complexes are fundamental structures in algebraic topology, consisting of a sequence of abelian groups connected by boundary operators that satisfy the property of composing to zero. They provide a powerful framework to compute homology, helping to identify and classify topological spaces based on their holes and cycles. Explore the rest of the article to understand how chain complexes reveal deep insights into geometric and algebraic structures.
Table of Comparison
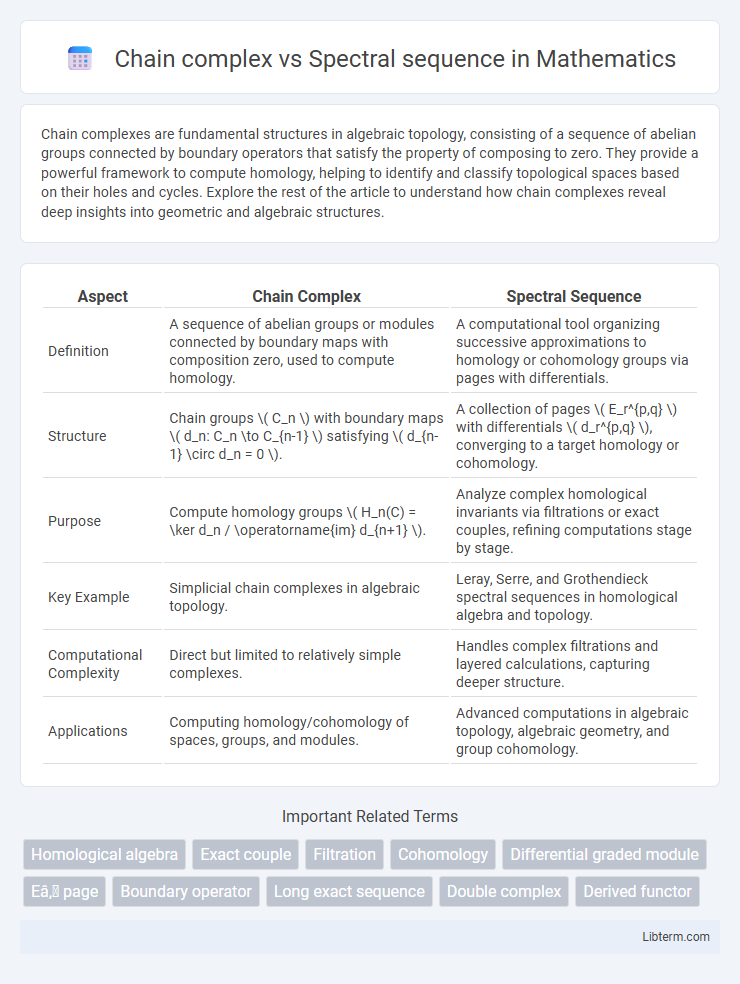
| Aspect | Chain Complex | Spectral Sequence |
|---|---|---|
| Definition | A sequence of abelian groups or modules connected by boundary maps with composition zero, used to compute homology. | A computational tool organizing successive approximations to homology or cohomology groups via pages with differentials. |
| Structure | Chain groups \( C_n \) with boundary maps \( d_n: C_n \to C_{n-1} \) satisfying \( d_{n-1} \circ d_n = 0 \). | A collection of pages \( E_r^{p,q} \) with differentials \( d_r^{p,q} \), converging to a target homology or cohomology. |
| Purpose | Compute homology groups \( H_n(C) = \ker d_n / \operatorname{im} d_{n+1} \). | Analyze complex homological invariants via filtrations or exact couples, refining computations stage by stage. |
| Key Example | Simplicial chain complexes in algebraic topology. | Leray, Serre, and Grothendieck spectral sequences in homological algebra and topology. |
| Computational Complexity | Direct but limited to relatively simple complexes. | Handles complex filtrations and layered calculations, capturing deeper structure. |
| Applications | Computing homology/cohomology of spaces, groups, and modules. | Advanced computations in algebraic topology, algebraic geometry, and group cohomology. |
Introduction to Chain Complexes and Spectral Sequences
Chain complexes consist of sequences of abelian groups or modules connected by boundary operators whose composition is zero, serving as fundamental structures in homological algebra to compute homology groups. Spectral sequences provide a computational tool that approximates the homology or cohomology of complex filtered chain complexes through successive pages, revealing intricate algebraic structures and convergences. These methods are essential in algebraic topology and algebraic geometry for systematically analyzing algebraic invariants and resolving complex homological problems.
Fundamental Definitions and Concepts
A chain complex is a sequence of abelian groups or modules connected by boundary operators whose composition is zero, encoding algebraic structures derived from topological spaces. Spectral sequences are computational tools that provide successive approximations to the homology or cohomology groups of a filtered chain complex, structured as a collection of pages with differentials refining each stage. The fundamental difference lies in chain complexes representing algebraic data directly, while spectral sequences analyze filtered chain complexes through iterative homological approximations.
Structure and Construction of Chain Complexes
Chain complexes consist of a sequence of abelian groups or modules connected by boundary operators where the composition of consecutive maps is zero, ensuring exactness at each stage. Their structure facilitates the computation of homology by breaking complex problems into manageable pieces through filtration and grading. Spectral sequences arise from filtered chain complexes, providing a layered approximation method that converges to the homology of the original complex, capturing subtle structural information beyond immediate homology groups.
Overview of Spectral Sequences
Spectral sequences provide a powerful tool for computing homology and cohomology by filtering complex algebraic structures into successive approximations, which converge to the desired invariants. Unlike chain complexes that organize algebraic objects linearly with boundary maps, spectral sequences decompose computations into multiple pages, revealing intricate layers of algebraic relationships. This layered approach allows for step-by-step analysis, making spectral sequences essential in advanced algebraic topology and homological algebra.
Key Differences Between Chain Complexes and Spectral Sequences
Chain complexes consist of sequences of abelian groups or modules connected by boundary operators, serving as fundamental tools in homological algebra for computing homology groups. Spectral sequences provide a computational framework to approximate complex homology or cohomology groups through successive pages and filtrations, revealing deeper structural information step-by-step. The key difference lies in that chain complexes form the initial algebraic data with boundary maps, while spectral sequences organize and refine this data across stages to unravel intricate algebraic invariants.
Applications in Algebraic Topology and Homological Algebra
Chain complexes provide a fundamental tool for computing homology groups, enabling the classification of topological spaces and the study of their algebraic invariants. Spectral sequences offer a powerful computational technique to handle filtered chain complexes, facilitating the step-by-step calculation of homology or cohomology groups in more complex algebraic or topological structures. These methods are central to advanced topics such as fiber bundle analysis, sheaf cohomology, and derived functor computations in algebraic topology and homological algebra.
Computation Techniques: Chain Complex vs Spectral Sequence
Chain complexes provide a linear algebra framework for computing homology by explicitly handling boundary operators and cycles, enabling direct calculation of homology groups. Spectral sequences offer a powerful computational technique for filtering complex structures into successive approximations, converging to the desired homology through page-by-page differential computations. The choice between chain complexes and spectral sequences depends on the complexity and layered structure of the problem, with spectral sequences being particularly effective for multi-filtered or hierarchical topological spaces.
Examples Demonstrating Each Framework
Chain complexes appear in algebraic topology through singular homology, where sequences of abelian groups linked by boundary maps capture topological spaces' structure; for example, the chain complex of a simplicial complex assigns groups to each simplex dimension, facilitating homology computation. Spectral sequences offer a powerful computational tool in filtered chain complexes or double complexes, such as the Leray spectral sequence in sheaf cohomology, which relates the cohomology of a space to that of a continuous map's fibers. Both frameworks enable stepwise homological algebra calculations, but spectral sequences handle more complex filtrations and convergences, exemplified by the Serre spectral sequence calculating the homology of a fibration from base and fiber data.
Advantages and Limitations
Chain complexes provide a straightforward algebraic framework for computing homology groups, making them well-suited for problems with direct boundary mappings and simple filtration structures. Spectral sequences offer a powerful, step-by-step computational tool that decomposes complex topological and algebraic structures into manageable layers, enabling the analysis of graded modules and filtered complexes. While chain complexes excel in clarity and ease of use for basic homological calculations, spectral sequences present limitations in complexity and steep learning curves but greatly expand the capacity to handle intricate filtrations and convergence issues.
Conclusion: Choosing the Right Tool for Mathematical Problems
Chain complexes provide a foundational framework for computing homology and understanding exact sequences, making them ideal for direct algebraic computations in topology and algebraic geometry. Spectral sequences offer a powerful iterative method to approximate complex homological invariants, especially when dealing with filtered complexes or multi-graded structures. Selecting between chain complexes and spectral sequences depends on the problem's complexity and the need for stepwise refinement versus straightforward homological calculation.
Chain complex Infographic
 libterm.com
libterm.com