A principal ideal is an ideal in a ring generated by a single element, meaning every element of the ideal can be expressed as that generator multiplied by an element of the ring. Understanding principal ideals is crucial for exploring the structure of rings, particularly in fields like algebraic number theory and commutative algebra. Dive into the rest of the article to learn how principal ideals shape the foundation of ideal theory and its applications.
Table of Comparison
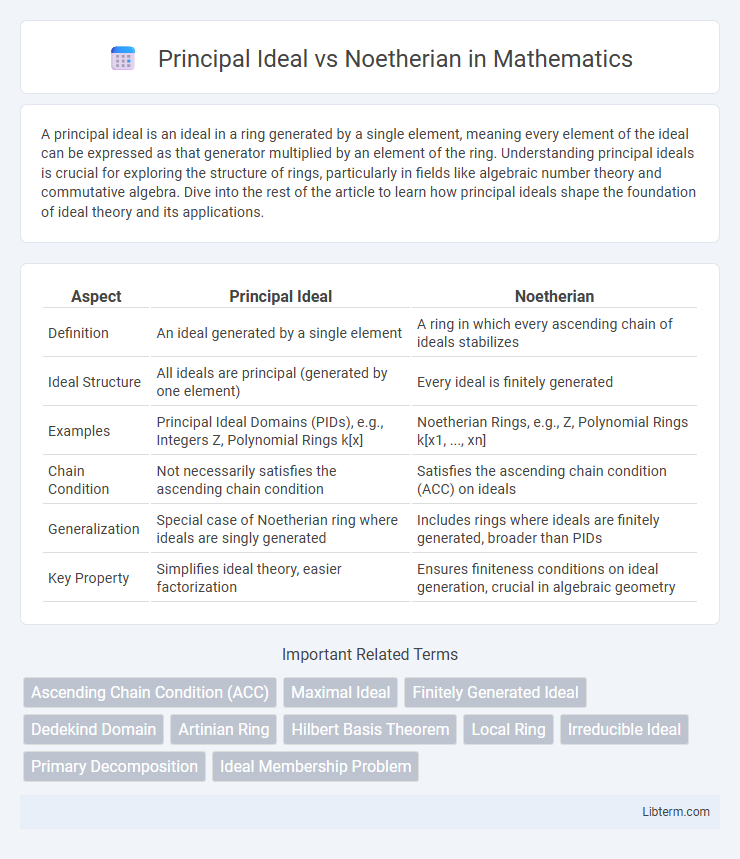
| Aspect | Principal Ideal | Noetherian |
|---|---|---|
| Definition | An ideal generated by a single element | A ring in which every ascending chain of ideals stabilizes |
| Ideal Structure | All ideals are principal (generated by one element) | Every ideal is finitely generated |
| Examples | Principal Ideal Domains (PIDs), e.g., Integers Z, Polynomial Rings k[x] | Noetherian Rings, e.g., Z, Polynomial Rings k[x1, ..., xn] |
| Chain Condition | Not necessarily satisfies the ascending chain condition | Satisfies the ascending chain condition (ACC) on ideals |
| Generalization | Special case of Noetherian ring where ideals are singly generated | Includes rings where ideals are finitely generated, broader than PIDs |
| Key Property | Simplifies ideal theory, easier factorization | Ensures finiteness conditions on ideal generation, crucial in algebraic geometry |
Definition of Principal Ideal
A principal ideal in ring theory is an ideal generated by a single element, meaning every element within the ideal can be expressed as the product of that generator and some ring element. Noetherian rings, by definition, satisfy the ascending chain condition for ideals, ensuring every ideal is finitely generated but not necessarily principal. The distinction highlights that every principal ideal ring is Noetherian, but not all Noetherian rings have all ideals as principal ideals.
Understanding Noetherian Rings
Noetherian rings are characterized by the ascending chain condition on ideals, meaning every increasing sequence of ideals stabilizes, which ensures that every ideal is finitely generated. In contrast, principal ideal rings require each ideal to be generated by a single element, forming a stricter subclass of Noetherian rings. Understanding the Noetherian property is essential for algebraic geometry and commutative algebra, as it guarantees manageable ideal structures and the applicability of powerful theorems like Hilbert's Basis Theorem.
Key Differences Between Principal Ideal and Noetherian
A principal ideal is an ideal in a ring generated by a single element, while a Noetherian ring satisfies the ascending chain condition on ideals, ensuring every ideal is finitely generated. Principal ideal domains (PIDs) are a special class of Noetherian rings where all ideals are generated by one element, but not all Noetherian rings are PIDs. The key difference lies in generation constraints: principal ideals require single generators, whereas Noetherian rings allow finitely many generators without restricting to a single element.
Examples of Principal Ideal Domains
Principal Ideal Domains (PIDs) are integral domains where every ideal is generated by a single element, exemplified by the ring of integers \(\mathbb{Z}\) and polynomial rings over a field like \(\mathbb{F}[x]\). In contrast, Noetherian rings guarantee every ascending chain of ideals stabilizes, but not necessarily that every ideal is principal, as seen in polynomial rings with multiple variables such as \(\mathbb{F}[x,y]\). The distinction highlights that while all PIDs are Noetherian, the converse does not hold, with PIDs serving as a stricter subclass characterized by simpler ideal structures.
Properties of Noetherian Rings
Noetherian rings are characterized by the ascending chain condition on ideals, ensuring every increasing sequence of ideals stabilizes, which guarantees that every ideal is finitely generated. In contrast, principal ideal rings require all ideals to be generated by a single element, a stricter condition not necessarily met by Noetherian rings. The finiteness properties of Noetherian rings enable effective management of ideal structures and facilitate key results in algebraic geometry and commutative algebra.
Principal Ideal Rings vs Noetherian Rings
Principal Ideal Rings (PIRs) are commutative rings in which every ideal is generated by a single element, emphasizing simplicity and structure in ideal formation. Noetherian Rings generalize this by requiring only that every ascending chain of ideals stabilizes, ensuring manageability without restricting ideal generation to one element. While all Principal Ideal Rings are Noetherian, the converse is not true, highlighting the broader conditions captured by Noetherian Rings compared to the more restrictive structure of PIRs.
Characterization Theorems
Principal ideal domains (PIDs) are characterized by the theorem stating every ideal is generated by a single element, ensuring a simple structure of ideals. Noetherian rings satisfy the ascending chain condition on ideals, meaning all increasing sequences of ideals stabilize, which guarantees finite generation of every ideal. The fundamental characterization theorem for Noetherian rings establishes that any ideal is finitely generated, linking the condition to key algebraic properties distinct from the single-generator property of PIDs.
Importance in Abstract Algebra
Principal ideal domains (PIDs) are a crucial class of rings in abstract algebra where every ideal is generated by a single element, simplifying the structure and making factorization unique. Noetherian rings, defined by the ascending chain condition on ideals, ensure all ideals are finitely generated, which generalizes the finiteness condition in PIDs and guarantees that many algebraic processes terminate. The importance of these concepts lies in their foundational role in ring theory, module theory, and algebraic geometry, providing tools for understanding factorization, ideal structure, and decomposition in algebraic systems.
Applications and Implications
Principal Ideal Domains (PIDs) simplify algebraic structures by ensuring every ideal is generated by a single element, facilitating computations in number theory and algebraic geometry. Noetherian rings, characterized by the ascending chain condition on ideals, guarantee finiteness properties crucial for algorithm termination in computational algebra and the study of ring homomorphisms. The distinction between PIDs and Noetherian rings impacts module classification, factorization properties, and the feasibility of solving polynomial equations in various mathematical and applied contexts.
Summary: Principal Ideal vs Noetherian
A Principal Ideal Domain (PID) is an integral domain in which every ideal is generated by a single element, simplifying the structure of the ring's ideals. A Noetherian ring, by contrast, requires that every ascending chain of ideals stabilizes, ensuring no infinite strictly increasing sequences of ideals but not necessarily principal generation. While all PIDs are Noetherian due to their finitely generated ideals, not all Noetherian rings are PIDs, making the principal ideal property a stronger and more specific condition within ring theory.
Principal Ideal Infographic
 libterm.com
libterm.com