A free group is a fundamental concept in abstract algebra where every element can be written uniquely as a product of generators and their inverses without any relations other than those required by group axioms. These groups serve as a building block for more complex structures and are crucial in understanding group theory's applications in topology, geometry, and combinatorics. Explore the rest of the article to deepen Your understanding of free groups and their significance in mathematics.
Table of Comparison
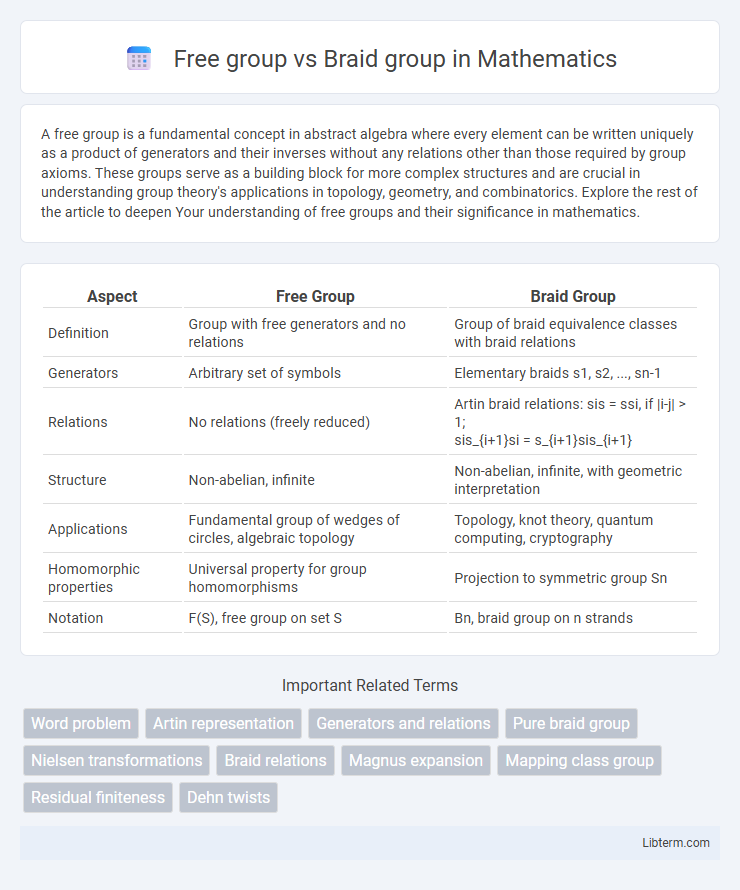
| Aspect | Free Group | Braid Group |
|---|---|---|
| Definition | Group with free generators and no relations | Group of braid equivalence classes with braid relations |
| Generators | Arbitrary set of symbols | Elementary braids s1, s2, ..., sn-1 |
| Relations | No relations (freely reduced) | Artin braid relations:
sis = ssi, if |i-j| > 1; sis_{i+1}si = s_{i+1}sis_{i+1} |
| Structure | Non-abelian, infinite | Non-abelian, infinite, with geometric interpretation |
| Applications | Fundamental group of wedges of circles, algebraic topology | Topology, knot theory, quantum computing, cryptography |
| Homomorphic properties | Universal property for group homomorphisms | Projection to symmetric group Sn |
| Notation | F(S), free group on set S | Bn, braid group on n strands |
Introduction to Free Groups and Braid Groups
Free groups consist of elements generated by a set where no relations exist other than the group axioms, making them fundamental objects in algebraic topology and combinatorial group theory. Braid groups, introduced by Emil Artin, are generated by braids on n strands with specific relations modeling the intertwining of strands, playing a critical role in knot theory and geometric group theory. Both structures serve as key examples of groups with distinct presentations: free groups have freely generating sets, while braid groups have generators subject to braid relations reflecting their topological origins.
Fundamental Definitions and Concepts
A free group is defined as a group with a basis set of generators having no relations other than those necessary to satisfy group axioms, allowing every element to be represented uniquely as a reduced word in these generators. In contrast, a braid group, denoted \( B_n \) for \( n \) strands, is generated by elementary braids subject to Artin relations, capturing the topological properties of intertwining strands. The fundamental group structure of braid groups links them to mapping class groups and configuration spaces, while free groups represent the simplest non-abelian groups characterized by their universal mapping property.
Generators and Relations in Free Groups
Free groups are generated by a set of elements with no relations other than those required by group axioms, meaning each element is a unique reduced word formed from the generators and their inverses. Braid groups, by contrast, have generators subject to specific relations known as braid relations, such as the Artin relations, which encode the twisting and crossing of strands. The absence of relations in free groups results in a simpler structure, whereas braid groups' additional relations create a more complex algebraic and geometric framework.
Structure and Properties of Braid Groups
Braid groups, denoted \( B_n \), are infinite non-abelian groups generated by \( n-1 \) Artin generators that satisfy specific braid relations, contrasting with free groups which have no relations between generators. The defining relations in braid groups encode the topological properties of braids, making these groups fundamental in knot theory and algebraic topology. Their structure exhibits a rich interplay of combinatorial and geometric properties, including a well-understood center, solvable word problem, and connections to mapping class groups.
Geometric Interpretations: Free vs Braid Groups
Free groups represent collections of loops based at a single point in a topological space, with no relations other than the identity, capturing pure combinatorial freedom in path concatenation. Braid groups, on the other hand, arise from configurations of intertwining strands in three-dimensional space, embodying geometric entanglements governed by Artin's relations reflecting over- and under-crossings. The fundamental contrast lies in how free groups model abstract loop concatenations without spatial constraints, while braid groups encode intricate spatial interactions and knotting phenomena through their geometric representations.
Algebraic Presentations and Differences
Free groups are algebraically presented by a set of generators with no relations other than the group axioms, effectively allowing every element to be written uniquely as a reduced word in the generators and their inverses. Braid groups, denoted \( B_n \), extend this structure by having generators \(\sigma_1, \sigma_2, \ldots, \sigma_{n-1}\) with defining relations describing the braid relations: \(\sigma_i \sigma_j = \sigma_j \sigma_i\) for \(|i - j| > 1\) and \(\sigma_i \sigma_{i+1} \sigma_i = \sigma_{i+1} \sigma_i \sigma_{i+1}\), encoding the over-and-under crossings of strands. The fundamental difference is that free groups impose no relations beyond inverse pairs, yielding a free algebraic structure, whereas braid groups possess intricate relations reflecting topological constraints, making them richer and more complex objects in geometric group theory.
Applications in Topology and Algebra
Free groups serve as foundational structures in algebraic topology for modeling fundamental groups of wedge sums of circles, enabling classification of topological spaces via their loop spaces. Braid groups, characterized by generators corresponding to strand crossings, play a crucial role in knot theory and the study of configuration spaces, providing algebraic invariants that classify braids and links. Applications in topology leverage braid groups to understand mapping class groups and monodromy actions, while in algebra they facilitate solutions to the word and conjugacy problems as well as representations critical for quantum groups and statistical mechanics.
Homomorphisms between Free and Braid Groups
Homomorphisms between free groups and braid groups reveal complex algebraic structures, where each generator of a free group maps to braid group elements that satisfy braid relations. These mappings often preserve group operations but reflect topological properties inherent in braid groups, such as the intertwining of strands. Studying these homomorphisms aids in understanding the transformation of abstract free group elements into concrete braid configurations and their applications in knot theory and algebraic topology.
Subgroup Structures and Complexity
Free groups possess a straightforward subgroup structure characterized by the Nielsen-Schreier theorem, which ensures every subgroup is itself free and often of infinite rank, reflecting relatively low algebraic complexity. In contrast, braid groups exhibit richer and more intricate subgroup configurations, including non-free subgroups and complex normal forms tied to Garside structures, resulting in higher algorithmic and combinatorial complexity. The decision problems related to subgroup membership and conjugacy in braid groups are generally more complex than in free groups due to their nonlinear relations and topological origins.
Key Differences and Open Problems
Free groups are algebraic structures generated by a set of elements with no relations other than the group axioms, leading to a basis of freely reduced words, while braid groups consist of generators subject to specific braid relations reflecting the topological properties of braids. Key differences include the complexity of relations; free groups have trivial relations, whereas braid groups feature nontrivial Artin relations that encode the entanglement of strands. Open problems in braid groups involve the classification of their representations and the word and conjugacy problems, whereas free groups primarily pose challenges in understanding their automorphism groups and subgroup structure.
Free group Infographic
 libterm.com
libterm.com