The permutation symbol, often represented by the Greek letter epsilon (e), is a mathematical notation used to express the sign of a permutation and to compute determinants. It plays a crucial role in tensor calculus and vector algebra by simplifying the expression of cross products and alternating sums. Explore the rest of the article to understand how the permutation symbol can enhance your grasp of advanced mathematical concepts.
Table of Comparison
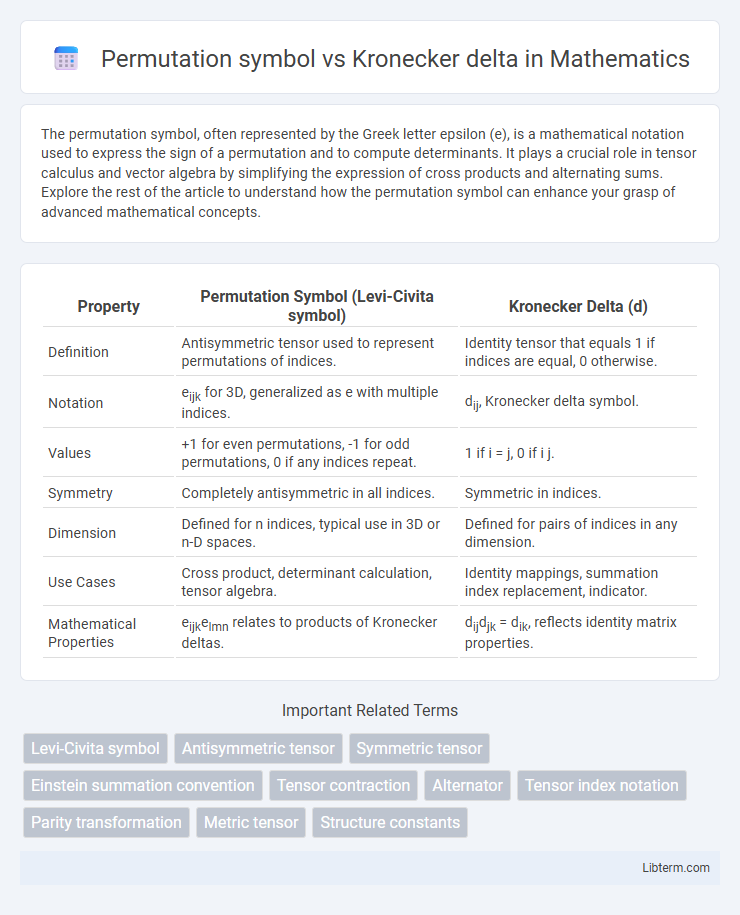
| Property | Permutation Symbol (Levi-Civita symbol) | Kronecker Delta (d) |
|---|---|---|
| Definition | Antisymmetric tensor used to represent permutations of indices. | Identity tensor that equals 1 if indices are equal, 0 otherwise. |
| Notation | eijk for 3D, generalized as e with multiple indices. | dij, Kronecker delta symbol. |
| Values | +1 for even permutations, -1 for odd permutations, 0 if any indices repeat. | 1 if i = j, 0 if i j. |
| Symmetry | Completely antisymmetric in all indices. | Symmetric in indices. |
| Dimension | Defined for n indices, typical use in 3D or n-D spaces. | Defined for pairs of indices in any dimension. |
| Use Cases | Cross product, determinant calculation, tensor algebra. | Identity mappings, summation index replacement, indicator. |
| Mathematical Properties | eijkelmn relates to products of Kronecker deltas. | dijdjk = dik, reflects identity matrix properties. |
Introduction to Permutation Symbol and Kronecker Delta
The permutation symbol, also known as the Levi-Civita symbol, is a tensor used to express antisymmetric properties in permutations of indices, frequently applied in vector calculus and tensor analysis. The Kronecker delta, represented as di, functions as an identity element in index notation, equating to 1 when indices are equal and 0 otherwise, simplifying summations and transformations. Both symbols serve as fundamental tools in mathematical physics and engineering for manipulating multi-index equations and expressing properties of tensors concisely.
Definitions: Permutation Symbol vs Kronecker Delta
The permutation symbol, often denoted as e_ijk, is an antisymmetric tensor used to represent the sign of a permutation of indices, taking values +1, -1, or 0 depending on whether the permutation is even, odd, or contains repeated indices. The Kronecker delta, d_ij, functions as an identity tensor equal to 1 when its indices are equal and 0 otherwise, serving as a discrete analog of the Dirac delta function in finite-dimensional spaces. Both symbols are fundamental in tensor calculus and linear algebra, with the permutation symbol capturing orientation and antisymmetry, while the Kronecker delta expresses index equivalence and serves as a metric tensor in Euclidean spaces.
Notation and Representation
The permutation symbol, also known as the Levi-Civita symbol, is denoted by e_ijk and represents the sign of a permutation of indices, taking values of +1, -1, or 0 depending on the parity of the permutation and whether any indices are repeated. The Kronecker delta, d_ij, acts as the identity matrix element, equal to 1 if i = j and 0 otherwise, serving as a discrete analog of the Dirac delta function in finite dimensions. In tensor notation, e_ijk is used to express antisymmetric properties and cross products, while d_ij functions as the metric for index substitution and simplification in summation conventions.
Mathematical Properties
The permutation symbol, or Levi-Civita symbol e_{ijk}, is an antisymmetric tensor used to express cross products and determinants, with values of +1, -1, or 0 depending on the parity of the index permutation. The Kronecker delta d_{ij} acts as an identity matrix element in tensor operations, equal to 1 if i = j and 0 otherwise, serving as a metric tensor in Euclidean spaces. Their mathematical properties intersect in vector calculus identities, such as e_{ijk}e_{lmn} = det(d_{il} d_{im} d_{in}; d_{jl} d_{jm} d_{jn}; d_{kl} d_{km} d_{kn}), highlighting the relationship between antisymmetric tensors and identity mappings.
Key Differences Between Permutation Symbol and Kronecker Delta
The permutation symbol (Levi-Civita symbol) is an antisymmetric tensor used to express cross products and determinants, taking values of 0, 1, or -1 depending on the order of indices, while the Kronecker delta is a symmetric identity operator that equals 1 when indices are equal and 0 otherwise. The permutation symbol encodes orientation and sign changes under index permutations, making it essential in vector calculus and tensor operations, whereas the Kronecker delta functions as an indexing tool for selecting components and simplifying summations. Key differences include the tensor rank, symmetry properties, and their roles in vector operations versus identity mappings in algebraic expressions.
Applications in Linear Algebra
The permutation symbol (Levi-Civita symbol) is essential in linear algebra for expressing cross products, determinants, and antisymmetric tensors, facilitating computations involving orientation and volume in vector spaces. The Kronecker delta serves as the identity element in tensor notation, simplifying summation expressions and transforming coordinates by acting as the identity matrix in index notation. Both symbols streamline tensor operations and play crucial roles in matrix theory, particularly in simplifying expressions of eigenvalues, eigenvectors, and matrix transformations.
Role in Tensor Calculus
The permutation symbol (Levi-Civita symbol) plays a crucial role in tensor calculus by encoding the antisymmetric properties of tensors, facilitating the expression of cross products and determinants in multiple dimensions. The Kronecker delta acts as the identity tensor, simplifying index manipulations by serving as a substitution tool in tensor contractions and transformations. Together, these symbols enable compact representation and computation of tensor operations fundamental to differential geometry and physics.
Example Calculations
The permutation symbol \(\epsilon_{ijk}\) calculates the signed volume or orientation of three vectors, with \(\epsilon_{123} = 1\) indicating an even permutation, while the Kronecker delta \(\delta_{ij}\) serves as the identity matrix element, \(\delta_{12} = 0\) and \(\delta_{11} = 1\). Example calculations show \(\epsilon_{ijk}\epsilon_{lmk} = \delta_{il}\delta_{jm} - \delta_{im}\delta_{jl}\), which simplifies cross product identities in vector algebra. Using these properties, the vector triple product \(\mathbf{a} \times (\mathbf{b} \times \mathbf{c})\) can be expressed through Kronecker deltas, illustrating the efficiency of these symbols in multilinear algebra.
Common Mistakes and Misconceptions
The permutation symbol, also known as the Levi-Civita symbol, often gets confused with the Kronecker delta due to their similar indexing notations but fundamentally represent different concepts; the permutation symbol encodes the sign of a permutation, while the Kronecker delta acts as an identity operator in index notation. A common mistake is treating the Levi-Civita symbol as symmetric when it is strictly antisymmetric, leading to incorrect sign assignments in tensor calculations. Misconceptions also arise when users interchange the roles of these symbols in expansions, such as using the Kronecker delta to swap indices in antisymmetric tensors, which can produce erroneous results in vector calculus and physics applications.
Conclusion and Summary
The permutation symbol \(\varepsilon_{ijk}\) captures the orientation and handedness of coordinate systems, offering a concise representation of antisymmetric properties in vector and tensor operations. In contrast, the Kronecker delta \(\delta_{ij}\) acts as the identity element in index notation, simplifying expressions involving orthogonality and selection rules by equating indices. Together, these symbols streamline tensor algebra by encoding symmetry and identity constraints fundamental to physics and engineering computations.
Permutation symbol Infographic
 libterm.com
libterm.com