A quotient group is formed by partitioning a group into disjoint cosets of a normal subgroup, capturing the group's structure at a higher level of abstraction. This construction simplifies complex group properties while preserving operation consistency, playing a crucial role in group theory and algebraic studies. Discover how quotient groups fundamentally shape modern mathematics by exploring the detailed concepts ahead.
Table of Comparison
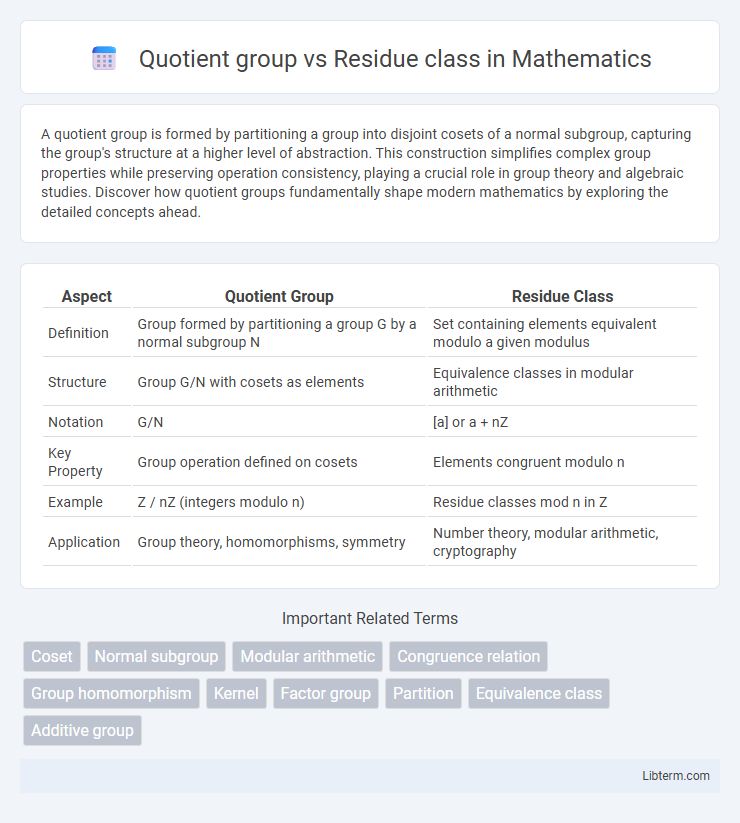
| Aspect | Quotient Group | Residue Class |
|---|---|---|
| Definition | Group formed by partitioning a group G by a normal subgroup N | Set containing elements equivalent modulo a given modulus |
| Structure | Group G/N with cosets as elements | Equivalence classes in modular arithmetic |
| Notation | G/N | [a] or a + nZ |
| Key Property | Group operation defined on cosets | Elements congruent modulo n |
| Example | Z / nZ (integers modulo n) | Residue classes mod n in Z |
| Application | Group theory, homomorphisms, symmetry | Number theory, modular arithmetic, cryptography |
Introduction to Quotient Groups and Residue Classes
Quotient groups arise from partitioning a group by a normal subgroup, forming cosets that create a new group structure reflecting the original group's symmetry. Residue classes, often encountered in modular arithmetic, represent equivalence classes of integers under congruence relations, which are specific instances of quotient sets. Understanding quotient groups generalizes the concept of residue classes by applying equivalence relations within abstract algebraic structures.
Fundamental Definitions
A quotient group is formed by partitioning a group G into cosets of a normal subgroup N, where each element of the quotient group corresponds to a distinct coset gN, ensuring group structure on the set of these cosets. A residue class, primarily used in modular arithmetic, represents the set of all integers congruent to a given integer modulo n, effectively partitioning the integers into equivalence classes based on the modulus n. Both concepts involve equivalence relations and partitioning sets into classes, but quotient groups generalize the idea to abstract groups with normal subgroups, while residue classes are specific to integers modulo n.
Construction of Quotient Groups
The construction of quotient groups involves partitioning a group \( G \) by a normal subgroup \( N \), forming cosets that serve as elements of the quotient group \( G/N \). Each coset represents a residue class modulo \( N \), capturing equivalence under the subgroup's relation. This quotient structure preserves group operations through well-defined multiplication of cosets, facilitating analysis of group homomorphisms and factor groups.
Structure of Residue Classes
Residue classes form a partition of a group into disjoint subsets, each representing cosets of a normal subgroup, which collectively define a quotient group structure. The structure of residue classes reflects the algebraic properties of the quotient group, where each residue class corresponds to a distinct element in the quotient and operations between these classes mimic the original group's operation modulo the normal subgroup. Understanding the residue classes' formation and behavior is essential for analyzing the quotient group's properties, such as homomorphisms, factorization, and symmetry breaking within group theory.
Key Differences Between Quotient Groups and Residue Classes
Quotient groups are algebraic structures formed by dividing a group \( G \) by a normal subgroup \( N \), resulting in cosets that combine under group operation. Residue classes specifically refer to equivalence classes in modular arithmetic, where integers are grouped by their remainders after division by a modulus \( n \). The key difference lies in their contexts: quotient groups generalize group partitioning based on normal subgroups, while residue classes are a particular example of quotient groups applied to the additive group of integers modulo \( n \).
Similarities in Algebraic Properties
Quotient groups and residue classes both form partitions of a parent group into disjoint subsets, preserving group structure through equivalence relations defined by normal subgroups and modular arithmetic respectively. Each element in these constructions represents an entire coset or residue class, ensuring closure, associativity, identity, and invertibility hold within the quotient structure. Both share the fundamental property that operations performed on representatives correspond directly to operations on the resulting equivalence classes, maintaining the homomorphic image of the original group.
Examples Illustrating Quotient Groups
The quotient group Z/nZ, formed by the integers modulo n, illustrates a key example where the residue classes serve as the group elements under addition. For instance, Z/4Z consists of the residue classes {0, 1, 2, 3}, where addition is performed modulo 4, demonstrating how quotient groups partition a group into cosets. Another example is the quotient group formed by the symmetric group S_3 over its normal subgroup A_3, yielding a group isomorphic to Z/2Z, showing residue classes as distinct cosets representing group structure simplification.
Applications of Residue Classes in Number Theory
Residue classes serve as fundamental tools in number theory for simplifying complex calculations by categorizing integers based on modular equivalence, facilitating the solution of congruences and divisibility problems. Their applications extend to the development of cryptographic algorithms, such as RSA, where residue classes modulo a composite number underpin the security of encryption and decryption processes. Quotient groups generalize residue classes in abstract algebra, enabling deeper structural insights in algebraic number theory and group theory.
Role in Abstract Algebra and Modular Arithmetic
Quotient groups serve as fundamental structures in abstract algebra, enabling the partitioning of groups into cosets by normal subgroups to form new groups that reveal intrinsic algebraic properties. Residue classes play a pivotal role in modular arithmetic by grouping integers into equivalence classes modulo a fixed integer, facilitating computations in modular systems. Both concepts illustrate the use of equivalence relations to simplify complex algebraic objects and are essential in studying cyclic groups, ring theory, and number theory.
Summary and Comparative Insights
A quotient group is formed by partitioning a group \(G\) by a normal subgroup \(N\), where each coset represents an element of the quotient group \(G/N\), preserving group operation structure. Residue classes arise from modulo arithmetic, specifically partitioning integers into equivalence classes based on congruence modulo \(n\), effectively creating a finite ring or group known as \(\mathbb{Z}/n\mathbb{Z}\). While all residue classes form quotient groups under addition modulo \(n\), quotient groups generalize this concept to any group and normal subgroup, extending beyond integer arithmetic.
Quotient group Infographic
 libterm.com
libterm.com