Analytic space is a fundamental concept in complex analysis, referring to a complex manifold equipped with a sheaf of holomorphic functions that locally resemble open subsets of complex Euclidean space. This framework allows for the rigorous study of complex structures and their properties, facilitating advancements in several mathematical and physical theories. Explore the rest of this article to deepen your understanding of analytic spaces and their pivotal role in modern mathematics.
Table of Comparison
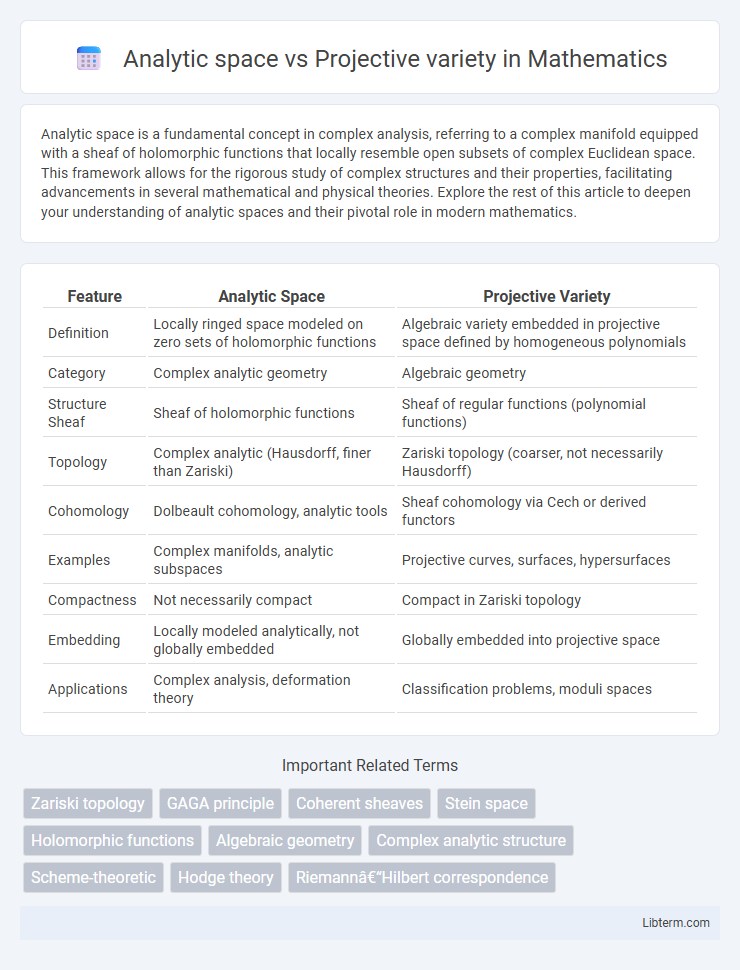
| Feature | Analytic Space | Projective Variety |
|---|---|---|
| Definition | Locally ringed space modeled on zero sets of holomorphic functions | Algebraic variety embedded in projective space defined by homogeneous polynomials |
| Category | Complex analytic geometry | Algebraic geometry |
| Structure Sheaf | Sheaf of holomorphic functions | Sheaf of regular functions (polynomial functions) |
| Topology | Complex analytic (Hausdorff, finer than Zariski) | Zariski topology (coarser, not necessarily Hausdorff) |
| Cohomology | Dolbeault cohomology, analytic tools | Sheaf cohomology via Cech or derived functors |
| Examples | Complex manifolds, analytic subspaces | Projective curves, surfaces, hypersurfaces |
| Compactness | Not necessarily compact | Compact in Zariski topology |
| Embedding | Locally modeled analytically, not globally embedded | Globally embedded into projective space |
| Applications | Complex analysis, deformation theory | Classification problems, moduli spaces |
Introduction to Analytic Spaces and Projective Varieties
Analytic spaces generalize complex manifolds by allowing singularities and locally modeling spaces as zero sets of analytic functions, facilitating the study of complex structures through sheaf theory and local ringed spaces. Projective varieties arise as zero loci of homogeneous polynomials in projective space, characterized by their algebraic properties and embedding in complex projective space, linking geometry with algebraic structures. Both frameworks serve as foundational objects in complex geometry, with analytic spaces emphasizing local analytic properties and projective varieties emphasizing global algebraic structures.
Historical Context and Development
The development of analytic spaces and projective varieties began with the emergence of complex analytic geometry and algebraic geometry in the early 20th century. Analytic spaces were formalized through the work of mathematicians such as Henri Cartan and Jean-Pierre Serre, focusing on locally ringed spaces defined by sheaves of holomorphic functions. Projective varieties originated from classical algebraic geometry, with foundational contributions by Guido Castelnuovo and Federigo Enriques, emphasizing varieties embedded in projective space defined by homogeneous polynomial equations.
Fundamental Definitions
Analytic spaces are locally modeled on zero sets of holomorphic functions in complex Euclidean spaces, equipped with a sheaf of holomorphic functions, emphasizing local analytic structure. Projective varieties are defined as the zero loci of homogeneous polynomials in projective space, carrying an algebraic structure governed by polynomial equations and graded coordinate rings. The key difference lies in analytic spaces being rooted in complex analysis for local properties, while projective varieties arise from algebraic geometry with a global polynomial framework.
Key Properties and Distinctions
Analytic spaces and projective varieties differ fundamentally in structure and topology; analytic spaces are locally modeled on convergent power series and can exhibit non-algebraic behavior, while projective varieties are defined algebraically as zero sets of homogeneous polynomials in projective space, inheriting a Zariski topology. Key properties of analytic spaces include being locally ringed spaces with sheaves of holomorphic functions, enabling complex analytic techniques and local uniformization, whereas projective varieties are rigid algebraic objects characterized by their homogeneity, compactness, and ample line bundles that facilitate embedding into projective space. Distinctions also arise in function theory and morphisms, as morphisms between analytic spaces need only preserve holomorphic structures, while morphisms of projective varieties respect algebraic structures and maintain algebraic dependencies, reflecting deep interactions between complex analysis and algebraic geometry.
Examples: Analytic Spaces versus Projective Varieties
Analytic spaces often arise in complex geometry as local models defined by convergent power series, such as the unit disk in \(\mathbb{C}\), whereas projective varieties are algebraic sets defined by homogeneous polynomials in projective space, like the projective curve given by \(x^2 + y^2 = z^2\) in \(\mathbb{P}^2\). An example highlighting their differences includes the complex analytic space defined by the zero set of \(f(z) = e^z - 1\) in \(\mathbb{C}\), which lacks an algebraic counterpart as a projective variety. Projective varieties exhibit algebraic rigidity with global polynomial equations, while analytic spaces allow more flexible local analytic structures, enabling the study of phenomena such as singularities and local deformations not captured in the purely algebraic setting.
Morphisms: Maps and Transformations
Morphisms between analytic spaces are defined by holomorphic maps preserving complex structure, whereas morphisms of projective varieties correspond to regular maps given by polynomial functions in projective coordinates. Analytic morphisms allow local power series expansions and are flexible in the complex analytic setting, while projective variety morphisms impose rigid algebraic constraints ensuring global polynomial behavior. Studying these morphisms highlights key differences in map continuity, local versus global definitions, and algebraic versus analytic frameworks in algebraic geometry.
Topological and Algebraic Structures
Analytic spaces are locally modeled on convergent power series rings, providing a richer topological structure with complex analytic topology that allows the study of finer geometric properties such as holomorphic functions and local analytic deformations. Projective varieties, defined by homogeneous polynomial equations in projective space, possess a Zariski topology that is coarser and emphasizes algebraic properties including dimension, singularities, and intersection theory. The interplay between these two frameworks enables the use of analytic techniques to investigate algebraic varieties, particularly through the GAGA principle, which establishes an equivalence between coherent sheaves in the analytic and algebraic categories for projective varieties.
Applications in Algebraic Geometry
Analytic spaces provide a flexible framework for studying local properties of complex algebraic varieties using tools from complex analytic geometry, such as sheaf cohomology and Hodge theory, enhancing understanding of singularities and deformation theory. Projective varieties, defined by homogeneous polynomial equations in projective space, serve as fundamental objects in algebraic geometry for global classification problems, intersection theory, and moduli space construction. The interplay between analytic spaces and projective varieties enables powerful techniques like GAGA theorems, linking algebraic and analytic categories and facilitating the transfer of results between complex analytic and algebraic settings.
Advantages and Limitations
Analytic spaces provide a flexible framework for studying local properties of complex varieties through holomorphic functions, enabling powerful tools like sheaf cohomology and resolution of singularities, which are essential for understanding complex analytic structures. Projective varieties benefit from algebraic methods, such as Hilbert's Nullstellensatz and well-defined notions of dimension and degree, making them suitable for global geometric and arithmetic investigations within algebraic geometry. However, analytic spaces often lack the algebraic structure required for certain global classification problems, while projective varieties can be rigid and less adaptable to local deformations and transcendental analysis.
Future Directions and Open Questions
Future research in the comparison between analytic spaces and projective varieties centers on understanding the deeper categorical equivalences and extending GAGA-type theorems to broader contexts such as non-Archimedean analytic geometry. Open questions include characterizing how the cohomological properties of coherent sheaves differ under various analytic and algebraic topologies and exploring moduli problems in complex and rigid analytic settings. Advancements in derived algebraic geometry and homotopical methods promise to unify the frameworks, offering new insights into deformation theory and mirror symmetry phenomena.
Analytic space Infographic
 libterm.com
libterm.com