Higher homotopy operations extend classical homotopy theory by providing sophisticated algebraic structures that capture intricate relationships between homotopy groups beyond primary operations. These operations play a crucial role in understanding spaces and spectra, enabling the classification of complex topological phenomena and advancing computational techniques in stable homotopy theory. Explore the rest of the article to deepen your understanding of higher homotopy operations and their applications in modern algebraic topology.
Table of Comparison
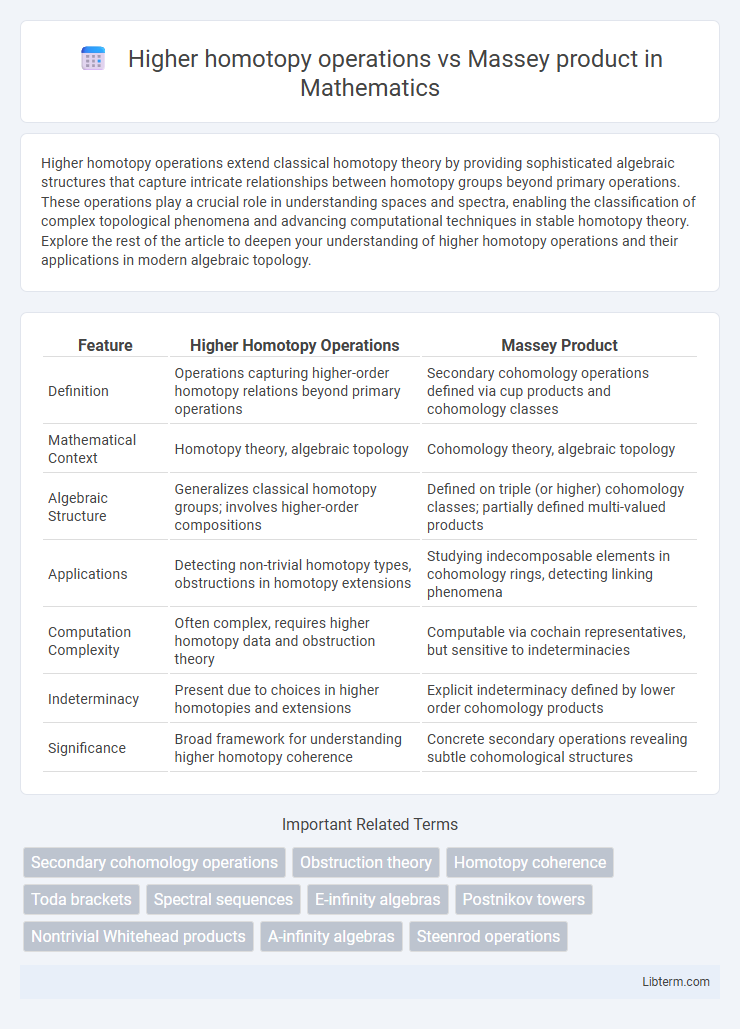
| Feature | Higher Homotopy Operations | Massey Product |
|---|---|---|
| Definition | Operations capturing higher-order homotopy relations beyond primary operations | Secondary cohomology operations defined via cup products and cohomology classes |
| Mathematical Context | Homotopy theory, algebraic topology | Cohomology theory, algebraic topology |
| Algebraic Structure | Generalizes classical homotopy groups; involves higher-order compositions | Defined on triple (or higher) cohomology classes; partially defined multi-valued products |
| Applications | Detecting non-trivial homotopy types, obstructions in homotopy extensions | Studying indecomposable elements in cohomology rings, detecting linking phenomena |
| Computation Complexity | Often complex, requires higher homotopy data and obstruction theory | Computable via cochain representatives, but sensitive to indeterminacies |
| Indeterminacy | Present due to choices in higher homotopies and extensions | Explicit indeterminacy defined by lower order cohomology products |
| Significance | Broad framework for understanding higher homotopy coherence | Concrete secondary operations revealing subtle cohomological structures |
Introduction to Higher Homotopy Operations
Higher homotopy operations extend classical algebraic topology tools by capturing obstructions to rectifying homotopy commutative diagrams beyond primary operations. Unlike Massey products, which detect specific secondary cohomology operations related to triple intersections, higher homotopy operations generalize this framework to arbitrary orders, organizing homotopy coherence data systematically. These operations provide refined invariants critical for studying complex spaces in homotopy theory, especially when analyzing iterated loop spaces and structured ring spectra.
Overview of Massey Products
Massey products are higher-order cohomology operations that generalize the cup product, capturing nontrivial interactions in the cohomology ring of a topological space. Defined using multi-valued operations on cohomology classes, they detect subtle algebraic structures that ordinary cohomology products cannot reveal. Massey products play a crucial role in distinguishing spaces with equivalent cohomology rings but different homotopy types, serving as fundamental tools in both algebraic topology and homotopy theory.
Historical Context and Development
Higher homotopy operations, emerging in the mid-20th century, extended classical tools in algebraic topology by capturing intricate relations in loop spaces beyond primary homotopy groups. The Massey product, introduced in the 1950s by William Massey, served as an early example of a higher-order cohomology operation detecting nontrivial linking phenomena absent in ordinary cup products. Both concepts evolved through collaborative advances in homotopy theory and cohomology, shaping modern understanding of complex algebraic and topological structures.
Algebraic Topology: Core Concepts
Higher homotopy operations extend classical Massey products by encoding intricate obstruction information in the homotopy groups of spaces beyond primary cohomological operations. Unlike Massey products, which arise from triple or multiple cup products in cohomology, higher homotopy operations capture nontrivial compositions in higher homotopy group contexts, reflecting deeper structural properties of topological spaces. These operations play a crucial role in distinguishing spaces with identical homology but different homotopy types, thereby enriching the algebraic topology toolkit for classifying and studying complex spaces.
Definitions and Fundamental Differences
Higher homotopy operations generalize primary homotopy invariants, capturing obstructions to extending partial homotopies in a homotopical setting, often encoded via higher-order structures such as Toda brackets. Massey products arise in cohomology theory as higher-order cohomological operations detecting nontrivial cup product relations beyond binary products, defined in terms of cochain-level data with indeterminacies. The fundamental difference lies in their domains and applications: higher homotopy operations operate within homotopy groups or spaces emphasizing obstruction theory, while Massey products focus on algebraic features of cohomology rings reflecting deeper structure in differential graded algebras.
Computational Methods for Each Operation
Higher homotopy operations and Massey products both serve as tools to detect intricate algebraic structures in homotopy theory, yet their computational methods differ significantly. Calculating higher homotopy operations often involves advanced obstruction theory and spectral sequence analysis, requiring detailed handling of simplicial resolutions or model categories. Conversely, Massey products are typically computed through cohomology class manipulations within differential graded algebras or via explicit chain-level representatives, making use of cup products and higher cochains to extract secondary and tertiary operations.
Applications in Homotopy Theory
Higher homotopy operations provide refined algebraic invariants in homotopy theory, enabling detailed classification of complex spaces beyond primary homotopy groups. Massey products serve as specific examples of higher-order cohomology operations that detect nontrivial linking phenomena in loop spaces and spectral sequences. Their applications include distinguishing between homotopy types, analyzing obstructions in fibration sequences, and informing the structure of differential graded algebras in stable homotopy theory.
Examples Illustrating Both Structures
Higher homotopy operations, such as Toda brackets, express indeterminacies in compositions of homotopy classes beyond primary levels and can detect more subtle algebraic structures in spaces. Massey products arise in the cohomology ring of a space, providing higher-order cohomological invariants indicating nontrivial linking of cycles, with classical examples seen in the cohomology of link complements or the Borromean rings. The triple Massey product in the cohomology of a wedge of spheres exemplifies Massey products, while the associated Toda brackets in the stable homotopy groups of spheres illustrate higher homotopy operations, highlighting their interplay in detecting nontrivial homotopy and cohomology interactions.
Comparative Advantages and Limitations
Higher homotopy operations provide a systematic framework to detect finer homotopical structures beyond classical invariants, offering greater flexibility and applicability in complex topological spaces compared to Massey products. Massey products, while more explicit and computationally accessible, are limited to specific cohomology classes and may fail to capture higher-order obstructions detectable by full higher homotopy operations. The trade-off lies in the balance between computational tractability of Massey products and the broader theoretical scope but increased complexity of higher homotopy operations.
Future Directions and Open Problems
Future directions in higher homotopy operations include developing computational tools for effectively handling complex compositions and extending algebraic models in homotopy theory. Open problems involve characterizing the full extent of interactions between higher homotopy operations and Massey products, particularly in non-formal spaces and their implications for detecting finer homotopical invariants. Investigating the role of these operations in derived algebraic geometry and stable homotopy theory remains a critical area for advancing theoretical understanding.
Higher homotopy operations Infographic
 libterm.com
libterm.com