Embedding transforms complex data into meaningful vector representations, enabling machines to understand and process information more effectively. This technique is crucial for improving search engines, recommendation systems, and natural language processing applications. Discover how embedding can enhance your technology by reading the full article.
Table of Comparison
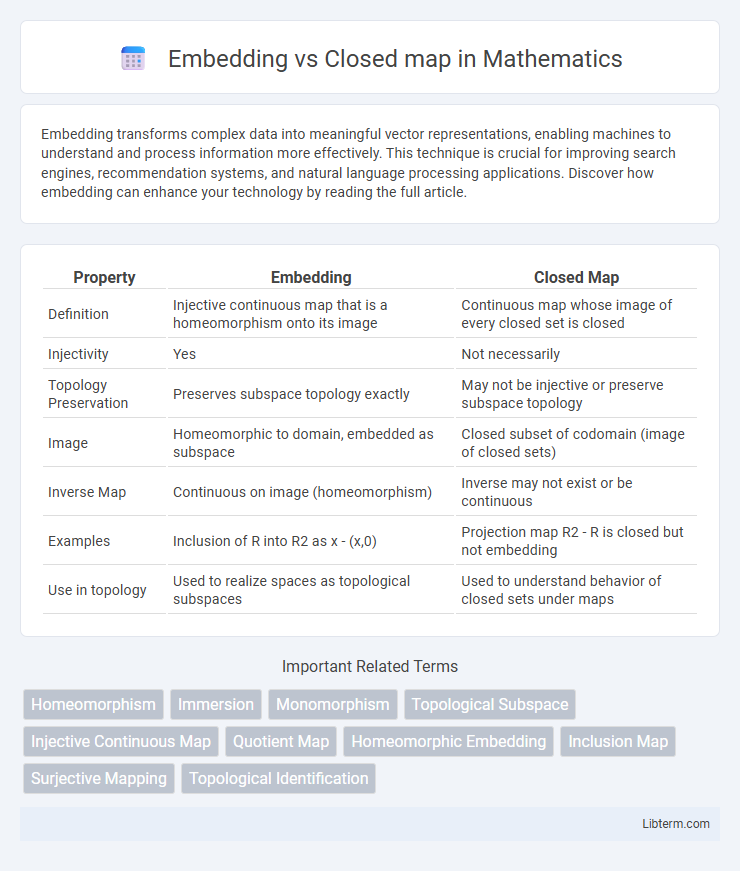
| Property | Embedding | Closed Map |
|---|---|---|
| Definition | Injective continuous map that is a homeomorphism onto its image | Continuous map whose image of every closed set is closed |
| Injectivity | Yes | Not necessarily |
| Topology Preservation | Preserves subspace topology exactly | May not be injective or preserve subspace topology |
| Image | Homeomorphic to domain, embedded as subspace | Closed subset of codomain (image of closed sets) |
| Inverse Map | Continuous on image (homeomorphism) | Inverse may not exist or be continuous |
| Examples | Inclusion of R into R2 as x - (x,0) | Projection map R2 - R is closed but not embedding |
| Use in topology | Used to realize spaces as topological subspaces | Used to understand behavior of closed sets under maps |
Introduction to Embedding and Closed Maps
Embedding is a type of function between topological spaces that preserves the structure by being both a homeomorphism onto its image and an injective continuous map. Closed maps, on the other hand, are functions where the image of every closed set is also closed, ensuring that key topological properties are maintained in the image space. Understanding embeddings helps analyze how spaces can be represented within others without losing their topological identity, while closed maps provide insight into how closedness is preserved under continuous mappings.
Defining Embedding in Topology
An embedding in topology is a homeomorphism onto its image, meaning it is a continuous injective map from one topological space into another that induces a subspace topology on the image. Unlike a closed map, which simply sends closed sets to closed sets, an embedding preserves both the topological structure and the distinction of points. Embeddings allow the original space to be viewed as a topological subspace of the target space, maintaining all open set relations and continuity properties.
Understanding Closed Maps
Closed maps are continuous functions between topological spaces that map closed sets to closed sets, ensuring the image retains topological closure properties. Unlike embeddings, which are injective and homeomorphic onto their images, closed maps may not be injective but preserve the structure of closed sets, playing a crucial role in quotient space constructions. Understanding closed maps is essential for analyzing how continuous maps affect closure properties and how they facilitate the study of topological invariants under image mappings.
Key Differences Between Embedding and Closed Maps
Embedding maps require the map to be both injective and homeomorphic onto its image, preserving topological properties such as continuity and openness. Closed maps, on the other hand, are defined by the property that the image of every closed set is closed, without necessarily preserving injectivity or being homeomorphic. The key distinction lies in embeddings maintaining a topological equivalence with their image, whereas closed maps focus solely on the structural property of closed sets under the mapping.
Mathematical Formulations and Examples
An embedding is a map \( f: X \to Y \) between topological spaces that is a homeomorphism onto its image, preserving topological structure and injectivity, characterized by the condition that \( f \) is continuous, injective, and \( f^{-1} \) on \( f(X) \) is also continuous. In contrast, a closed map \( g: X \to Y \) ensures the image of every closed set in \( X \) is closed in \( Y \), which does not require injectivity or preservation of topological equivalence. For example, the inclusion map \( i: [0,1) \to \mathbb{R} \) is an embedding since it is injective and continuous with a continuous inverse onto its image, whereas the projection map \( p: \mathbb{R}^2 \to \mathbb{R} \), defined by \( p(x,y) = x \), is a closed map as it sends closed sets to closed sets but is not an embedding.
Applications of Embedding in Mathematics
Embedding in mathematics is extensively applied in topology and geometry to represent one space within another while preserving structure, facilitating the visualization and analysis of complex spaces. In differential geometry, embeddings allow smooth manifolds to be studied as submanifolds of Euclidean spaces, aiding in curvature and shape analysis. Closed maps, unlike embeddings, are crucial in continuity and compactness arguments but do not necessarily preserve the intricate structural details essential for applications like manifold theory and algebraic topology.
Applications of Closed Maps in Real-world Scenarios
Closed maps enable robust topological applications such as continuous image processing and geographic information systems by preserving closed sets under mapping, which ensures stability in data transformations. They are crucial in functional analysis for defining quotient spaces and in differential geometry for analyzing manifolds, providing reliable structural integrity of spaces during mappings. These properties make closed maps indispensable in engineering fields for system modeling and in computer graphics for rendering closed shapes without gaps.
Advantages and Limitations of Embeddings
Embeddings provide a powerful advantage by converting complex data such as text, images, or graphs into dense vector representations, enabling efficient similarity search and machine learning integration. They excel in handling high-dimensional data and capturing semantic relationships, but their limitations include potential loss of interpretability and reliance on large, quality datasets for training. Compared to closed maps, embeddings offer more flexibility and scalability but may struggle with precise boundary definitions and sometimes require significant computational resources.
When to Use Closed Maps Over Embedding
Closed maps are preferred over embeddings when it is essential to preserve the topological structure and identity of the original space, especially in complex manifold mapping scenarios. They ensure that the image of a space is topologically closed, which helps maintain boundary behaviors and compactness essential for continuous function analysis. Closed maps are critical in algebraic topology and geometric analysis where embedding may distort or lose important topological features.
Summary: Choosing Between Embedding and Closed Maps
Choosing between embedding and closed maps depends on the topological properties and the desired level of continuity preservation in the mapping. Embeddings require a homeomorphism onto their image, preserving both structure and topology, while closed maps ensure that images of closed sets remain closed, which is crucial in compactness and separation properties. For applications needing a faithful topological representation of the domain, embeddings are preferred; closed maps are ideal when dealing with quotient spaces or ensuring image closure in target spaces.
Embedding Infographic
 libterm.com
libterm.com