Non-regular languages cannot be recognized by finite automata and often require more powerful computational models like pushdown automata or Turing machines. These languages exhibit complexities such as nested structures or counting, which finite automata cannot handle. Dive into the rest of this article to understand how non-regular languages impact computation and formal language theory.
Table of Comparison
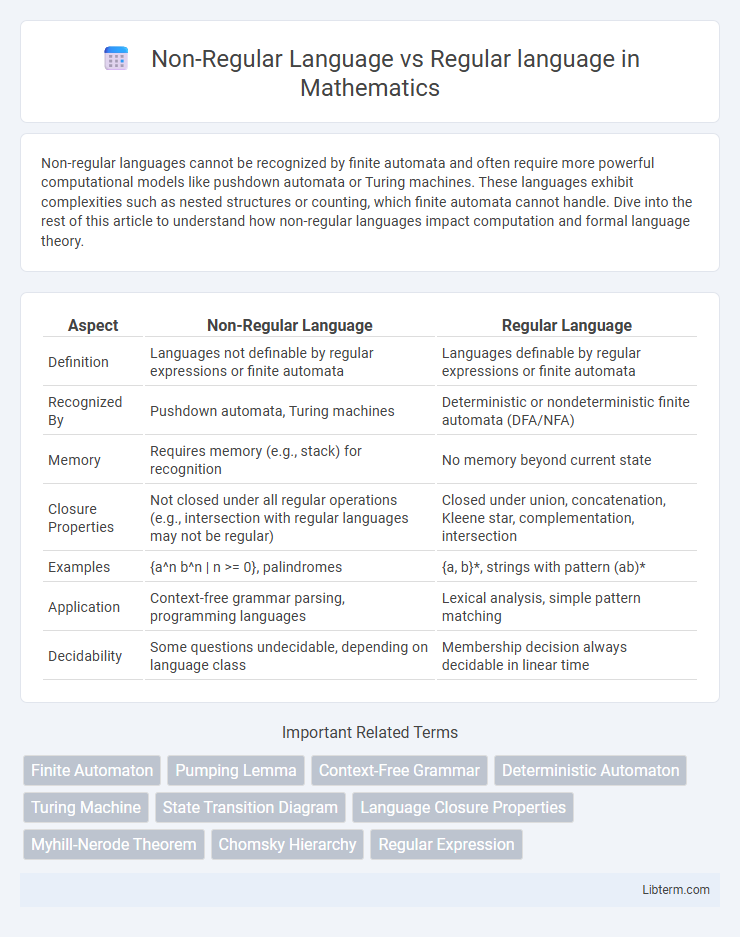
| Aspect | Non-Regular Language | Regular Language |
|---|---|---|
| Definition | Languages not definable by regular expressions or finite automata | Languages definable by regular expressions or finite automata |
| Recognized By | Pushdown automata, Turing machines | Deterministic or nondeterministic finite automata (DFA/NFA) |
| Memory | Requires memory (e.g., stack) for recognition | No memory beyond current state |
| Closure Properties | Not closed under all regular operations (e.g., intersection with regular languages may not be regular) | Closed under union, concatenation, Kleene star, complementation, intersection |
| Examples | {a^n b^n | n >= 0}, palindromes | {a, b}*, strings with pattern (ab)* |
| Application | Context-free grammar parsing, programming languages | Lexical analysis, simple pattern matching |
| Decidability | Some questions undecidable, depending on language class | Membership decision always decidable in linear time |
Introduction to Formal Languages
Non-regular languages cannot be represented by finite automata or regular expressions, distinguishing them from regular languages which are defined by these models. Formal language theory categorizes languages based on their complexity and the computational power required for recognition, with regular languages forming the simplest class. Understanding the difference between non-regular and regular languages is fundamental for automata theory and the design of parsers in compiler construction.
Defining Regular Languages
Regular languages are formal languages that can be expressed using regular expressions or recognized by finite automata, representing patterns with finite memory. Non-regular languages cannot be captured by finite automata, often requiring more powerful computational models like pushdown automata or Turing machines. The defining property of regular languages is their closure under operations such as union, concatenation, and Kleene star, enabling efficient pattern matching and computational simplicity.
Characteristics of Regular Languages
Regular languages are defined by their ability to be represented by finite automata, regular expressions, or deterministic context-free grammars, showcasing closure under operations such as union, concatenation, and Kleene star. They exhibit predictable computational complexity with membership testing achievable in linear time, contrasting non-regular languages which require more powerful computational models like pushdown automata. The limitations of regular languages include their inability to count or handle nested structures, making them inadequate for describing context-sensitive dependencies present in non-regular languages.
Defining Non-Regular Languages
Non-regular languages are formal languages that cannot be described by any finite automaton, meaning they lack a regular grammar or expression representation. These languages exhibit patterns requiring memory beyond finite states, such as balanced parentheses or equal numbers of certain symbols, which violate the pumping lemma for regular languages. Understanding non-regular languages is crucial in computational theory to distinguish the limitations of regular expressions and finite automata in language recognition.
Key Differences Between Regular and Non-Regular Languages
Regular languages can be described by finite automata and regular expressions, characterized by limited memory and closure under operations like union, intersection, and complementation. Non-regular languages require more powerful computational models such as pushdown automata or Turing machines, due to their ability to handle nested structures and infinite memory aspects. The key differences include decidability properties, closure under specific operations, and the class of languages each automaton can recognize efficiently.
Examples of Regular Languages
Regular languages include examples like the set of all strings over {a, b} containing an even number of a's, the language consisting of all strings that start with a specific prefix such as "abc," and the language containing all strings ending with a particular suffix like "01." These languages can be represented by regular expressions or finite automata, enabling efficient pattern matching and lexical analysis. In contrast, non-regular languages, such as the set of strings with equal numbers of a's and b's (e.g., {a^n b^n | n >= 0}), cannot be recognized by finite automata due to their requirement for potentially unbounded memory.
Examples of Non-Regular Languages
Non-regular languages include examples such as {a^n b^n | n >= 0}, where the number of a's must match the number of b's, a pattern that finite automata cannot recognize. Another example is the language {ww | w {a,b}*}, consisting of strings that are exactly repeated, requiring memory beyond regular language capabilities. These examples illustrate languages that require context-free or more powerful grammars, highlighting the limitations of regular languages and finite automata.
Techniques for Proving Non-Regularity
Pumping Lemma is a fundamental technique for proving non-regularity by demonstrating that all sufficiently long strings in the language cannot be decomposed to satisfy the lemma's conditions. Closure properties of regular languages, such as closure under union, intersection, and complement, are exploited to transform a non-regular problem into an equivalent problem whose language properties imply non-regularity. Myhill-Nerode Theorem provides an advanced tool for non-regularity proof by identifying the infinite number of equivalence classes in a language, which contradicts the finite state nature of regular languages.
Practical Applications of Regular and Non-Regular Languages
Regular languages are widely used in text processing, lexical analysis, and pattern matching due to their efficient recognition by finite automata and compatibility with regular expressions. Non-regular languages, characterized by nested or recursive structures, find practical applications in programming language syntax analysis, compiler design, and natural language processing, which require context-free or context-sensitive grammars for accurate parsing. The distinction between these language classes guides the choice of computational models, impacting the development of software tools and algorithms in formal language theory.
Conclusion: Importance in Theoretical Computer Science
Non-regular languages extend the computational boundaries beyond regular languages, highlighting the limitations of finite automata and showcasing the necessity for more powerful models like pushdown automata and Turing machines. Understanding the distinction between regular and non-regular languages is crucial for classifying problems based on their computational complexity and decidability. This classification underpins key results in formal language theory and automata, forming the foundation for compiler design, language processing, and complexity theory in theoretical computer science.
Non-Regular Language Infographic
 libterm.com
libterm.com