The Heaviside step function is a fundamental concept in mathematics and engineering, widely used to represent signals that switch on at a specific point in time. Its value is zero for negative inputs and one for positive inputs, making it essential in control theory and signal processing. Explore the rest of the article to understand how the Heaviside function applies to your work and its practical implementations.
Table of Comparison
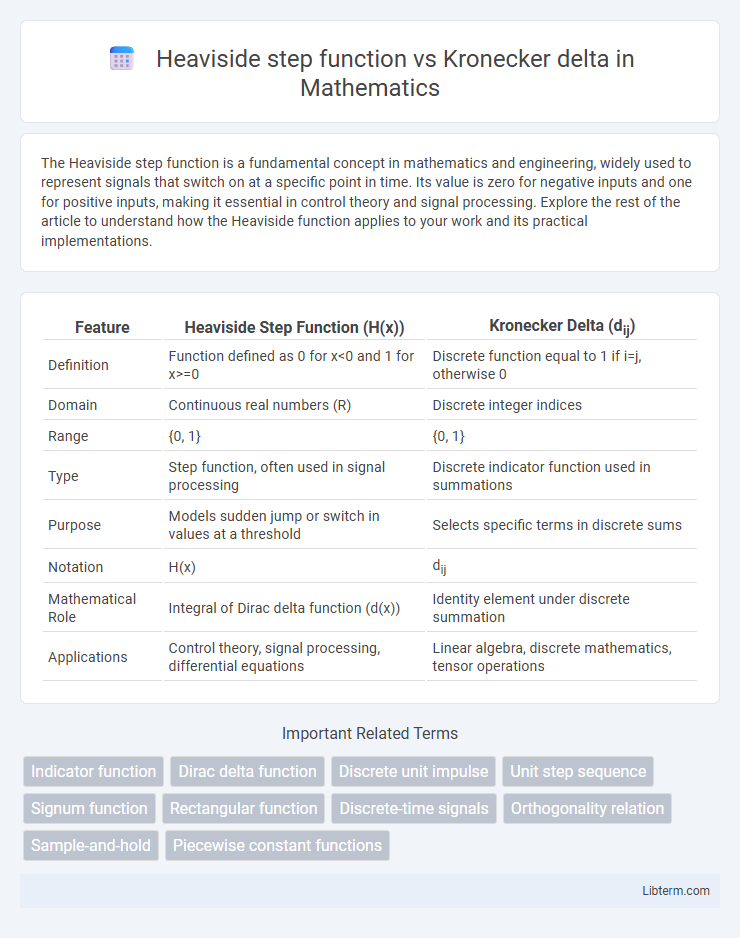
| Feature | Heaviside Step Function (H(x)) | Kronecker Delta (dij) |
|---|---|---|
| Definition | Function defined as 0 for x<0 and 1 for x>=0 | Discrete function equal to 1 if i=j, otherwise 0 |
| Domain | Continuous real numbers (R) | Discrete integer indices |
| Range | {0, 1} | {0, 1} |
| Type | Step function, often used in signal processing | Discrete indicator function used in summations |
| Purpose | Models sudden jump or switch in values at a threshold | Selects specific terms in discrete sums |
| Notation | H(x) | dij |
| Mathematical Role | Integral of Dirac delta function (d(x)) | Identity element under discrete summation |
| Applications | Control theory, signal processing, differential equations | Linear algebra, discrete mathematics, tensor operations |
Introduction to Heaviside Step Function and Kronecker Delta
The Heaviside step function is a discontinuous function defined as zero for negative inputs and one for positive inputs, commonly used in signal processing and differential equations to model switching behavior. The Kronecker delta is a discrete function equal to one when its indices are identical and zero otherwise, serving as an identity element in summations and matrix operations. Both functions are fundamental in mathematics and engineering, with the Heaviside step function representing continuous phenomena and the Kronecker delta handling discrete scenarios.
Mathematical Definitions
The Heaviside step function H(x) is defined as H(x) = 0 for x < 0 and H(x) = 1 for x >= 0, serving as a continuous unit step function often used in signal processing and differential equations. The Kronecker delta d_ij is defined as d_ij = 1 if i = j and d_ij = 0 if i j, acting as a discrete identity function primarily in summations and linear algebra. Both functions serve as fundamental mathematical tools representing binary conditions but differ in their domains--continuous for Heaviside and discrete for Kronecker delta.
Fundamental Properties
The Heaviside step function, H(x), is a discontinuous function valued at 0 for negative inputs and 1 for positive inputs, modeling signal activation and often used in control theory and differential equations. The Kronecker delta, d_ij, is a discrete function defined as 1 when indices i and j are equal and 0 otherwise, serving as an identity element in summations and matrix operations. Both functions exhibit fundamental properties of selection and indication, where Heaviside acts as a continuous threshold operator and Kronecker delta provides discrete identity correspondence.
Graphical Representation
The Heaviside step function graphically appears as a sudden jump from 0 to 1 at a specified point, typically 0, representing a continuous step shift. In contrast, the Kronecker delta is represented graphically as a discrete spike or impulse at a single point within a discrete domain, with values zero everywhere else. These visual distinctions highlight the Heaviside function's role in continuous systems and the Kronecker delta's use in discrete, summation-based contexts.
Discrete vs. Continuous Nature
The Heaviside step function is a continuous function used to represent a sudden change from zero to one at a specific point on the real number line, ideal for modeling continuous-time systems. In contrast, the Kronecker delta is a discrete function defined only at integer values, equaling one when indices are equal and zero otherwise, commonly applied in discrete-time signals and sequences. The key difference lies in their domains: Heaviside operates over continuous variables, while Kronecker delta functions over discrete indices.
Applications in Mathematics and Engineering
The Heaviside step function is widely used in engineering for modeling signal processing and system responses, especially in control theory and differential equations. The Kronecker delta serves as a key tool in discrete mathematics and digital signal processing, enabling the representation of orthogonal functions and simplifying summations in matrix operations. Both functions play crucial roles in solving boundary value problems, with the Heaviside function addressing continuous systems and the Kronecker delta applied in discrete system analysis.
Relationship Between the Functions
The Heaviside step function and the Kronecker delta serve distinct roles in signal processing and discrete mathematics, where the Heaviside function represents a unit step in continuous time, while the Kronecker delta acts as an identity element for discrete indices. The derivative of the Heaviside step function in the continuous domain corresponds to the Dirac delta function, which parallels the Kronecker delta in discrete settings by selecting specific points or values. This relationship highlights their complementary nature, with the Heaviside function serving as a cumulative sum operator and the Kronecker delta functioning as a discrete selector or indicator.
Usage in Signal Processing
The Heaviside step function is widely used in signal processing to represent signals that turn on at a specific time, modeling unit step responses and causal systems. The Kronecker delta serves as a discrete-time identity function crucial for sampling and digital signal analysis, acting as a discrete impulse in sequences. Both functions facilitate system behavior characterization, with the Heaviside step handling continuous-time signals and the Kronecker delta managing discrete-time signal operations.
Common Mistakes and Misconceptions
The Heaviside step function is frequently mistaken for the Kronecker delta, despite fundamentally differing as a continuous function used in signal processing versus a discrete function used in summation indices. Confusion often arises when users incorrectly apply the Kronecker delta in continuous-time systems or misinterpret the Heaviside function as zero everywhere except at a single point. Clarifying that the Kronecker delta equals one only when indices match, while the Heaviside step function transitions values across a threshold, helps avoid critical errors in mathematical modeling and analysis.
Summary and Key Differences
The Heaviside step function is a continuous function often used to represent a signal turning on at a certain point, defined as zero for negative inputs and one for positive inputs, including a specific value at zero. The Kronecker delta is a discrete function defined on integers, equaling one when its two indices are equal and zero otherwise, primarily used in summations and discrete systems. Key differences include the Heaviside function's role in continuous time signals and integrals versus the Kronecker delta's application in discrete mathematics and summations, reflecting their distinct domains and uses in signal processing and linear algebra.
Heaviside step function Infographic
 libterm.com
libterm.com