A sheaf is a bundle of grain stalks tied together after harvesting, traditionally used to facilitate drying and transport. Understanding the historical and agricultural significance of a sheaf can deepen your appreciation for farming practices and rural traditions. Explore the rest of the article to learn more about the cultural symbolism and practical uses of sheaves.
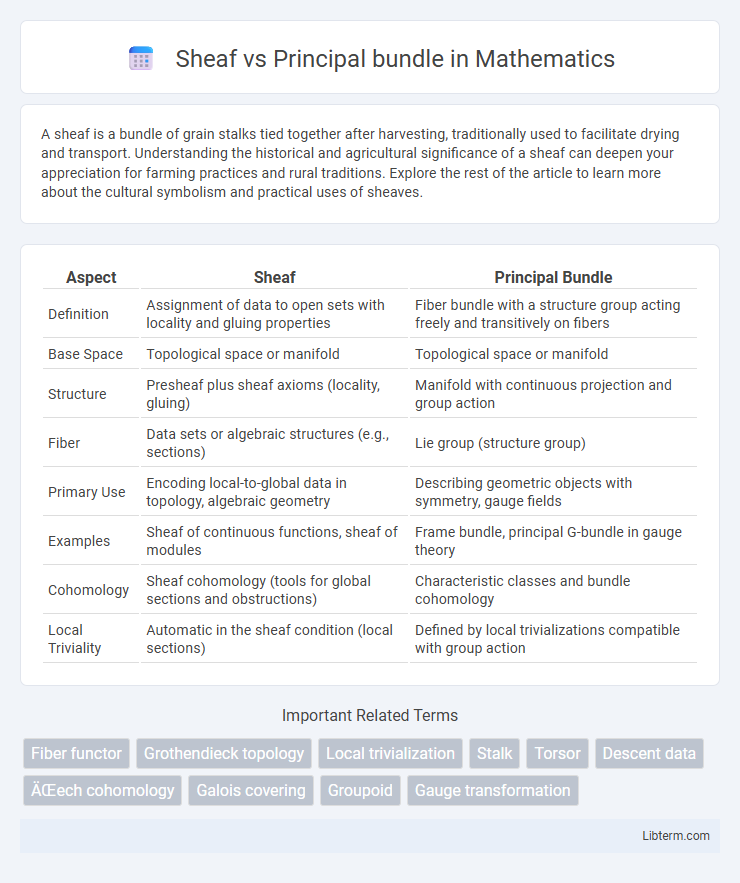
Table of Comparison
| Aspect | Sheaf | Principal Bundle |
|---|---|---|
| Definition | Assignment of data to open sets with locality and gluing properties | Fiber bundle with a structure group acting freely and transitively on fibers |
| Base Space | Topological space or manifold | Topological space or manifold |
| Structure | Presheaf plus sheaf axioms (locality, gluing) | Manifold with continuous projection and group action |
| Fiber | Data sets or algebraic structures (e.g., sections) | Lie group (structure group) |
| Primary Use | Encoding local-to-global data in topology, algebraic geometry | Describing geometric objects with symmetry, gauge fields |
| Examples | Sheaf of continuous functions, sheaf of modules | Frame bundle, principal G-bundle in gauge theory |
| Cohomology | Sheaf cohomology (tools for global sections and obstructions) | Characteristic classes and bundle cohomology |
| Local Triviality | Automatic in the sheaf condition (local sections) | Defined by local trivializations compatible with group action |
Introduction to Sheaves and Principal Bundles
Sheaves provide a framework to systematically track local data attached to open subsets of a topological space, enabling the reconstruction of global information through local consistency. Principal bundles, defined as fiber bundles with a continuous free action of a structure group acting transitively on the fibers, serve as fundamental objects in differential geometry for describing geometric structures and gauge fields. Both concepts are central to modern topology and geometry, with sheaves emphasizing local-to-global principles and principal bundles focusing on symmetry and group actions in fiber spaces.
Fundamental Concepts: Sheaf Theory
Sheaf theory provides a framework for systematically tracking local data attached to open subsets of a topological space and describing how this data coheres on overlapping regions. A sheaf assigns to each open set a set or algebraic structure, such as groups or rings, along with restriction maps that satisfy locality and gluing axioms essential for consistency. This formalism contrasts with principal bundles, which focus on globally defined fibered structures with a group action, while sheaves excel in encoding local-to-global properties fundamental in topology and algebraic geometry.
Principal Bundles: Definitions and Examples
Principal bundles are fiber bundles equipped with a continuous right action by a Lie group \(G\) that acts freely and transitively on each fiber, making the fiber isomorphic to the group \(G\) itself. A standard example is the frame bundle of a smooth manifold, where the structure group is the general linear group \(GL(n, \mathbb{R})\), and fibers consist of ordered bases for the tangent spaces. Principal bundles serve as the fundamental framework for gauge theories in physics, encapsulating concepts like connections and curvature within differential geometry.
Structural Differences Between Sheaves and Principal Bundles
Sheaves systematically assign algebraic or topological data to open sets of a space, emphasizing local-to-global consistency through stalks and restriction maps. Principal bundles consist of a total space with a continuous free action by a Lie group, encoding geometric twisting via transition functions that satisfy cocycle conditions. Unlike sheaves, principal bundles focus on global geometric structure and fiberwise symmetry, while sheaves prioritize local data coherence and gluing properties.
Mathematical Applications of Sheaves
Sheaves provide a versatile framework for systematically tracking local data and gluing conditions across topological spaces, making them essential in complex geometry, algebraic geometry, and cohomology theories. Unlike principal bundles, which model fiber spaces with a fixed structure group facilitating gauge theory and connection forms, sheaves enable the extension of local properties to global contexts through stalks and sections. This abstraction allows sheaves to unify diverse mathematical concepts such as solutions of differential equations, homological algebra, and moduli problems, driving advances in modern geometric and topological methods.
Role of Principal Bundles in Geometry and Physics
Principal bundles serve as fundamental geometric structures encoding symmetry and gauge data in fields such as differential geometry and theoretical physics. They provide a framework for describing fiber bundles with a continuous group action, crucial for formulating gauge theories, connections, and curvature on manifolds. Unlike sheaves, which organize local data into global sections, principal bundles directly model physical fields and symmetry transformations through their group-theoretic and topological properties.
Topological and Categorical Perspectives
A sheaf systematically encodes local data on a topological space, ensuring that these local sections can be uniquely glued together to form global sections, reflecting a fundamental locality principle in topology. Principal bundles, defined by a continuous action of a structure group on the total space with projection onto the base space, capture geometric and topological aspects of fiber bundles and gauge theories through their categorical structure as objects in the category of fiber bundles with group actions. From a categorical perspective, sheaves form a Grothendieck topos reflecting local-to-global properties, while principal bundles correspond to objects in groupoid categories or fibered categories, emphasizing their role in equivariant topology and descent theory.
Interrelations: Sheafification of Principal Bundles
Sheafification of principal bundles transforms the local data of a principal G-bundle into a sheaf of sections, encoding the bundle's geometric structure via a locally defined, compatible family of morphisms. This process facilitates the translation from topological principal bundles to sheaves of groups or sets, preserving the bundle's gluing and transition properties in a categorical context. Interrelations between sheaves and principal bundles enable advanced techniques in algebraic geometry and differential topology by studying principal bundles through their associated sheaves, which reflect local trivializations and equivariant maps.
Comparing Cohomology in Sheaf and Principal Bundle Contexts
Cohomology in sheaf theory captures local-to-global properties by systematically encoding sections of sheaves and their gluing conditions, providing powerful tools for algebraic and topological invariants. In contrast, cohomology associated with principal bundles often involves characteristic classes derived from curvature and connections, reflecting the geometric and topological features of the bundle structure. Comparing these approaches highlights that sheaf cohomology generalizes and unifies various cohomological methods, while principal bundle cohomology typically interprets these invariants in terms of fiber bundle geometry and gauge theory.
Frequently Asked Questions on Sheaves vs Principal Bundles
Sheaves and principal bundles serve distinct roles in geometry and topology; sheaves systematically record local data with gluing conditions, while principal bundles capture geometric structures with group actions and local trivializations. Frequently asked questions often address their differences in applications, such as sheaves being fundamental in cohomology theories and principal bundles in gauge theory and fiber bundle classification. Understanding how sheaves abstractly encode local-to-global principles contrasts with principal bundles' geometric emphasis on symmetry and connection is central to many inquiries.
Sheaf Infographic
 libterm.com
libterm.com