The hypergraph regularity lemma is a fundamental tool in combinatorics that extends Szemeredi's regularity lemma from graphs to hypergraphs, enabling the decomposition of complex hypergraphs into structured and pseudo-random parts. This lemma is pivotal for studying large-scale hypergraph properties and has applications in theoretical computer science, number theory, and discrete mathematics. Explore the rest of the article to understand how the hypergraph regularity lemma can enhance your grasp of advanced combinatorial structures.
Table of Comparison
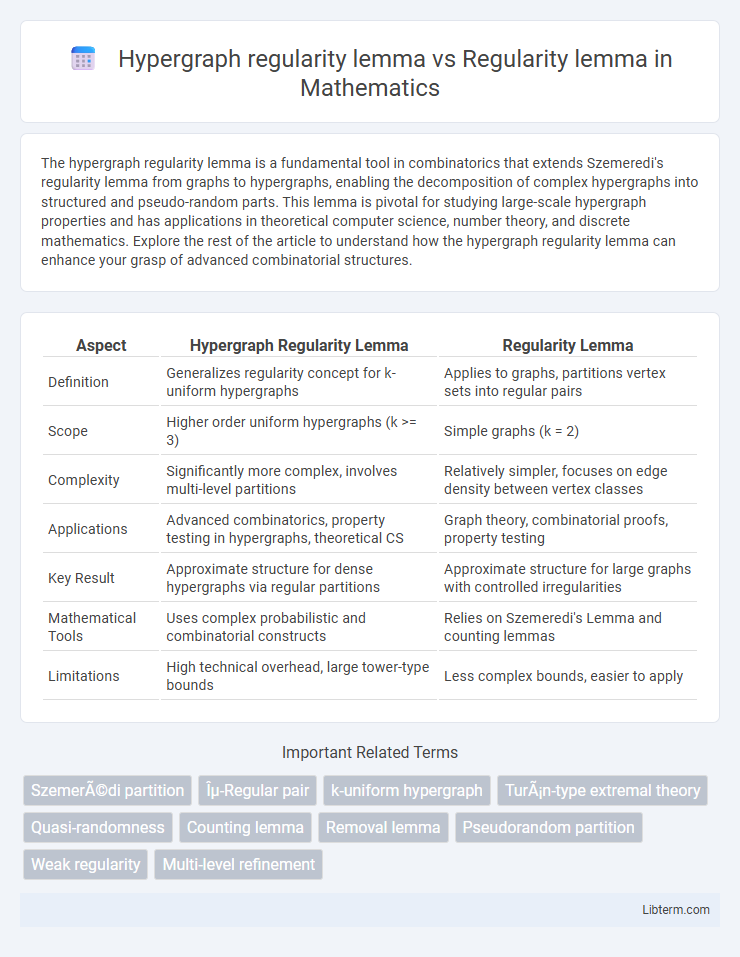
| Aspect | Hypergraph Regularity Lemma | Regularity Lemma |
|---|---|---|
| Definition | Generalizes regularity concept for k-uniform hypergraphs | Applies to graphs, partitions vertex sets into regular pairs |
| Scope | Higher order uniform hypergraphs (k >= 3) | Simple graphs (k = 2) |
| Complexity | Significantly more complex, involves multi-level partitions | Relatively simpler, focuses on edge density between vertex classes |
| Applications | Advanced combinatorics, property testing in hypergraphs, theoretical CS | Graph theory, combinatorial proofs, property testing |
| Key Result | Approximate structure for dense hypergraphs via regular partitions | Approximate structure for large graphs with controlled irregularities |
| Mathematical Tools | Uses complex probabilistic and combinatorial constructs | Relies on Szemeredi's Lemma and counting lemmas |
| Limitations | High technical overhead, large tower-type bounds | Less complex bounds, easier to apply |
Introduction to the Regularity Lemma
The Regularity Lemma, introduced by Endre Szemeredi, is a fundamental result in graph theory that approximates large graphs by a union of random-like bipartite graphs, facilitating the analysis of their structure. The Hypergraph Regularity Lemma extends this concept to hypergraphs, enabling decomposition into structured components despite their increased combinatorial complexity. These lemmas serve as crucial tools in extremal combinatorics, with the hypergraph version addressing challenges posed by multi-dimensional edges and more intricate interactions.
Overview of the Hypergraph Regularity Lemma
The Hypergraph Regularity Lemma generalizes the classical Regularity Lemma from graphs to hypergraphs, enabling the decomposition of hypergraphs into pseudorandom structures. This lemma addresses the complexity of higher-order interactions by partitioning vertices into clusters where hyperedges exhibit uniform densities, facilitating advanced combinatorial and probabilistic analysis. Its applications extend to areas such as property testing, extremal combinatorics, and theoretical computer science, providing powerful tools for understanding multidimensional network connectivity.
Historical Development and Milestones
The Regularity Lemma, introduced by Endre Szemeredi in 1975, marked a groundbreaking milestone in graph theory by providing a powerful tool for approximating large graphs with simpler structures via partitions into random-like subgraphs. The Hypergraph Regularity Lemma, developed in the 2000s by researchers including Nati Linial, Vojtech Rodl, and Yury G. Zarankievich, extended Szemeredi's framework to hypergraphs, addressing the complexity of multi-dimensional edges and enabling progress in hypergraph property testing and combinatorial number theory. Key milestones include Rodl and Schacht's refinement of the lemma for various hypergraph types and Gowers' work relating it to higher-order Fourier analysis, expanding the lemma's applicability in modern combinatorics.
Mathematical Foundations and Definitions
The Hypergraph Regularity Lemma generalizes the classic Regularity Lemma by extending its framework from simple graphs to k-uniform hypergraphs, incorporating higher-order combinatorial structures and complex partitioning schemes. While the Regularity Lemma describes a partition of a graph into a bounded number of vertex subsets where the bipartite graphs between parts are e-regular, the Hypergraph Regularity Lemma involves a hierarchy of partitions with uniformity conditions on multi-dimensional edge distributions to capture hyperedges' intricate interactions. Both lemmas rely on concepts of e-regularity and density but differ fundamentally in their mathematical definitions, with the hypergraph version requiring more sophisticated tools from combinatorics and measure theory to handle the increased complexity of hypergraph edges.
Key Differences Between Graph and Hypergraph Regularity Lemmas
The key differences between the graph regularity lemma and the hypergraph regularity lemma lie in complexity and structure: the graph regularity lemma deals with edges between pairs of vertices, producing a partition with regular pairs, while the hypergraph regularity lemma addresses higher-order edges among multiple vertices, requiring more intricate partitioning into regular hyperedges. Unlike graph partitions that are relatively straightforward, hypergraph regularity involves layered partitions and uniformity conditions to manage complex interactions across subsets of vertices. This complexity results in more elaborate definitions of regularity and increases the difficulty of applications in combinatorics and theoretical computer science.
Applications in Combinatorics and Theoretical Computer Science
The Hypergraph Regularity Lemma extends the classical Regularity Lemma by providing a framework to approximate complex hypergraph structures, enabling advanced analysis in higher-order combinatorial problems and multi-dimensional data sets. It is pivotal in proving results related to hypergraph versions of Szemeredi's theorem and facilitates property testing, algorithmic design, and complexity classification in theoretical computer science. Compared to the traditional Regularity Lemma, which primarily addresses graph partitioning and combinatorial optimization, the hypergraph variant allows for deeper insights into uniformity and structure in multi-relational data essential for modern combinatorics and computational complexity theory.
Challenges and Limitations in Hypergraph Regularity
Hypergraph regularity lemma faces significant challenges due to the complexity of hyperedges involving multiple vertices, leading to intricate combinatorial structures that are difficult to partition effectively. The limitations include enormous bounds on partition sizes, making the lemma less practical for large hypergraphs compared to the graph regularity lemma. Moreover, verifying regularity and applying counting lemmas in hypergraphs involve higher-dimensional intricacies, complicating both theoretical analysis and algorithmic applications.
Notable Proof Techniques and Strategies
The Hypergraph Regularity Lemma employs iterative partitioning and complex combinatorial frameworks to handle higher-order interactions beyond pairwise edges, leveraging techniques like multi-layered energy increment arguments and counting lemmas tailored for hypergraphs. In contrast, the classical Regularity Lemma relies on Szemeredi's partition method, using bipartite graphs and density calculations with a simpler energy increment strategy based on edge distributions. Notable proof strategies for hypergraph regularity include recursive decomposition and the use of hypergraph containers, which manage the combinatorial explosion inherent in hypergraph structures more effectively than traditional graph-based approaches.
Extensions and Recent Advances
The Hypergraph Regularity Lemma extends the classical Regularity Lemma by addressing k-uniform hypergraphs, enabling the decomposition of complex higher-order structures beyond simple graphs. Recent advances include refined counting lemmas and algorithmic improvements, which enhance the applicability of hypergraph regularity in combinatorics and theoretical computer science. These developments facilitate deeper insights into multi-dimensional patterns, enabling breakthroughs in problems related to property testing and arithmetic combinatorics.
Open Problems and Future Research Directions
The Hypergraph Regularity Lemma extends the classical Regularity Lemma by handling higher-order structures, but its complexity and bounds remain a critical open problem in combinatorics. Future research focuses on improving these bounds and developing efficient algorithms for hypergraph partitioning that preserve structural properties. Another key direction involves exploring applications in theoretical computer science, particularly in property testing and probabilistic combinatorics.
Hypergraph regularity lemma Infographic
 libterm.com
libterm.com