Completion helps in understanding the structure of algebraic or topological objects by filling in missing elements, while compactification deals with adding points to make a space compact without altering its essential properties. Extension allows the broadening of these structures to larger contexts, localization focuses on zooming in on specific parts or properties, and filtration provides a layered approach to analyze complexity step by step. Explore the rest of the article to deepen your insight into how these concepts interconnect and apply in various mathematical fields.
Table of Comparison
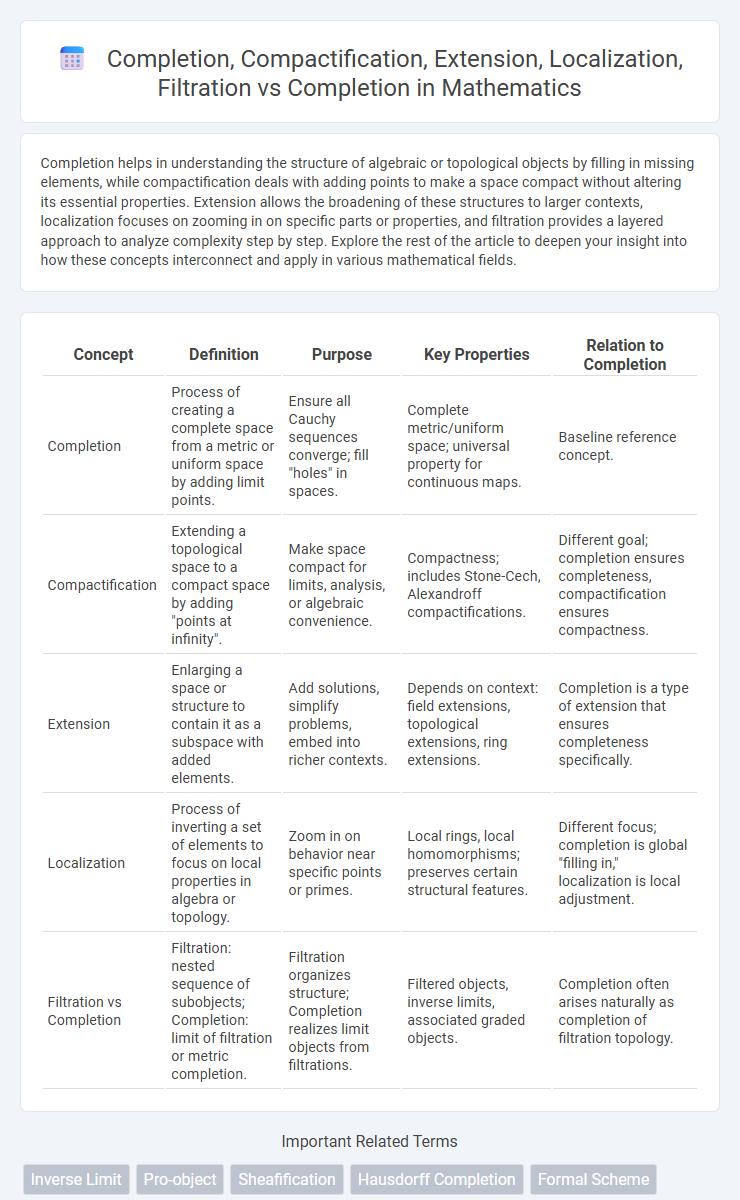
| Concept | Definition | Purpose | Key Properties | Relation to Completion |
|---|---|---|---|---|
| Completion | Process of creating a complete space from a metric or uniform space by adding limit points. | Ensure all Cauchy sequences converge; fill "holes" in spaces. | Complete metric/uniform space; universal property for continuous maps. | Baseline reference concept. |
| Compactification | Extending a topological space to a compact space by adding "points at infinity". | Make space compact for limits, analysis, or algebraic convenience. | Compactness; includes Stone-Cech, Alexandroff compactifications. | Different goal; completion ensures completeness, compactification ensures compactness. |
| Extension | Enlarging a space or structure to contain it as a subspace with added elements. | Add solutions, simplify problems, embed into richer contexts. | Depends on context: field extensions, topological extensions, ring extensions. | Completion is a type of extension that ensures completeness specifically. |
| Localization | Process of inverting a set of elements to focus on local properties in algebra or topology. | Zoom in on behavior near specific points or primes. | Local rings, local homomorphisms; preserves certain structural features. | Different focus; completion is global "filling in," localization is local adjustment. |
| Filtration vs Completion | Filtration: nested sequence of subobjects; Completion: limit of filtration or metric completion. | Filtration organizes structure; Completion realizes limit objects from filtrations. | Filtered objects, inverse limits, associated graded objects. | Completion often arises naturally as completion of filtration topology. |
Introduction to Completion in Mathematics
Completion in mathematics involves constructing a complete space by filling in "gaps" or limits of Cauchy sequences, often applied in metric spaces and rings. It extends an original structure into a dense, complete one, ensuring all limit points exist within the space, crucial in topology and algebra. This process contrasts with compactification, which bounds a space, and filtration, which organizes elements by layers, highlighting completion's role in achieving completeness through limits and convergence.
Understanding Compactification Methods
Compactification methods transform non-compact spaces into compact ones by adding limit points or boundaries, enhancing topological and geometric analysis. Completion involves creating a complete space by including limit points of Cauchy sequences, often used in metric and normed spaces. Extensions expand a given structure while preserving existing properties, and localization adjusts objects to focus on particular subsets or local behavior, whereas filtration filters a structure through nested subsets, providing layered insight that contrasts with completion's approach.
The Concept of Extension in Algebra and Topology
Extension in algebra and topology involves enlarging a given structure to a more comprehensive system that preserves original properties while enabling new operations or insights. In algebra, this may mean extending fields or modules to include solutions to equations or adding limits, while in topology, it often refers to extending spaces or functions to their closures or compactifications. Unlike completion, which focuses on filling in limits to make spaces complete or filtered objects separated, extension broadens the scope of the original object without necessarily imposing completeness or compactness.
Localization: Making Structures Local
Localization transforms algebraic structures by inverting a specified subset of elements, creating a localized ring or module that emphasizes local properties while preserving original operations. Unlike completion, which builds limits to "fill in" structures and filtrations that stratify objects via substructures, localization selectively refines focus to neighborhoods of interest, facilitating analysis of prime ideals and local behavior. This process extends structures without compactification or extension by appending inverses, crucial in algebraic geometry and number theory for examining properties at specific points or multiplicative sets.
Comparing Filtration and Completion
Filtration is a process that organizes a mathematical object into a nested sequence of subobjects, providing a layered structure that reflects complexity or size, while completion involves taking limits to fill in "gaps" and create a complete object with respect to a given filtration or topology. Completion can be viewed as the formal limit of the filtration steps, often resulting in enhanced analytical properties such as completeness and compactness. Unlike completion, which produces a new enriched object, filtration serves as the foundational decomposition that guides the completion process and helps analyze algebraic or topological structures through successive approximations.
Key Differences: Filtration vs Completion
Filtration organizes algebraic structures into a nested sequence of substructures, enabling analysis through successive approximations, while completion constructs a limit object that fills in gaps, producing a complete and often more manageable entity. Filtration provides a graded or filtered structure revealing internal layers, whereas completion emphasizes convergence and closure properties within a given topology or metric. The key difference lies in filtration being a preparatory step that highlights structure, whereas completion is a process that generates an enriched or fully completed object from that filtration.
Applications of Completion and Compactification
Completion techniques in algebra and topology facilitate solving equations and defining limits by filling in gaps within structures such as metric spaces, rings, and modules, enabling precise approximations in number theory and algebraic geometry. Compactification extends a non-compact space into a compact one, crucial in analysis and differential geometry for ensuring the existence of limits and extending functions continuously over boundaries, as seen in projective space and Stone-Cech compactification applications. These processes enhance computational methods and topological analysis, with completion supporting formal power series expansions and compactification providing frameworks for studying asymptotic behaviors and boundary phenomena.
Extensions and Localizations in Algebraic Structures
Extensions in algebraic structures involve expanding a given structure by adjoining new elements or operations while preserving its original properties, often realized through field extensions or module enlargements. Localization focuses on inverting specific elements or subsets within the structure to form localized rings or modules, enabling the study of properties localized at prime ideals or multiplicative sets. These processes contrast with completion, which fills in limits related to filtrations or topologies, and compactification, which adds boundary points to geometric objects, while filtrations provide a hierarchical decomposition refining structures prior to completion.
Real-World Examples of Compactification and Completion
Completion transforms a mathematical structure into a complete one by filling in missing limit points, as seen in the real numbers \(\mathbb{R}\) completing the rationals \(\mathbb{Q}\) with respect to the usual metric. Compactification involves embedding a non-compact space into a compact space, exemplified by the Stone-Cech compactification that adds "ideal points" to spaces like the natural numbers \(\mathbb{N}\) to ensure compactness. In real-world scenarios, completion models processes such as digital signal sampling where continuous signals are approximated by discrete sets, while compactification techniques apply in cosmology to model the universe with finite but boundary-less structures.
Conclusion: Interconnections among Completion, Compactification, Extension, and Localization
Completion, compactification, extension, and localization are deeply interrelated concepts in algebra and topology, each facilitating the study of structures by refining or enlarging them under controlled conditions. Completion often serves as a foundational step enabling compactification and extension by providing limit objects that retain essential properties, while localization adjusts structures to focus on specific parts or features, complementing the global perspectives gained through compactification. Together, these processes form a cohesive framework that enhances understanding by balancing local and global insights, filtering complex data through completion and filtration techniques to reveal intrinsic algebraic or topological characteristics.
Completion, Compactification, Extension, Localization, Filtration Infographic
 libterm.com
libterm.com