Partition is a crucial concept in computer science and data management, involving the division of data or processes into distinct parts for improved efficiency and organization. Understanding partitioning can enhance your system's performance by reducing complexity and enabling parallel processing. Discover the various types and applications of partitioning in the rest of this article.
Table of Comparison
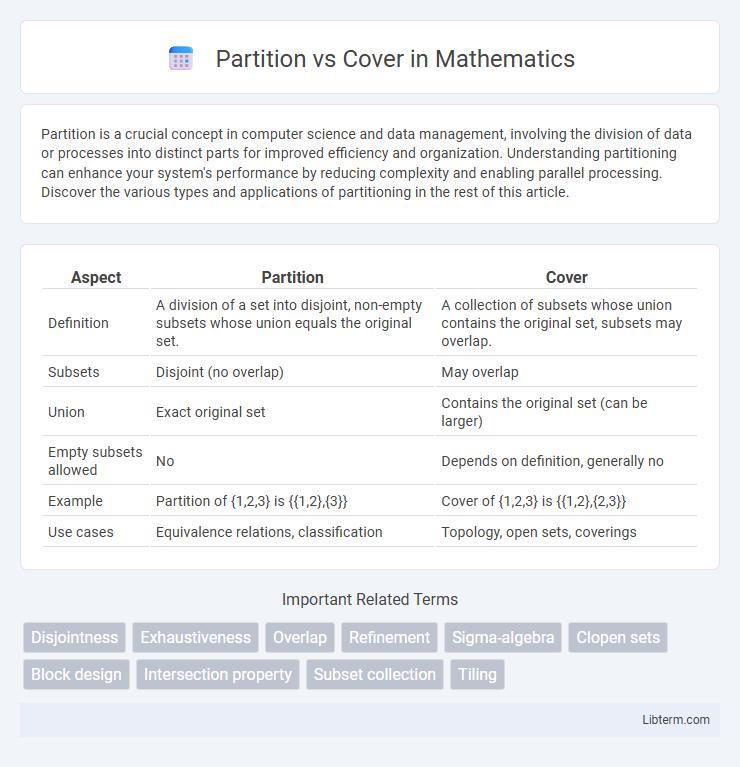
| Aspect | Partition | Cover |
|---|---|---|
| Definition | A division of a set into disjoint, non-empty subsets whose union equals the original set. | A collection of subsets whose union contains the original set, subsets may overlap. |
| Subsets | Disjoint (no overlap) | May overlap |
| Union | Exact original set | Contains the original set (can be larger) |
| Empty subsets allowed | No | Depends on definition, generally no |
| Example | Partition of {1,2,3} is {{1,2},{3}} | Cover of {1,2,3} is {{1,2},{2,3}} |
| Use cases | Equivalence relations, classification | Topology, open sets, coverings |
Understanding Partition and Cover in Mathematics
In mathematics, a partition of a set is a collection of non-empty, mutually disjoint subsets whose union equals the original set, ensuring every element belongs to exactly one subset. A cover, however, is a collection of subsets whose union contains the original set but allows overlaps and does not require every element to be in only one subset. Understanding the distinction between partition and cover is crucial for analyzing structures in set theory, topology, and combinatorics, where partitions enforce exclusivity while covers provide flexible inclusivity.
Fundamental Definitions: Partition vs Cover
A partition of a set divides the set into mutually exclusive and collectively exhaustive subsets, where each element belongs to exactly one subset, ensuring no overlap or omission. A cover, in contrast, is a collection of subsets whose union contains the entire set but allows for overlapping subsets and elements belonging to multiple subsets. Fundamentally, partitions impose strict exclusivity and completeness conditions, while covers prioritize coverage without exclusivity.
Key Differences Between Partition and Cover
Partition divides a set into disjoint subsets whose union equals the original set, ensuring no overlap between subsets. Cover consists of subsets whose union contains the original set but allows overlap among subsets and may include elements outside the original set. Key differences include exclusivity of subsets in partitions versus potential overlap in covers, and partitions require exact coverage of the set, while covers provide a superset coverage.
Visual Representation of Partitions and Covers
Partitions visually represent a set divided into disjoint subsets where each element belongs to exactly one subset, often illustrated by non-overlapping, distinct regions or blocks. Covers depict collections of subsets whose union contains the entire set, allowing overlap among subsets and resulting in overlapping shapes or regions in diagrams. This visual distinction highlights the exclusivity of partitions versus the inclusive, potentially overlapping nature of covers.
Properties of Partitions
Partitions of a set are collections of non-empty, mutually disjoint subsets whose union equals the original set, ensuring every element belongs to exactly one subset. Each subset in a partition is called a block or cell, and the partition is characterized by the properties of disjointness and completeness. Unlike covers, which can have overlapping subsets and do not require all elements to be included uniquely, partitions enforce a strict, mutually exclusive organization of the set elements.
Characteristics of Covers
Covers in set theory consist of a collection of subsets whose union includes the entire original set, allowing overlaps among these subsets. Each element of the original set belongs to at least one subset in the cover, but unlike partitions, subsets in a cover need not be mutually exclusive or collectively exhaustive without intersection. This flexibility makes covers suitable for applications requiring overlapping regions or distributed representations, such as topological spaces or data clustering.
Real-World Applications of Partition and Cover
Partitioning divides a set into exclusive, non-overlapping subsets, widely used in resource allocation for cloud computing and database sharding to optimize performance and scalability. Covering involves overlapping subsets that collectively include all elements, essential in network design for ensuring redundancy and fault tolerance across communication nodes. Real-world applications leverage partitions for task scheduling in operating systems, while covers support sensor network coverage and image segmentation in computer vision.
Advantages and Limitations of Partition and Cover
Partitions provide a clear and non-overlapping classification of a set, ensuring that each element belongs to exactly one subset, which simplifies analysis and avoids ambiguity in data segmentation. However, partitions may be too rigid for complex scenarios where elements exhibit overlapping characteristics, limiting their flexibility in modeling real-world phenomena. Covers allow subsets to overlap, capturing nuanced relationships and multiple memberships, but this can introduce ambiguity and complicate computations due to elements belonging to multiple subsets simultaneously.
Common Mistakes When Distinguishing Partition from Cover
Common mistakes when distinguishing partition from cover include assuming all covers are partitions, ignoring that partitions require mutually exclusive and collectively exhaustive subsets while covers only need to collectively cover the set. Overlapping subsets in covers often cause confusion, as partitions strictly prohibit overlaps. Misinterpreting the necessity for subsets to be nonempty in partitions leads to incorrect classifications and errors in set theory applications.
Summary: Choosing Between Partition and Cover
Partition divides a set into exclusive, non-overlapping subsets, ensuring each element belongs to exactly one subset, which optimizes clarity for strict categorization tasks. Cover allows subsets to overlap, enabling flexible groupings where elements can be shared, ideal for complex or multi-faceted data relationships. Selecting between partition and cover depends on the need for exclusivity versus overlap, balancing precision with representational flexibility in data analysis.
Partition Infographic
 libterm.com
libterm.com