Counting measure assigns values by counting the number of elements in a set, making it a fundamental concept in measure theory and probability. It plays a crucial role in defining integrals over discrete spaces and helps quantify the size of finite or countably infinite sets. Explore the rest of this article to deepen your understanding of how the counting measure applies to various mathematical contexts.
Table of Comparison
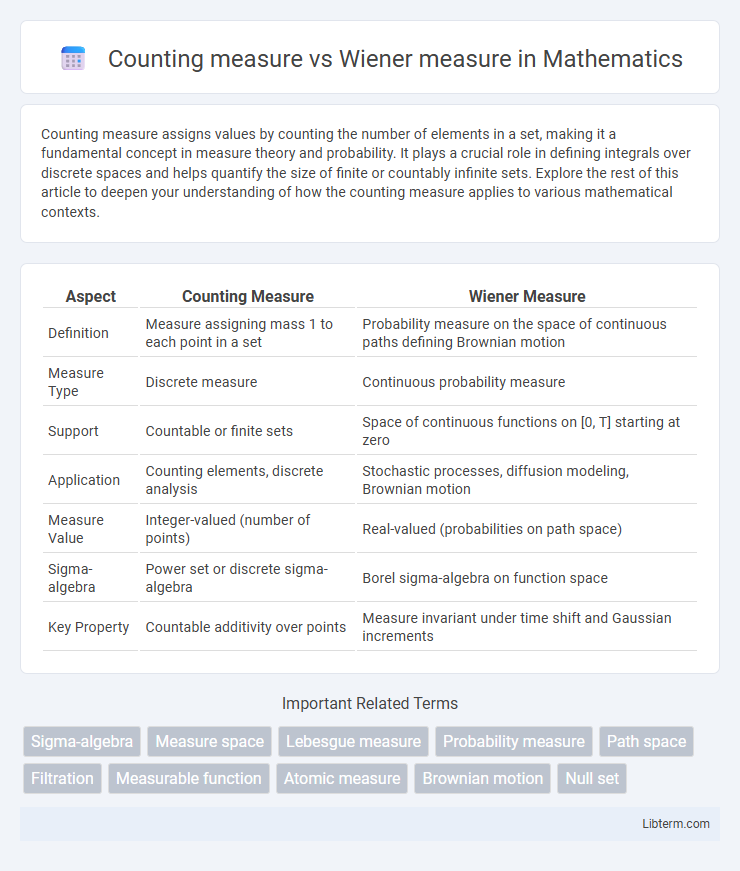
| Aspect | Counting Measure | Wiener Measure |
|---|---|---|
| Definition | Measure assigning mass 1 to each point in a set | Probability measure on the space of continuous paths defining Brownian motion |
| Measure Type | Discrete measure | Continuous probability measure |
| Support | Countable or finite sets | Space of continuous functions on [0, T] starting at zero |
| Application | Counting elements, discrete analysis | Stochastic processes, diffusion modeling, Brownian motion |
| Measure Value | Integer-valued (number of points) | Real-valued (probabilities on path space) |
| Sigma-algebra | Power set or discrete sigma-algebra | Borel sigma-algebra on function space |
| Key Property | Countable additivity over points | Measure invariant under time shift and Gaussian increments |
Introduction to Counting Measure and Wiener Measure
Counting measure assigns a value equal to the cardinality of a set, making it fundamental in discrete measure theory and combinatorial analysis. Wiener measure, rooted in probability theory, defines a measure on the space of continuous functions, specifically characterizing Brownian motion paths. Both measures serve as foundational tools in their respective domains, with counting measure applicable in discrete settings and Wiener measure crucial for stochastic processes.
Fundamental Concepts of Measure Theory
Counting measure assigns a measure equal to the number of elements in a set, making it discrete and straightforward, ideal for finite or countable spaces. Wiener measure models the probability distribution of continuous Brownian motion paths, essential in stochastic processes and functional analysis. Both measures exemplify fundamental concepts of measure theory: sigma-algebras, measure spaces, and integration, highlighting the difference between discrete and continuous frameworks.
Definition and Properties of Counting Measure
Counting measure assigns to each subset of a given set the number of elements it contains, making it a discrete and sigma-finite measure where every singleton has measure one. It is defined on all subsets, providing a direct way to measure size in countable sets, and is additive over disjoint unions. Unlike Wiener measure, which models continuous stochastic processes on function spaces, counting measure is purely combinatorial and non-probabilistic in nature.
Definition and Properties of Wiener Measure
The Wiener measure is a probability measure on the space of continuous functions, specifically modeling Brownian motion paths, assigning probabilities to sets of functions based on their path behaviors. Unlike the counting measure, which simply counts elements in discrete sets, the Wiener measure captures the intricate properties of continuous stochastic processes, such as Gaussian increments, almost sure continuity, and non-differentiability of paths. Its key properties include measure invariance under time shifts, the Markov property, and the ability to generate a complete separable metric probability space for stochastic analysis.
Key Differences Between Counting and Wiener Measures
Counting measure assigns a measure equal to the number of elements in a set, primarily used for discrete spaces and ensuring straightforward summation over finite or countable collections. Wiener measure, in contrast, is a probability measure on the space of continuous paths, fundamental in modeling Brownian motion with properties such as non-atomicity and path continuity. Key differences include the discrete vs. continuous nature of their domains, the counting measure's direct cardinality interpretation versus the Wiener measure's role in stochastic process theory, and their distinct applications in pure counting problems versus probabilistic modeling of diffusion processes.
Applications of Counting Measure in Mathematics
Counting measure plays a critical role in discrete mathematics, combinatorics, and number theory by assigning a measure equal to the cardinality of a set, facilitating the analysis of finite or countable structures. It is extensively used in probability theory for discrete probability spaces, enabling straightforward computation of probabilities by counting favorable outcomes. In contrast, Wiener measure is fundamental in stochastic processes, particularly Brownian motion, where it provides a continuous probability measure on function spaces rather than discrete sets.
Wiener Measure in Stochastic Processes
Wiener measure is a fundamental probability measure used in the study of stochastic processes, particularly Brownian motion, where it assigns probabilities to paths in the space of continuous functions. Unlike counting measure, which simply counts the number of elements in a set, Wiener measure provides a rigorous framework to analyze random continuous trajectories with the properties of independent, normally distributed increments. This measure plays a critical role in stochastic calculus, enabling the formulation and solution of stochastic differential equations and underpinning the theory of continuous-time martingales.
Comparison: Discreteness vs. Continuity
The counting measure assigns a discrete value to each individual element within a set, making it suitable for analyzing finite or countable spaces. In contrast, the Wiener measure is a continuous probability measure on the space of real-valued continuous functions, particularly used in modeling Brownian motion. This fundamental difference highlights the counting measure's role in discrete frameworks and the Wiener measure's application in continuous stochastic processes.
Importance in Probability Theory and Analysis
Counting measure assigns equal weight to each element in a discrete set, serving as a fundamental tool in combinatorics and discrete probability. Wiener measure underpins the rigorous mathematical description of Brownian motion, playing a crucial role in stochastic calculus and continuous-time probability theory. The interplay between these measures facilitates the analysis of both discrete and continuous stochastic processes, highlighting their importance in probability theory and harmonic analysis.
Conclusion: Selecting the Appropriate Measure
Selecting the appropriate measure depends on the nature of the underlying space and the problem context: the counting measure is ideal for discrete spaces with countable sets, ensuring each element is assigned measure one, while the Wiener measure is essential for modeling continuous stochastic processes like Brownian motion, capturing path-dependent probabilities. In applications requiring analysis of random paths, the Wiener measure offers a robust framework due to its foundation in continuous probability measures and Gaussian distributions. Understanding the distinct characteristics and domains of these measures allows for accurate modeling and analysis in probability theory and stochastic processes.
Counting measure Infographic
 libterm.com
libterm.com