Limitations define the boundaries within which processes or actions can occur, ensuring safety, efficiency, and compliance with regulations. Understanding your limits helps optimize performance and avoid potential risks in various contexts, from technology to personal development. Explore the full article to discover how setting and respecting limits can enhance your success and well-being.
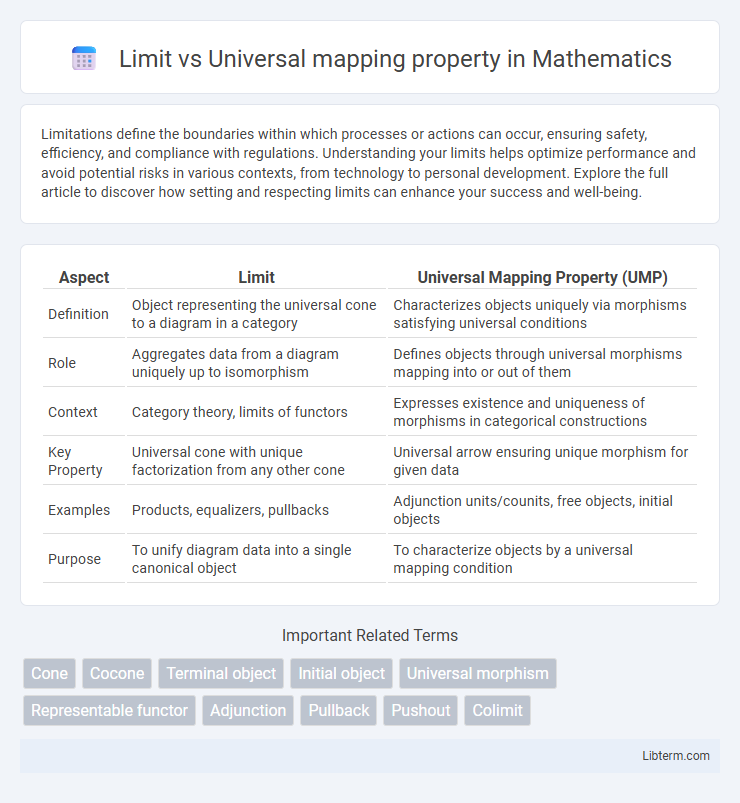
Table of Comparison
| Aspect | Limit | Universal Mapping Property (UMP) |
|---|---|---|
| Definition | Object representing the universal cone to a diagram in a category | Characterizes objects uniquely via morphisms satisfying universal conditions |
| Role | Aggregates data from a diagram uniquely up to isomorphism | Defines objects through universal morphisms mapping into or out of them |
| Context | Category theory, limits of functors | Expresses existence and uniqueness of morphisms in categorical constructions |
| Key Property | Universal cone with unique factorization from any other cone | Universal arrow ensuring unique morphism for given data |
| Examples | Products, equalizers, pullbacks | Adjunction units/counits, free objects, initial objects |
| Purpose | To unify diagram data into a single canonical object | To characterize objects by a universal mapping condition |
Introduction to Limits and Universal Mapping Properties
Limits in category theory provide a way to capture the universal solution to a diagram, representing objects and morphisms that factor uniquely through a limiting cone. Universal mapping properties characterize these limits by ensuring the existence of a unique morphism from any other cone into the limit object. This framework unifies constructions such as products, pullbacks, and inverse limits by leveraging their defining universal properties.
Defining Limits in Category Theory
Defining limits in category theory involves identifying a universal cone that factors uniquely through any other cone over a diagram, capturing the essence of universal mapping properties. Limits serve as a specific instance of universal properties, representing the most general solution to a given problem by formalizing the notion of compatibility and uniqueness in morphisms. This universal characterization enables the construction of objects like products, equalizers, and pullbacks by ensuring a unique factorization through the limit object.
Understanding the Universal Mapping Property (UMP)
The Universal Mapping Property (UMP) characterizes limits in category theory by specifying a unique morphism from any object to the limit object that factors through a given diagram. This property ensures that the limit serves as a universal solution, capturing all cones over the diagram in a canonical way. Understanding UMP is essential for recognizing limits as objects that represent natural transformations or commutative cones in a universal manner.
The Relationship Between Limits and UMP
Limits in category theory are characterized by their universal mapping property (UMP), which ensures a unique morphism exists from any other cone to the limit object. This UMP defines limits as terminal objects in the category of cones over a diagram, establishing a canonical factorization through the limit. Consequently, the concept of limits is intrinsically tied to the UMP, providing a universal characterization that encapsulates the essential mapping behavior of limits within categories.
Examples of Limits via UMP
The limit of a diagram in category theory can be understood through its universal mapping property (UMP), which characterizes the limit as an object representing cones to that diagram. For example, the product of two objects \(A\) and \(B\) in a category \(\mathcal{C}\) is a limit given by an object \(P\) equipped with projections \(\pi_A: P \to A\) and \(\pi_B: P \to B\), and any other cone factors uniquely through \(P\). Similarly, the equalizer of two morphisms \(f, g: A \to B\) is a limit object \(E\) with a morphism \(e: E \to A\) satisfying \(f \circ e = g \circ e\), and it is universal among all such cones.
Universal Property: Uniqueness Up to Isomorphism
The universal property guarantees the uniqueness of limits up to a unique isomorphism, ensuring any two limit objects of the same diagram are isomorphic in a canonical way. This property provides a precise characterization that defines limits by a terminal cone, enforcing uniqueness within the categorical context. Consequently, universal properties serve as a powerful tool for identifying objects uniquely determined by their morphisms and commutative diagrams.
Constructing Limits Using Universal Property
Limits in category theory are constructed through universal properties that characterize them as cones uniquely factoring through any other cone over a diagram. This universal mapping property ensures the limit object represents a terminal object in the category of cones, establishing its uniqueness up to isomorphism. By identifying this universal factorization, one translates abstract limit constructions into explicit morphism-based definitions within categorical contexts.
Comparing Limits, Colimits, and Their Universal Properties
Limits and colimits are categorical constructs characterized by their universal properties, which define unique morphisms that factor through cones or cocones, respectively. Limits represent universal cones that factorize all other cones to a diagram, ensuring a universal solution to limiting behavior, while colimits represent universal cocones that universally factor all cocones and aggregate data. This contrast highlights limits as terminal objects in the category of cones and colimits as initial objects in the category of cocones, reflecting their fundamental duality in category theory.
Applications of Limit and UMP in Mathematics
Limits provide a unified framework to construct objects such as products, pullbacks, and inverses in categories, facilitating the solution of equations and the characterization of algebraic structures. The Universal Mapping Property (UMP) identifies and characterizes objects uniquely up to isomorphism by their universal relationships, enabling the definition of free objects, colimits, and adjoint functors. Both Limit constructions and UMP are foundational in category theory, allowing for powerful abstractions in algebraic topology, algebraic geometry, and homological algebra.
Summary: Importance of UMP in Describing Limits
The Universal Mapping Property (UMP) provides a precise and concise characterization of limits by defining them through unique morphisms that factor through a cone. This property ensures the uniqueness and existence of these morphisms, making limits canonical and fundamental in category theory for constructing and comparing objects. UMP simplifies the study of limits by translating complex diagrammatic conditions into a universal factorization criterion, essential for understanding constructions like products, pullbacks, and inverse limits.
Limit Infographic
 libterm.com
libterm.com