The Well-Ordering Theorem states that every set can be well-ordered, meaning its elements can be arranged in an order where every non-empty subset has a least element. This theorem is fundamental in set theory and has deep connections to the Axiom of Choice and ordinal numbers. Explore the rest of the article to understand how this theorem influences mathematical reasoning and your grasp of set theory concepts.
Table of Comparison
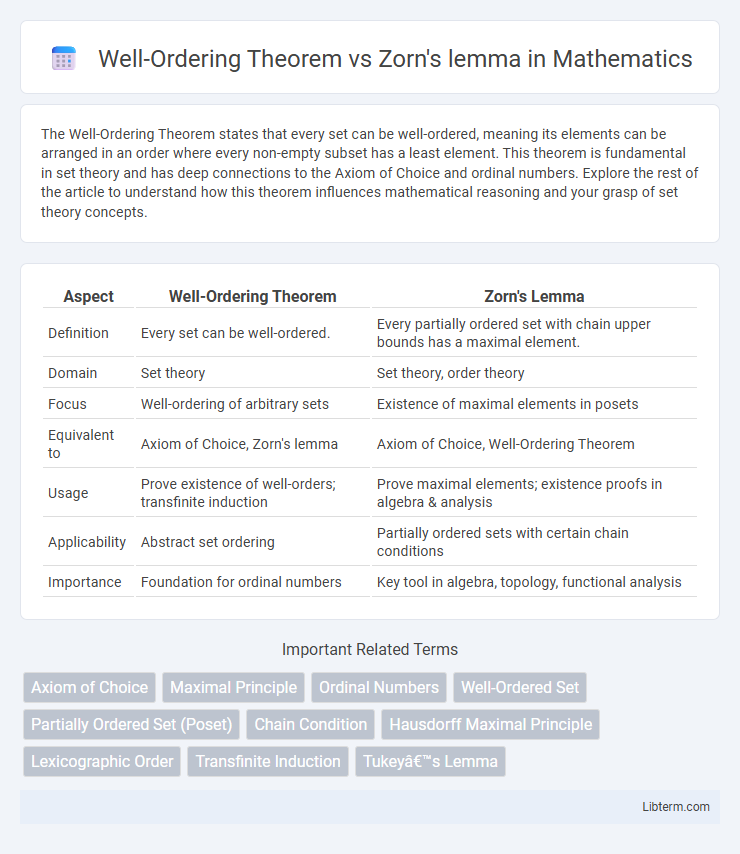
| Aspect | Well-Ordering Theorem | Zorn's Lemma |
|---|---|---|
| Definition | Every set can be well-ordered. | Every partially ordered set with chain upper bounds has a maximal element. |
| Domain | Set theory | Set theory, order theory |
| Focus | Well-ordering of arbitrary sets | Existence of maximal elements in posets |
| Equivalent to | Axiom of Choice, Zorn's lemma | Axiom of Choice, Well-Ordering Theorem |
| Usage | Prove existence of well-orders; transfinite induction | Prove maximal elements; existence proofs in algebra & analysis |
| Applicability | Abstract set ordering | Partially ordered sets with certain chain conditions |
| Importance | Foundation for ordinal numbers | Key tool in algebra, topology, functional analysis |
Introduction to Well-Ordering Theorem and Zorn’s Lemma
The Well-Ordering Theorem states that every set can be well-ordered, meaning its elements can be arranged in a sequence where every subset has a least element, a concept fundamental to set theory and ordinal numbers. Zorn's Lemma asserts that a partially ordered set in which every chain has an upper bound contains at least one maximal element, playing a crucial role in algebra and analysis. Both principles are equivalent to the Axiom of Choice, serving as foundational tools for proving existence theorems in mathematics.
Historical Background and Development
The Well-Ordering Theorem and Zorn's Lemma both emerged from the foundational work in set theory by Ernst Zermelo and later mathematicians addressing the Axiom of Choice in the early 20th century. Zermelo introduced the Well-Ordering Theorem in 1904 to demonstrate that every set can be well-ordered if the Axiom of Choice holds. Zorn's Lemma, formulated by Max Zorn in 1935, provided an alternative equivalent statement to the Axiom of Choice, facilitating proofs in algebra and analysis by leveraging partially ordered sets and maximal elements.
Formal Definitions
The Well-Ordering Theorem states that every set can be equipped with a well-ordering, meaning a total order in which every non-empty subset has a least element. Zorn's Lemma asserts that in any partially ordered set where every chain (totally ordered subset) has an upper bound, there exists at least one maximal element. Both principles are equivalent in Zermelo-Fraenkel set theory with the Axiom of Choice, serving as foundational tools in order theory and proving existence results.
Importance in Set Theory
The Well-Ordering Theorem establishes that every set can be well-ordered, providing a foundational tool for constructing ordinal numbers and proving cardinal comparability in set theory. Zorn's Lemma, equivalent to the Axiom of Choice, is pivotal for demonstrating the existence of maximal elements in partially ordered sets, thereby facilitating proofs in algebra, analysis, and topology. Both principles are central in the study of infinite sets and underpin many fundamental results in modern set theory and its applications.
Relationship to the Axiom of Choice
The Well-Ordering Theorem and Zorn's Lemma are both equivalent to the Axiom of Choice in standard set theory, meaning each can be derived from the others. The Well-Ordering Theorem asserts that every set can be well-ordered, while Zorn's Lemma guarantees the existence of maximal elements in partially ordered sets under certain conditions. Their equivalence highlights the foundational role of the Axiom of Choice in enabling these important results in mathematics.
Well-Ordering Theorem: Applications and Examples
The Well-Ordering Theorem, stating every set can be well-ordered, is fundamental in set theory and underpins proofs in cardinal arithmetic and ordinal theory. It enables the construction of transfinite induction and recursion, facilitating the definition of functions over arbitrary sets. Applications include establishing the existence of bases in vector spaces and proving equivalences in axiomatic set theory alongside Zorn's lemma.
Zorn’s Lemma: Applications and Examples
Zorn's Lemma is a fundamental tool in algebra, topology, and analysis used to prove the existence of maximal elements in partially ordered sets where every chain has an upper bound. It is instrumental in demonstrating the existence of bases in vector spaces, maximal ideals in rings, and extending linear functionals in functional analysis. The lemma's versatility lies in its applicability to structures lacking explicit maximal elements, providing an alternative to constructive proofs facilitated by the Well-Ordering Theorem.
Logical Equivalence and Proof Outlines
The Well-Ordering Theorem and Zorn's Lemma are logically equivalent statements in set theory, each implying the Axiom of Choice. The Well-Ordering Theorem asserts that every set can be well-ordered, whereas Zorn's Lemma states that a partially ordered set in which every chain has an upper bound contains at least one maximal element. Proof outlines demonstrate that using Zorn's Lemma, one constructs maximal elements to define well-orderings, and conversely, assuming the Well-Ordering Theorem enables the maximal element's existence in any partially ordered set.
Common Misconceptions and Clarifications
The Well-Ordering Theorem and Zorn's Lemma, both equivalent formulations of the Axiom of Choice, are often misconceived as independent or hierarchical principles. The Well-Ordering Theorem states every set can be well-ordered, while Zorn's Lemma asserts that a partially ordered set with every chain having an upper bound contains a maximal element; misunderstanding their equivalence leads to confusion in set theory and logic. Clarifying this equivalence is crucial for accurately applying these concepts in proofs involving order structures and maximal elements.
Conclusion: Comparing Theoretical and Practical Impact
The Well-Ordering Theorem and Zorn's Lemma both serve as crucial equivalents of the Axiom of Choice, underpinning major results in set theory and logic. While the Well-Ordering Theorem provides a theoretical foundation by asserting every set can be well-ordered, Zorn's Lemma offers a more practical tool for proving the existence of maximal elements in partially ordered sets, instrumental in algebra and functional analysis. Their equivalence confirms their foundational significance, yet Zorn's Lemma typically yields more straightforward applications in mathematical practice.
Well-Ordering Theorem Infographic
 libterm.com
libterm.com