A graded ring is an algebraic structure decomposed into a direct sum of abelian groups or modules, indexed by non-negative integers or another monoid, where the multiplication respects the grading. This concept plays a crucial role in various areas of mathematics, including algebraic geometry, homological algebra, and representation theory. Explore the rest of the article to understand how graded rings function and their applications in your mathematical studies.
Table of Comparison
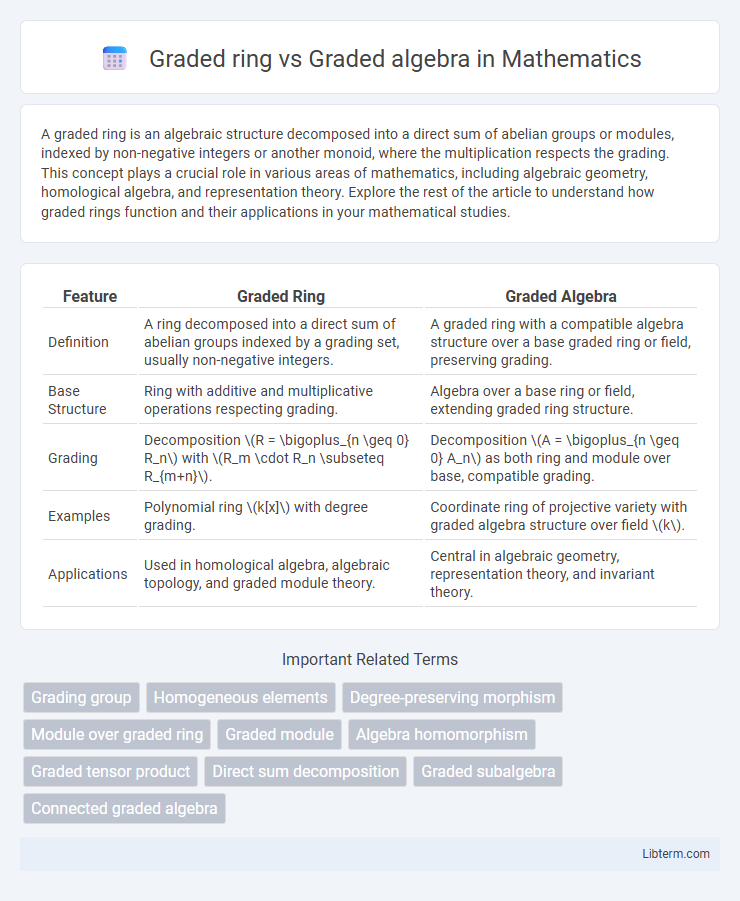
| Feature | Graded Ring | Graded Algebra |
|---|---|---|
| Definition | A ring decomposed into a direct sum of abelian groups indexed by a grading set, usually non-negative integers. | A graded ring with a compatible algebra structure over a base graded ring or field, preserving grading. |
| Base Structure | Ring with additive and multiplicative operations respecting grading. | Algebra over a base ring or field, extending graded ring structure. |
| Grading | Decomposition \(R = \bigoplus_{n \geq 0} R_n\) with \(R_m \cdot R_n \subseteq R_{m+n}\). | Decomposition \(A = \bigoplus_{n \geq 0} A_n\) as both ring and module over base, compatible grading. |
| Examples | Polynomial ring \(k[x]\) with degree grading. | Coordinate ring of projective variety with graded algebra structure over field \(k\). |
| Applications | Used in homological algebra, algebraic topology, and graded module theory. | Central in algebraic geometry, representation theory, and invariant theory. |
Introduction to Graded Structures
Graded rings are algebraic structures decomposed into direct sums of abelian groups or modules indexed by a grading set, often the integers, enabling a layer-wise study of ring elements and operations. Graded algebras extend graded rings by incorporating a compatible scalar multiplication from a base field or ring, allowing interplay between grading and algebraic structure. Understanding graded structures facilitates analyzing homological properties, module theory, and algebraic geometry through filtration and degree-based components.
Definition of Graded Rings
A graded ring is a ring decomposed into a direct sum of abelian groups \( R = \bigoplus_{n \in \mathbb{Z}} R_n \) such that the product of elements satisfies \( R_m \cdot R_n \subseteq R_{m+n} \) for all integers \( m, n \). This structure generalizes rings by incorporating a grading that respects multiplication, enabling finer algebraic and homological analysis. In contrast, a graded algebra is a graded ring equipped with a compatible scalar multiplication over a base field or ring, emphasizing its module and algebra structure simultaneously.
Definition of Graded Algebras
A graded algebra is a graded ring equipped with a compatible algebra structure over a commutative ring, such that the multiplication respects the grading by mapping the product of elements from degree \(m\) and degree \(n\) into degree \(m+n\). Specifically, a graded algebra \(A = \bigoplus_{n \geq 0} A_n\) is an algebra where each component \(A_n\) is an additive subgroup or module, and the product satisfies \(A_m \cdot A_n \subseteq A_{m+n}\). This structure generalizes graded rings by requiring an underlying ring homomorphism from a base ring, providing a richer framework for algebraic operations within the graded components.
Key Differences between Graded Rings and Graded Algebras
Graded rings are algebraic structures decomposed into a direct sum of abelian groups indexed by degrees, where multiplication respects the grading; graded algebras extend graded rings by incorporating a compatible scalar multiplication from a base field or ring, thus forming vector spaces with graded components. The key difference lies in graded algebras possessing a module structure over a base ring or field in addition to the graded ring properties, enabling richer operations such as scalar multiplication on each graded piece. Graded rings focus solely on internal multiplication across graded components, while graded algebras emphasize both the graded ring structure and the algebraic action of scalars from an external field or ring.
Examples of Graded Rings
Examples of graded rings include polynomial rings \( k[x] \) with the degree grading where each monomial \( x^n \) lies in degree \( n \), and group rings \( k[G] \) graded by the group \( G \). Another instance is the ring of formal power series \( k[[x]] \) equipped with the filtration-induced grading by powers of \( x \). These graded rings serve as foundational structures, while graded algebras often impose additional module or algebraic compatibility conditions over a base field or ring.
Examples of Graded Algebras
Graded algebras are algebraic structures equipped with a decomposition into direct sums of subspaces, where the product of elements respects the grading, such as the polynomial ring \( k[x] \) graded by degree or the exterior algebra generated by vector spaces. Graded rings, in contrast, are simply rings with a similar direct sum decomposition but without requiring an algebra structure over a field. Examples of graded algebras include the symmetric algebra of a vector space, the group algebra of a graded group, and the cohomology ring of a topological space, which carries a natural grading by degree.
Structural Properties and Homomorphisms
A graded ring is a ring decomposed into a direct sum of abelian groups indexed by a grading set, typically the non-negative integers, where the product of elements respects the grading structure. A graded algebra extends the concept of a graded ring by incorporating a compatible module structure over a base ring or field, preserving both the grading and scalar multiplication. Homomorphisms between graded rings or graded algebras maintain the grading by mapping elements of a given degree to elements of the same degree, thereby ensuring the preservation of the graded structure and the algebraic operations.
Applications in Mathematics and Physics
Graded rings structure algebraic entities by decomposing them into direct sums indexed by an abelian group, enabling refined analysis of ring homomorphisms and module theory in algebraic geometry and homological algebra. Graded algebras extend graded rings by incorporating compatible multiplication with scalar fields, crucial in constructing cohomology rings and Lie algebra representations that model symmetry and conservation laws in theoretical physics. Both frameworks underpin advancements in quantum field theory and string theory, where grading reflects particle states or energy levels, facilitating computations in gauge theories and deformation quantization.
Graded Modules over Graded Rings and Algebras
Graded modules over graded rings provide a structured way to study modules decomposed into direct sums indexed by degrees, with module operations respecting grading. In contrast, graded algebras extend graded rings by incorporating compatible algebraic structures, allowing richer interactions between graded components through multiplication. Understanding graded modules over graded algebras is essential for exploring homological properties and morphisms that preserve both grading and algebraic operations.
Summary and Comparative Table
A graded ring is an algebraic structure decomposed into a direct sum of abelian groups indexed by degrees, where the product of elements respects the grading, while a graded algebra extends this concept by incorporating a ring action from a base ring or field, making it both a graded ring and a module. In a comparative summary, graded rings emphasize internal graded multiplicative structures, whereas graded algebras highlight compatibility with scalars from an external ring. The table below outlines key differences: | Feature | Graded Ring | Graded Algebra | |-------------------------|--------------------------------------|--------------------------------------| | Structure | Direct sum of abelian groups | Graded ring + module over base ring | | Multiplicative action | Internal, respects grading | Internal graded multiplication + scalar multiplication | | Base field or ring | Not required explicitly | Requires base ring or field | | Examples | Polynomial rings graded by degree | Polynomial algebras, tensor algebras | | Applications | Homological algebra, algebraic topology| Representation theory, deformation theory |
Graded ring Infographic
 libterm.com
libterm.com