The cross product is a vector operation in three-dimensional space that produces a vector perpendicular to the plane formed by two input vectors. Its magnitude equals the area of the parallelogram spanned by the original vectors, making it essential for calculations involving torque, rotational motion, and physics applications. Explore the rest of the article to deepen your understanding of cross product properties and practical uses.
Table of Comparison
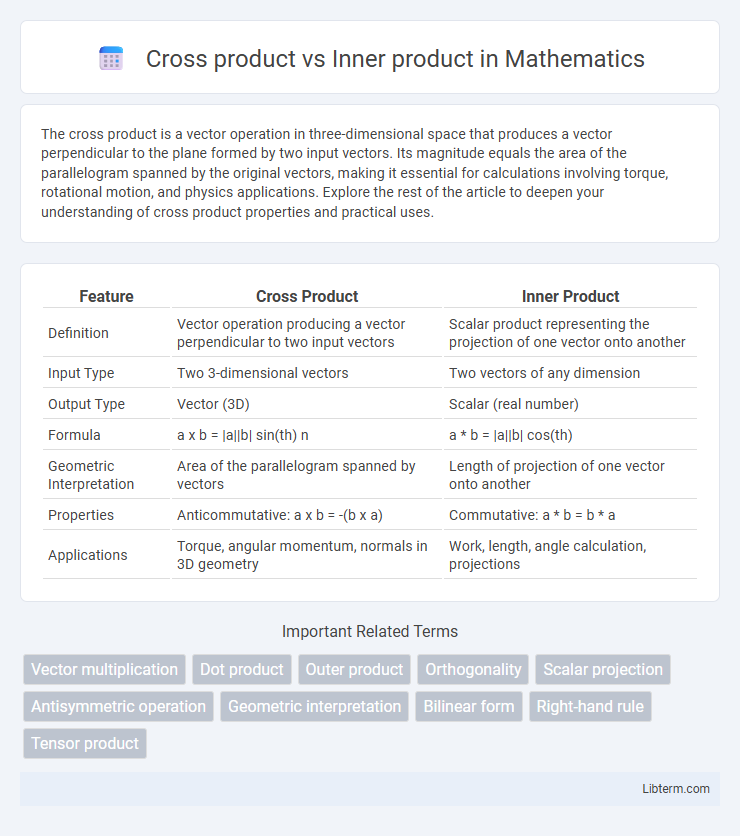
| Feature | Cross Product | Inner Product |
|---|---|---|
| Definition | Vector operation producing a vector perpendicular to two input vectors | Scalar product representing the projection of one vector onto another |
| Input Type | Two 3-dimensional vectors | Two vectors of any dimension |
| Output Type | Vector (3D) | Scalar (real number) |
| Formula | a x b = |a||b| sin(th) n | a * b = |a||b| cos(th) |
| Geometric Interpretation | Area of the parallelogram spanned by vectors | Length of projection of one vector onto another |
| Properties | Anticommutative: a x b = -(b x a) | Commutative: a * b = b * a |
| Applications | Torque, angular momentum, normals in 3D geometry | Work, length, angle calculation, projections |
Introduction to Cross Product and Inner Product
The cross product in vector algebra produces a vector perpendicular to two input vectors in three-dimensional space, embodying both magnitude and direction. The inner product, or dot product, calculates a scalar representing the magnitude of one vector projected onto another, reflecting their directional alignment. Understanding these products is essential for applications in physics, engineering, and computer graphics where vector operations determine spatial relationships.
Fundamental Definitions
The cross product is a binary operation on two vectors in three-dimensional space resulting in a vector orthogonal to both original vectors, defined by the determinant of a matrix formed by unit vectors and vector components. The inner product, also known as the dot product, produces a scalar by multiplying corresponding vector components and summing the results, measuring the magnitude of projection of one vector onto another. While the cross product emphasizes vector orthogonality and area computation, the inner product focuses on angle calculation and vector similarity.
Key Differences at a Glance
The cross product produces a vector perpendicular to the plane formed by two input vectors, with magnitude equal to the area of the parallelogram they span, while the inner product yields a scalar representing the cosine of the angle between the vectors multiplied by their magnitudes. The cross product is defined only in three-dimensional space, whereas the inner product generalizes to any dimension and forms the basis for concepts like vector length and orthogonality. The inner product is commutative, meaning the order of vectors does not affect the result, but the cross product is anti-commutative, changing sign when the order of vectors is swapped.
Mathematical Representation
The cross product is a binary operation on two vectors in three-dimensional space resulting in a third vector perpendicular to both, mathematically represented as A x B = |A||B|sin(th)n, where th is the angle between vectors and n is the unit vector perpendicular to the plane containing A and B. The inner product, or dot product, is a scalar defined as A * B = |A||B|cos(th), quantifying the projection of one vector onto another. Both products depend on vector magnitudes and the angle th, but the cross product yields a vector orthogonal to the operands, while the inner product produces a scalar value.
Geometric Interpretation
The cross product produces a vector perpendicular to the plane defined by two input vectors, representing the area of the parallelogram they form, with direction given by the right-hand rule. The inner product, or dot product, calculates a scalar representing the magnitude of one vector projected onto another, corresponding to the cosine of the angle between them. Geometrically, the cross product encodes orientation and area, while the inner product encodes similarity and angle.
Applications in Physics and Engineering
The cross product is essential in physics and engineering for calculating torque, angular momentum, and magnetic force, as it produces a vector perpendicular to two given vectors, representing rotational effects and directions. Inner products are crucial for determining work done by a force, projections, and signal correlations by providing scalar values that measure vector magnitudes and directional alignment. Both products enable precise modeling and analysis in mechanics, electromagnetism, and structural engineering, supporting design and optimization.
Properties and Rules
The cross product produces a vector perpendicular to two input vectors, with magnitude equal to the area of the parallelogram they span, following the right-hand rule and anti-commutative property (A x B = -B x A). The inner product (dot product) yields a scalar representing the cosine similarity of two vectors, is commutative (A * B = B * A), distributive over addition, and linear in each argument. Cross product is defined only in three-dimensional space, whereas the inner product generalizes to any dimension with properties like positivity and bilinearity.
Computational Methods
The cross product computes a vector orthogonal to two given vectors using a determinant-based formula suited for three-dimensional space, often implemented through direct coordinate calculations or skew-symmetric matrices. The inner product, or dot product, calculates a scalar representing the cosine of the angle between vectors, typically computed via element-wise multiplication followed by summation, enabling projection and similarity metrics. Efficient computational methods exploit vectorization and hardware acceleration, with cross products relying on fewer arithmetic operations in fixed dimensions and inner products benefiting from optimized linear algebra libraries for high-dimensional data.
Common Mistakes and Misconceptions
Many confuse the cross product and inner product by assuming both produce scalar results, while the cross product actually yields a vector orthogonal to the original vectors. A common mistake is applying the inner product's commutative property to the cross product, which is anti-commutative, meaning \( \mathbf{a} \times \mathbf{b} = -(\mathbf{b} \times \mathbf{a}) \). Misunderstandings also arise in geometric interpretation: the inner product measures the cosine of the angle between vectors, representing projection, whereas the cross product calculates the area of the parallelogram spanned by the vectors.
Summary and Final Comparison
The cross product generates a vector perpendicular to two input vectors in three-dimensional space, with magnitude representing the area of the parallelogram they span, while the inner product (dot product) produces a scalar measuring the cosine of the angle between vectors, indicating their directional similarity. Cross product is exclusive to three dimensions and is useful for torque and rotational dynamics, whereas the inner product applies in any dimension for projections and angle computations. Final comparison highlights that the cross product emphasizes vector orthogonality and spatial orientation, while the inner product focuses on scalar magnitude and cosine-based angular relationships.
Cross product Infographic
 libterm.com
libterm.com