Bounded refers to limits or restrictions within which something operates or exists, defining clear parameters that prevent exceeding or expanding beyond set boundaries. This concept applies in various fields such as mathematics, computer science, and psychology, where understanding constraints helps optimize performance and ensure predictable outcomes. Explore the rest of the article to discover how bounded principles influence your everyday decisions and problem-solving strategies.
Table of Comparison
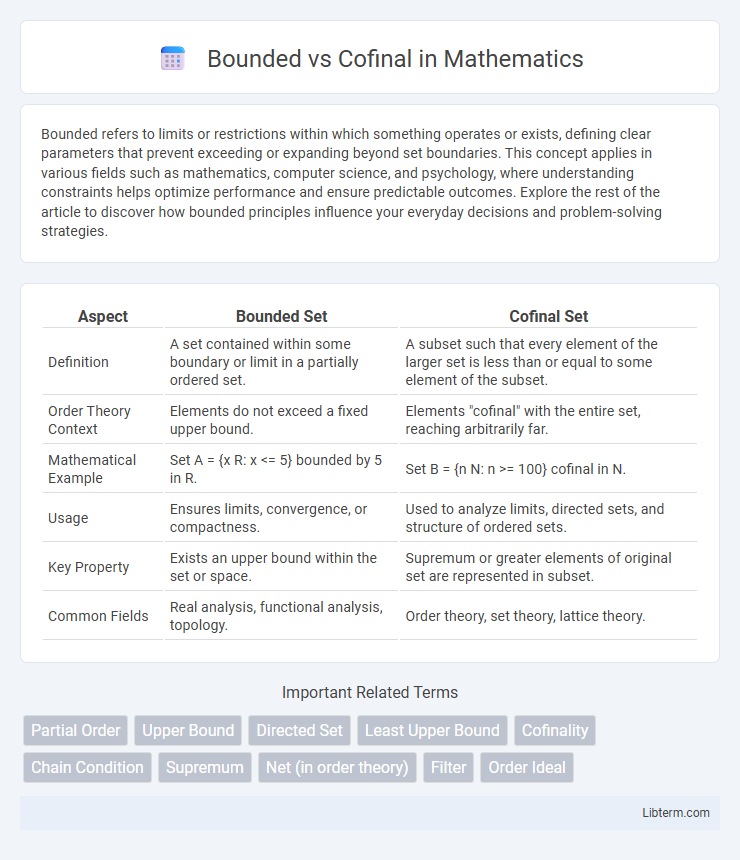
| Aspect | Bounded Set | Cofinal Set |
|---|---|---|
| Definition | A set contained within some boundary or limit in a partially ordered set. | A subset such that every element of the larger set is less than or equal to some element of the subset. |
| Order Theory Context | Elements do not exceed a fixed upper bound. | Elements "cofinal" with the entire set, reaching arbitrarily far. |
| Mathematical Example | Set A = {x R: x <= 5} bounded by 5 in R. | Set B = {n N: n >= 100} cofinal in N. |
| Usage | Ensures limits, convergence, or compactness. | Used to analyze limits, directed sets, and structure of ordered sets. |
| Key Property | Exists an upper bound within the set or space. | Supremum or greater elements of original set are represented in subset. |
| Common Fields | Real analysis, functional analysis, topology. | Order theory, set theory, lattice theory. |
Introduction to Bounded and Cofinal Concepts
Bounded and cofinal concepts are fundamental in order theory, describing relationships within partially ordered sets. A subset is bounded if there exists an upper or lower bound within the set, limiting the extent of its elements. In contrast, a cofinal subset intersects every upper segment of the poset, ensuring it reaches arbitrarily high elements relative to the order.
Defining Bounded Sets
Bounded sets in mathematics are collections of elements contained within specific limits, ensuring every member lies between two fixed points in an ordered set. Defining bounded sets requires identifying an upper bound and a lower bound that encapsulate all elements, guaranteeing no values fall outside this range. This concept contrasts with cofinal sets, where elements approach or surpass bounds without restriction, emphasizing containment and limitation in bounded sets.
Defining Cofinal Sets
Cofinal sets in order theory are subsets of a partially ordered set where every element of the original set is less than or equal to some element in the cofinal subset, ensuring the set is unbounded above. These sets contrast with bounded subsets, which are contained within some upper bound in the ordering. Defining cofinal sets is essential in understanding concepts like directed sets, filters, and limits in topology and algebra.
Key Differences Between Bounded and Cofinal
Bounded sets in order theory are subsets of a partially ordered set where all elements lie below some fixed upper bound, emphasizing containment within limits. Cofinal sets, by contrast, contain elements that reach arbitrarily high in the order, ensuring every element of the entire set is less than or equal to some element in the cofinal subset. The key difference lies in boundedness restricting elements under a specific limit, while cofinality guarantees coverage beyond all lower elements, highlighting opposite aspects of order structure.
Importance in Order Theory
Bounded and cofinal subsets play crucial roles in order theory by characterizing the structure of partially ordered sets (posets). Bounded subsets have upper or lower bounds that define limits within the poset, affecting completeness properties and the existence of suprema or infima. Cofinal subsets intersect every upper segment, ensuring the representation of "large" elements and influencing directedness and the ability to approximate elements from above.
Applications in Mathematics
Bounded sets in mathematics are crucial for defining limits and continuity, often applied in real analysis and topology to establish convergence criteria and compactness. Cofinal subsets play a significant role in order theory and set theory, aiding in the characterization of directed sets and in ordinal analysis used within transfinite induction and recursion. Both concepts underpin the structure of posets and lattices, essential in fields such as algebra, logic, and theoretical computer science for model construction and complexity classification.
Boundedness in Real Numbers
Boundedness in real numbers refers to a set having both an upper and a lower limit within the real number line, ensuring all elements lie within a finite interval. A bounded set, such as [a, b], where a and b are real numbers with a <= b, contrasts with an unbounded set that extends infinitely in at least one direction. This property is critical in analysis for defining limits, continuity, and compactness in real-valued functions and sequences.
Cofinality in Ordinal and Cardinal Numbers
Cofinality in ordinal numbers refers to the smallest ordinal type of an unbounded subset within a given ordinal, capturing how the ordinal can be approached by smaller elements. For cardinal numbers, cofinality measures the minimum cardinality of a set of smaller cardinals whose supremum equals the given cardinal, directly impacting the structure of infinite cardinals. Understanding cofinality distinguishes regular cardinals, whose cofinality equals the cardinal itself, from singular cardinals characterized by smaller cofinality values.
Real-World Examples of Bounded and Cofinal
Bounded sets are commonly seen in real-world contexts such as temperature ranges within a controlled environment, where values cannot exceed physical limits. Cofinal sets appear in project management timelines when milestones continually extend towards a deadline without an upper bound until completion. These examples illustrate how bounded and cofinal concepts apply to practical constraints and continuous progress scenarios.
Summary and Comparative Insights
Bounded sets contain elements limited by some upper or lower boundary, ensuring no elements exceed certain values, whereas cofinal sets have members that eventually surpass every element of the original set, extending infinitely. In order theory, boundedness defines constraints, while cofinality measures the ability of a subset to approximate or reach beyond the entire set's supremum. Comparing both highlights how boundedness restricts range within limits, and cofinality emphasizes unbounded growth or extension within ordered structures.
Bounded Infographic
 libterm.com
libterm.com