K-theory groups classify vector bundles over a space, capturing their algebraic and topological properties in a structured manner that helps analyze complex geometric spaces. These groups play a crucial role in various mathematical fields, including topology, algebraic geometry, and operator algebras, by providing invariants that detect subtle differences between spaces. Explore the rest of the article to deepen Your understanding of how K-theory groups illuminate the rich interplay between algebra and topology.
Table of Comparison
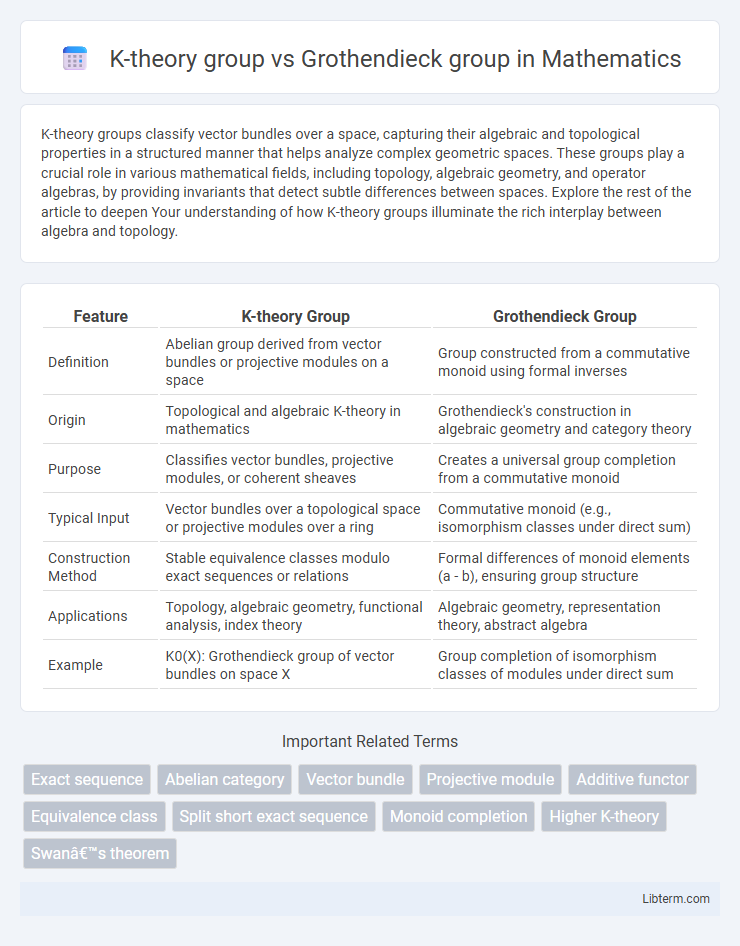
| Feature | K-theory Group | Grothendieck Group |
|---|---|---|
| Definition | Abelian group derived from vector bundles or projective modules on a space | Group constructed from a commutative monoid using formal inverses |
| Origin | Topological and algebraic K-theory in mathematics | Grothendieck's construction in algebraic geometry and category theory |
| Purpose | Classifies vector bundles, projective modules, or coherent sheaves | Creates a universal group completion from a commutative monoid |
| Typical Input | Vector bundles over a topological space or projective modules over a ring | Commutative monoid (e.g., isomorphism classes under direct sum) |
| Construction Method | Stable equivalence classes modulo exact sequences or relations | Formal differences of monoid elements (a - b), ensuring group structure |
| Applications | Topology, algebraic geometry, functional analysis, index theory | Algebraic geometry, representation theory, abstract algebra |
| Example | K0(X): Grothendieck group of vector bundles on space X | Group completion of isomorphism classes of modules under direct sum |
Introduction to K-Theory and Grothendieck Group
K-theory group formalizes vector bundles over a topological space, capturing their stable isomorphism classes via algebraic invariants, essential in fields such as algebraic geometry and topology. The Grothendieck group emerges from a commutative monoid by formally introducing inverses, enabling the transition from semi-group structures of objects like vector bundles or coherent sheaves to an abelian group framework. Both concepts underpin the classification of objects up to stable equivalence, with K-theory groups often constructed as specific Grothendieck groups associated with categories of vector bundles or modules.
Historical Background and Motivation
The Grothendieck group emerged in the 1950s as a construction to universally relate abelian monoids to abelian groups, providing a foundational tool in algebraic geometry and number theory. K-theory groups, introduced by Alexander Grothendieck and Michael Atiyah, extended this construction to classify vector bundles and projective modules, offering deep insights into topology and algebra. The motivation behind K-theory was to generalize the Grothendieck group concept to capture richer algebraic and geometric structures, enabling the development of higher algebraic K-theory and applications in index theory.
Fundamental Definitions
The K-theory group, denoted K(X), arises from vector bundles over a topological space or projective modules over a ring, capturing isomorphism classes with operations reflecting direct sum and tensor product structures. The Grothendieck group, constructed from a commutative monoid, formalizes the process of group completion by adding inverses, serving as an abstract foundation for K-theory groups. Both groups share the universal property of mapping monoids to abelian groups, but K-theory incorporates additional geometric or algebraic structure specific to bundles or modules.
Construction of the Grothendieck Group
The Grothendieck group is constructed from a commutative monoid by formally adding inverses to each element, transforming the monoid into an abelian group. In comparison, the K-theory group, particularly the K_0 group, is defined via the Grothendieck group construction applied to the monoid of isomorphism classes of vector bundles or projective modules under direct sum. This process captures the essential algebraic structure, enabling classification and analysis of objects such as vector bundles through stable equivalence in algebraic and topological K-theory.
K-Theory Group: Concepts and Examples
K-theory groups classify vector bundles over a topological space, providing a powerful tool in topology and algebraic geometry by encoding information about projective modules and their isomorphism classes. The construction involves forming the Grothendieck group from the monoid of isomorphism classes of vector bundles under the direct sum operation, yielding an abelian group that captures stable equivalence classes. Classic examples include the K_0 group, which relates to vector bundles over compact Hausdorff spaces, and K_1, which connects to invertible matrices and automorphisms, highlighting their role in both algebraic and topological contexts.
Relationship Between K-Theory and Grothendieck Group
The Grothendieck group serves as the foundational construction for K-theory by formalizing the notion of group completion of a commutative monoid arising from isomorphism classes of vector bundles or modules. K-theory groups extend the Grothendieck group's principles to incorporate additional structures such as exact sequences and homotopy-theoretic data, enabling the classification of vector bundles on topological spaces or projective modules over rings. The relationship between them is intrinsic: K-theory generalizes the Grothendieck group framework to encode richer algebraic and topological information beyond the purely additive context.
Key Differences and Similarities
The K-theory group and the Grothendieck group both arise from constructions aiming to classify vector bundles or modules over a ring, capturing their isomorphism classes with an added group structure. The Grothendieck group is a general abstraction that takes a commutative monoid and formally adds inverses to obtain an abelian group, often applied to categories like finitely generated projective modules, while K-theory groups specifically extend this concept to higher algebraic and topological contexts, encoding complex structural information such as exact sequences or homotopy invariants. Both share the foundational idea of group completion and functorial behavior, yet K-theory groups rely on additional sophisticated machinery from homotopy theory and stable homotopy categories, enabling richer invariants for classification beyond the basic additive relations used in Grothendieck groups.
Applications in Algebra and Topology
K-theory groups provide a powerful framework for classifying vector bundles over topological spaces, enabling deep connections between algebraic and topological invariants. Grothendieck groups, constructed from exact categories or monoids, serve as algebraic tools to capture equivalence classes of objects, such as modules or coherent sheaves, facilitating computations in algebraic K-theory. Applications in algebra include classification of projective modules and understanding ring structures, while in topology, these groups aid in index theory, characteristic classes, and the study of stable homotopy types.
Notable Theorems and Results
The K-theory group and the Grothendieck group both arise from the formal group completion of isomorphism classes of objects in a suitable category, but K-theory extends beyond algebraic vector bundles to include higher algebraic and topological invariants. Notable theorems include the Atiyah-Hirzebruch spectral sequence, connecting topological K-theory to singular cohomology, and Quillen's theorem establishing the equivalence between higher algebraic K-theory and homotopy groups of certain classifying spaces. The Grothendieck group captures fundamental additivity properties and serves as the foundation for defining characteristic classes, such as the Chern character, which link algebraic and differential geometric invariants.
Conclusion and Further Reading
K-theory groups generalize vector bundle classification by incorporating homotopy-theoretic methods, while Grothendieck groups provide an algebraic framework capturing isomorphism classes of objects in an exact category through formal differences. The K-theory group often extends Grothendieck group concepts, adding higher algebraic and topological information relevant in advanced geometry and topology. For further reading, foundational texts include Atiyah's "K-Theory" and Weibel's "The K-Book," which detail algebraic and topological K-theory and their connections to Grothendieck groups.
K-theory group Infographic
 libterm.com
libterm.com