Group dynamics significantly influence team productivity and individual motivation within any organization. Understanding how different personalities and communication styles interact can enhance collaboration and conflict resolution. Discover effective strategies to optimize your group performance by reading the full article.
Table of Comparison
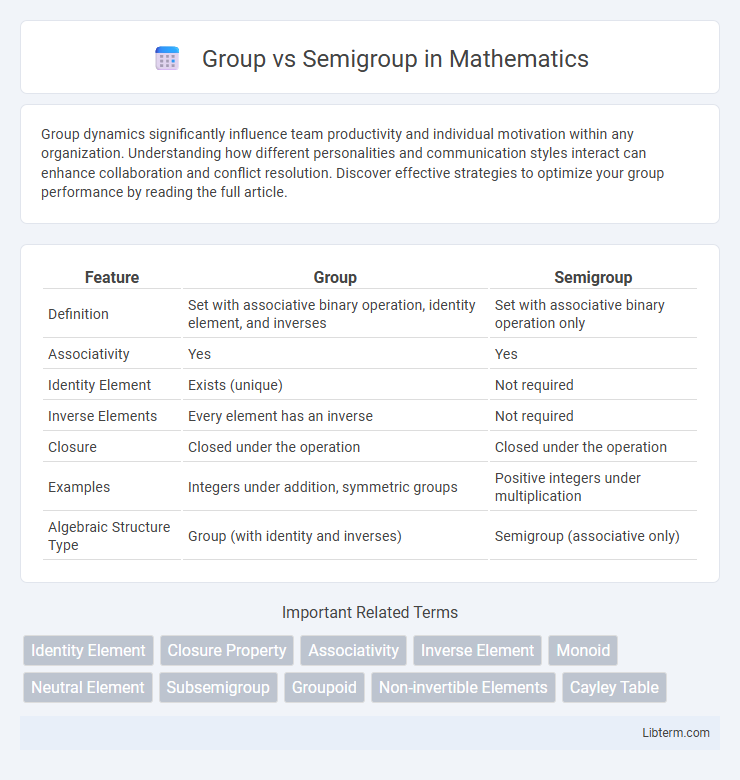
| Feature | Group | Semigroup |
|---|---|---|
| Definition | Set with associative binary operation, identity element, and inverses | Set with associative binary operation only |
| Associativity | Yes | Yes |
| Identity Element | Exists (unique) | Not required |
| Inverse Elements | Every element has an inverse | Not required |
| Closure | Closed under the operation | Closed under the operation |
| Examples | Integers under addition, symmetric groups | Positive integers under multiplication |
| Algebraic Structure Type | Group (with identity and inverses) | Semigroup (associative only) |
Introduction to Groups and Semigroups
Groups are algebraic structures consisting of a set combined with an associative binary operation, an identity element, and inverses for every element, ensuring closure and invertibility. Semigroups are more general structures where only closure and associativity of the binary operation are required, lacking necessarily an identity or inverses. The distinction highlights that every group is a semigroup, but not every semigroup qualifies as a group due to the absence of identity and inverses.
Defining a Group: Key Properties
A group is an algebraic structure consisting of a set equipped with a binary operation that satisfies four key properties: closure, associativity, the existence of an identity element, and the existence of inverses for every element. Unlike semigroups, groups guarantee both an identity element and inverses, making every element reversible under the operation. This distinction is crucial in abstract algebra, as groups enable the systematic study of symmetries and transformations through their well-defined algebraic framework.
What is a Semigroup? Core Characteristics
A semigroup is an algebraic structure consisting of a non-empty set equipped with an associative binary operation, meaning the operation satisfies the law (a * b) * c = a * (b * c) for all elements a, b, and c in the set. Unlike a group, a semigroup does not require an identity element or inverses for each element. Core characteristics of a semigroup include closure under the binary operation and the associativity property, which enable repeated application of the operation without ambiguity.
Fundamental Differences Between Groups and Semigroups
Groups possess an identity element and inverses for every element, ensuring structure closure under the operation, while semigroups require only associativity without the need for an identity or inverses. This fundamental lack of an identity element in semigroups prevents them from guaranteeing elements that "undo" the operation, a feature essential in groups. As a result, groups form a more restrictive algebraic structure that supports more robust mathematical properties than semigroups.
Common Examples of Groups in Mathematics
Groups in mathematics include familiar structures such as the set of integers under addition, showcasing closure, associativity, identity, and inverses. Another prominent example is the group of non-zero real numbers under multiplication, emphasizing invertible elements. Symmetry groups, like the permutation group on a finite set, illustrate groups in geometric and algebraic contexts through bijective transformations preserving structure.
Practical Examples of Semigroups
Semigroups are algebraic structures consisting of a set equipped with an associative binary operation, lacking the necessity for an identity element or inverses, unlike groups. In practical applications, semigroups appear in computer science through string concatenation, where combining strings forms a semigroup under concatenation without requiring an empty string or inverses. Other examples include the set of natural numbers under addition, which forms a semigroup but not a group, highlighting their relevance in contexts where closure and associativity hold without full group properties.
The Role of Identity Elements
In algebraic structures, a group requires an identity element that acts as a neutral element for all operations, meaning every element combined with the identity leaves the element unchanged. Semigroups lack an identity element, consisting only of an associative binary operation, making them less restrictive than groups. The presence of an identity element in groups ensures invertibility of each element, a key factor distinguishing groups from semigroups in abstract algebra.
Inverses in Groups vs Semigroups
Groups guarantee the existence of inverses for every element, ensuring that each element has a unique inverse such that their product is the identity element. Semigroups do not require inverses, meaning elements may lack any form of inverse, resulting in less algebraic structure and fewer symmetries. The presence of inverses in groups enables solving equations and constructing isomorphisms, which is generally impossible in semigroups without additional constraints.
Applications of Groups and Semigroups
Groups play a crucial role in cryptography, coding theory, and physics due to their well-defined algebraic structure, enabling symmetry analysis and secure communication. Semigroups find applications in automata theory, formal languages, and computer science for modeling state transitions and processing sequences without requiring invertibility. The distinction allows groups to address reversible processes, while semigroups effectively represent irreversible computations and dynamic system behaviors.
Summary: Choosing Between Groups and Semigroups
Groups feature an associative binary operation, an identity element, and inverses for every element, enabling comprehensive algebraic manipulations. Semigroups require only an associative binary operation, making them simpler but less structured for complex transformations. Selecting between groups and semigroups depends on the need for element invertibility and identity presence in the algebraic system under consideration.
Group Infographic
 libterm.com
libterm.com