A monad is a powerful abstraction in functional programming that allows you to handle side effects, data transformations, and computations in a consistent and composable way. By encapsulating values along with a context, monads provide a framework for chaining operations while maintaining code clarity and reliability. Dive into the rest of the article to discover how monads can enhance your programming skills and simplify complex tasks.
Table of Comparison
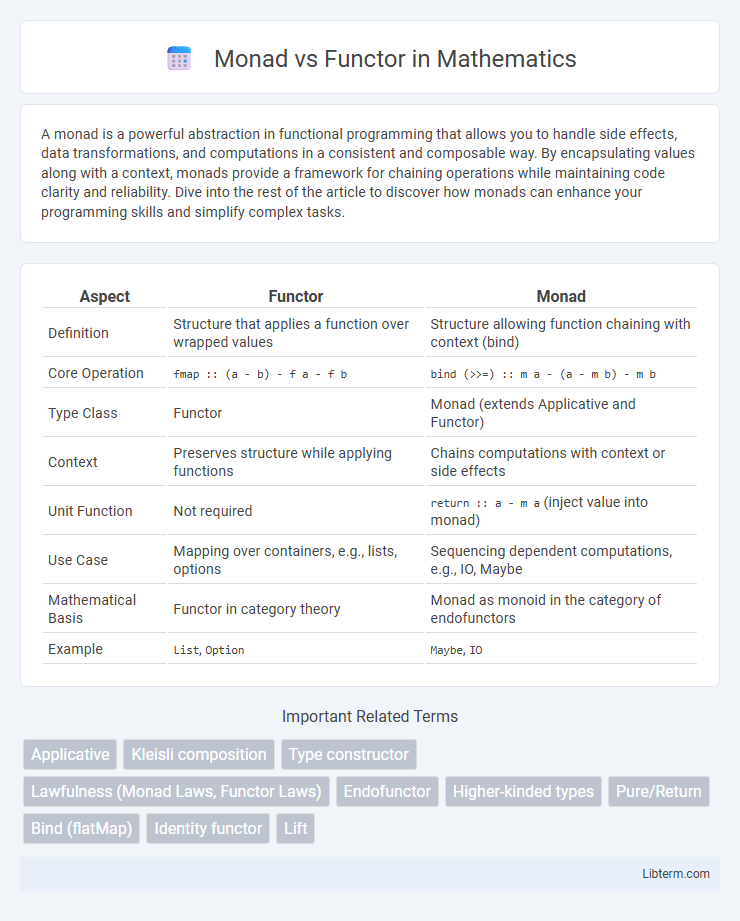
| Aspect | Functor | Monad |
|---|---|---|
| Definition | Structure that applies a function over wrapped values | Structure allowing function chaining with context (bind) |
| Core Operation | fmap :: (a - b) - f a - f b |
bind (>>=) :: m a - (a - m b) - m b |
| Type Class | Functor | Monad (extends Applicative and Functor) |
| Context | Preserves structure while applying functions | Chains computations with context or side effects |
| Unit Function | Not required | return :: a - m a (inject value into monad) |
| Use Case | Mapping over containers, e.g., lists, options | Sequencing dependent computations, e.g., IO, Maybe |
| Mathematical Basis | Functor in category theory | Monad as monoid in the category of endofunctors |
| Example | List, Option |
Maybe, IO |
Understanding Functors: The Basics
Functors are a fundamental concept in functional programming that allow mapping a function over wrapped values without altering the underlying structure. They follow the Functor laws, such as identity and composition, ensuring predictable behavior in data transformations. Understanding functors provides a basis for grasping more complex abstractions like monads, which build upon functor principles to handle computations involving context or side effects.
What is a Monad? Core Concepts
A Monad is a design pattern used in functional programming to handle side effects and manage computations in a sequential manner. It consists of three core components: a type constructor that defines how to wrap a value into the monadic context, a `bind` function (often called `flatMap` or `>>=`) that chains computations while preserving the monadic structure, and a `return` (or `pure`) function that injects a value into the monad. Unlike Functors, which only support applying a function over wrapped values, Monads enable the composition of multiple dependent operations, making them essential for complex effect management and control flow.
Key Differences Between Functors and Monads
Functors provide a mechanism to apply a function over wrapped values using the `map` operation, preserving the context without flattening nested structures. Monads extend this capability by offering the `flatMap` (or `bind`) operation, which allows chaining of computations that produce wrapped values, effectively flattening nested monadic structures. Key differences include functors supporting only context-preserving transformations, whereas monads enable sequencing of dependent operations through context flattening and chaining.
Functor Laws Explained
Functor laws consist of two main principles: identity and composition, ensuring consistent behavior when mapping functions over functorial values. The identity law states that mapping the identity function over a functor should return the functor unchanged, expressed as fmap id = id. The composition law requires that mapping the composition of two functions is equivalent to mapping one function and then mapping the other, formulated as fmap (f . g) = fmap f . fmap g, which guarantees functors preserve function composition semantics.
Monad Laws Demystified
Monad laws consist of three key principles: left identity, right identity, and associativity, which ensure consistent behavior when composing monadic operations. Left identity states that wrapping a value in a monad and then applying a function with flatMap must be the same as applying the function directly. Right identity requires that flatMapping a monadic value with the unit (or return) function leaves the monad unchanged, while associativity guarantees that the order of nested flatMap calls can be rearranged without altering the final result.
Practical Examples: Functor in Action
Functors allow you to apply a function over wrapped values in a container, such as mapping a transformation over a list or an option type without altering the structure. For example, using a functor with a list, applying a function like increment to each element results in a new list with incremented values, showcasing the preservation of context with pure functions. This contrasts with monads, which enable sequencing of operations that may also produce wrapped results, essential for handling side effects or chaining computations.
Practical Examples: Monad in Real Code
Monads, exemplified by the Maybe monad in Haskell, handle computations with context such as possible failure, enabling clean error propagation without explicit checks. For instance, chaining operations like database lookups or user input validation uses the bind operation (>>=) to seamlessly pass results while managing nullability or errors. Functors, by contrast, provide a simpler capability to apply functions over wrapped values using fmap but lack the compositional power for dependent computations that monads offer.
When to Use Functor vs Monad
Use Functor when you need to apply a function to values wrapped in a context, such as transforming data without altering the structure or introducing side effects. Monad is preferred when sequential operations depend on previous results, enabling flat mapping and handling of computations that include chaining and context-sensitive effects. Functors provide a simpler abstraction for mapping, while Monads handle more complex workflows requiring context management and side-effect control.
Advantages and Limitations of Each Abstraction
Monads provide a powerful framework for handling side effects and sequencing computations, enabling more expressive and maintainable code when dealing with complex data transformations or asynchronous operations. Functors, on the other hand, offer a simpler abstraction for mapping functions over wrapped values without changing the structure, making them ideal for less complex transformations. While monads offer greater control and flexibility, they require more cognitive overhead and can introduce complexity, whereas functors provide straightforward composability but lack the ability to chain dependent computations effectively.
Common Misconceptions About Functors and Monads
Functors are often misunderstood as simply containers with a map function, ignoring their role in preserving structure while applying functions. Monads are frequently mistaken for just functors with additional capabilities, but they provide a powerful mechanism for chaining operations with context, such as handling side effects or asynchronous computation. A common misconception is that all monads must implement certain behaviors in the same way, whereas monads vary widely in how they manage effects and sequencing.
Monad Infographic
 libterm.com
libterm.com