A fixed base point serves as a crucial reference in surveying and mapping, ensuring precise measurements and accurate spatial data alignment. It acts as an anchor from which all other positions are determined, minimizing errors and enhancing project reliability. Discover how leveraging a fixed base point can improve your surveying accuracy throughout the rest of the article.
Table of Comparison
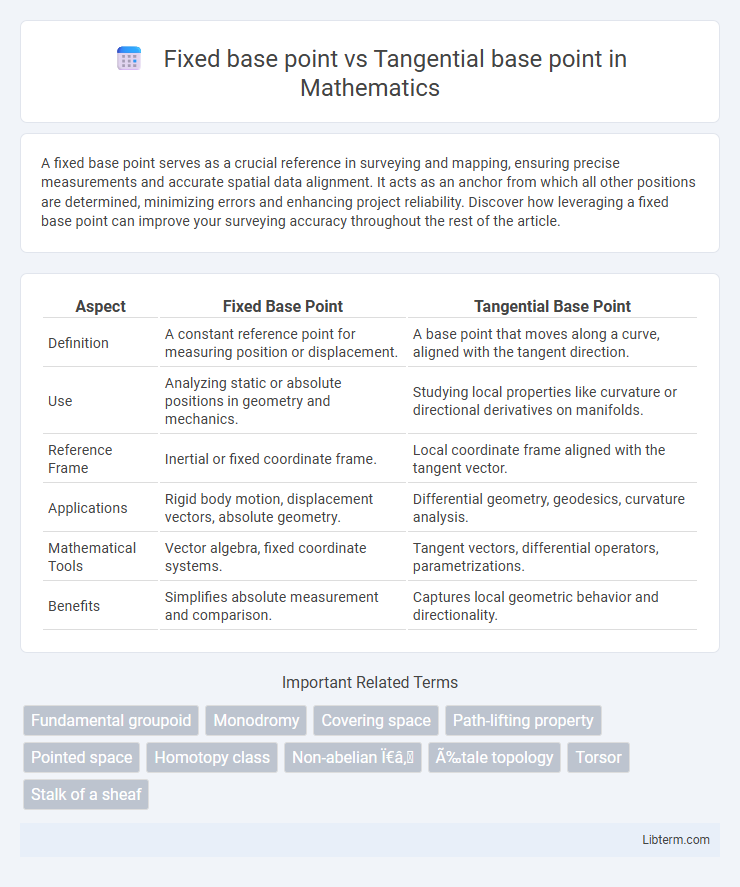
| Aspect | Fixed Base Point | Tangential Base Point |
|---|---|---|
| Definition | A constant reference point for measuring position or displacement. | A base point that moves along a curve, aligned with the tangent direction. |
| Use | Analyzing static or absolute positions in geometry and mechanics. | Studying local properties like curvature or directional derivatives on manifolds. |
| Reference Frame | Inertial or fixed coordinate frame. | Local coordinate frame aligned with the tangent vector. |
| Applications | Rigid body motion, displacement vectors, absolute geometry. | Differential geometry, geodesics, curvature analysis. |
| Mathematical Tools | Vector algebra, fixed coordinate systems. | Tangent vectors, differential operators, parametrizations. |
| Benefits | Simplifies absolute measurement and comparison. | Captures local geometric behavior and directionality. |
Introduction to Base Points in Mathematics
Base points in mathematics serve as reference markers in geometric transformations, distinguishing crucial roles in coordinate systems and mapping functions. A fixed base point remains constant and is often chosen to simplify computations or define transformations like rotations and translations in Euclidean space. In contrast, a tangential base point moves along with the object, enabling the study of differential properties and tangents in manifold theory or calculus.
Defining Fixed Base Points
Fixed base points serve as precise reference locations in geospatial measurements, providing consistent coordinates that remain stable over time. These points enable accurate positioning and alignment in surveying, ensuring reliable data integration across mapping projects. Unlike tangential base points that adjust based on local context, fixed base points maintain absolute spatial consistency essential for long-term geodetic control.
Understanding Tangential Base Points
Tangential base points refer to locations on a geometric figure where a tangent line touches the curve without crossing it, crucial for defining direction and slope at that point. Unlike fixed base points, which serve as a static reference for transformations or measurements, tangential base points provide dynamic information about the curve's behavior and continuity. Understanding tangential base points is essential in differential geometry and computer graphics for accurately modeling curvature and ensuring smooth transitions.
Key Differences Between Fixed and Tangential Base Points
Fixed base points remain constant and do not move during measurement processes, providing stable reference coordinates and ensuring high accuracy in geodetic surveys. Tangential base points, on the other hand, are positioned along the tangent to a curve, allowing measurement adjustments in curved path applications such as railway or road alignments. The key difference lies in stability usage: fixed points serve as immovable origins for linear measurements, while tangential points adapt to angular changes, optimizing accuracy in curved geometries.
Applications of Fixed Base Points
Fixed base points are crucial in geodetic surveys and structural engineering for providing stable reference coordinates that ensure accuracy in measurements over time. These points facilitate precise monitoring of deformation in buildings, bridges, and other infrastructure by serving as immovable benchmarks. Tangential base points, on the other hand, are typically used for relative positioning in localized mapping where flexibility is prioritized over fixed spatial reference.
Applications of Tangential Base Points
Tangential base points are crucial in algebraic geometry and number theory, particularly for studying fundamental groups of algebraic curves where traditional base points are not available. They allow the definition of monodromy representations in cases involving punctured or singular curves, enhancing the analysis of etale fundamental groups and multiple zeta values. These points facilitate computations in Galois actions on fundamental groups, offering tools for research in anabelian geometry and arithmetic geometry.
Importance in Fundamental Group Calculations
The choice between a fixed base point and a tangential base point is crucial in fundamental group calculations as it influences the homotopy class identification of loops. Fixed base points provide a concrete reference that simplifies path composition and ensures well-defined group operations, while tangential base points enable handling cases where traditional base points may not exist, such as in algebraic geometry or when dealing with punctured spaces. Understanding their roles improves accuracy in computing p1, facilitating deeper insights into topological and geometric properties of spaces.
Role in Algebraic Topology and Geometry
In algebraic topology and geometry, fixed base points serve as constant reference points in fundamental group calculations and homotopy classes, ensuring consistent path concatenation and lifting properties. Tangential base points generalize this concept by replacing fixed points with tangent vectors, enabling the study of local geometric structures and monodromy representations in settings where canonical base points may not exist. The distinction enhances the flexibility of base point selection, facilitating deeper analysis in moduli spaces and algebraic curves.
Choosing the Right Base Point: Factors to Consider
Choosing the right base point between a fixed base point and a tangential base point depends on stability and precision requirements in machining or drafting processes. Fixed base points provide consistent reference for repeated measurements, ensuring high accuracy in static setups, while tangential base points offer flexibility for operations involving curved surfaces or rotational movements. Key factors include the nature of the workpiece geometry, required tolerances, and the specific application to optimize workflow efficiency.
Conclusion: Fixed vs Tangential Base Points
Fixed base points provide a stable and unchanging reference for measurements, ideal for consistent data collection in geodetic surveys, while tangential base points adjust dynamically based on local surface geometry, enhancing accuracy in curved or irregular terrains. The choice between fixed and tangential base points depends on the precision requirements and the nature of the area surveyed, with fixed points preferred for long-term stability and tangential points for adaptability. Selecting the appropriate base point type directly influences the reliability of spatial data and the effectiveness of mapping or engineering projects.
Fixed base point Infographic
 libterm.com
libterm.com