Singular homology is a fundamental tool in algebraic topology that measures the shape and structure of topological spaces by associating sequences of abelian groups or modules with them. It captures information about holes of various dimensions within a space by analyzing singular simplices and their boundaries. Explore the rest of this article to deepen your understanding of singular homology and its applications in topology.
Table of Comparison
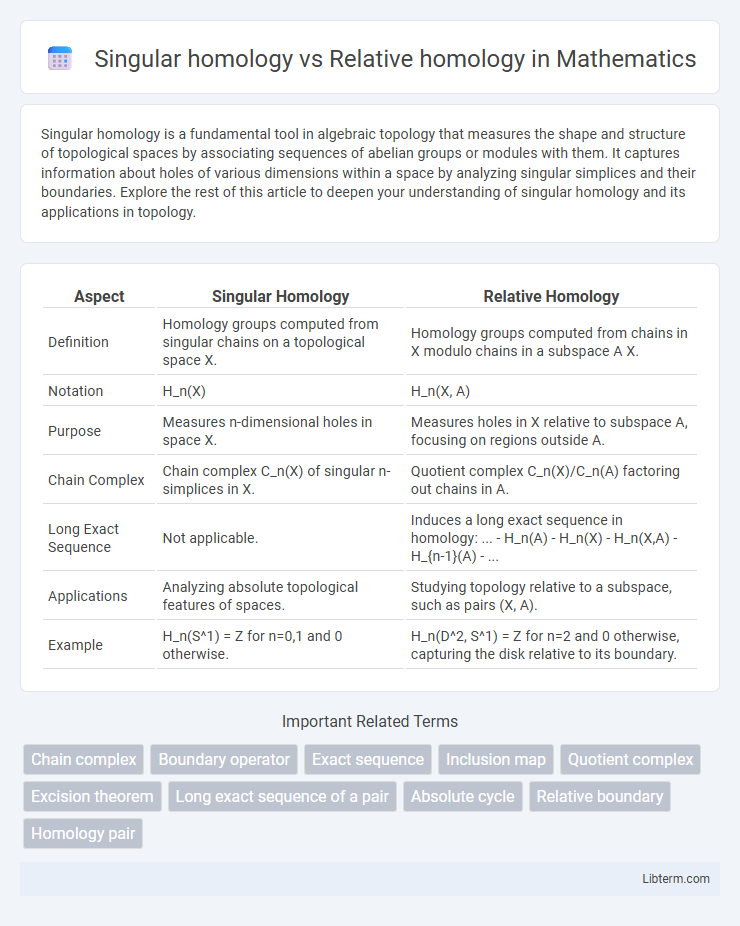
| Aspect | Singular Homology | Relative Homology |
|---|---|---|
| Definition | Homology groups computed from singular chains on a topological space X. | Homology groups computed from chains in X modulo chains in a subspace A X. |
| Notation | H_n(X) | H_n(X, A) |
| Purpose | Measures n-dimensional holes in space X. | Measures holes in X relative to subspace A, focusing on regions outside A. |
| Chain Complex | Chain complex C_n(X) of singular n-simplices in X. | Quotient complex C_n(X)/C_n(A) factoring out chains in A. |
| Long Exact Sequence | Not applicable. | Induces a long exact sequence in homology: ... - H_n(A) - H_n(X) - H_n(X,A) - H_{n-1}(A) - ... |
| Applications | Analyzing absolute topological features of spaces. | Studying topology relative to a subspace, such as pairs (X, A). |
| Example | H_n(S^1) = Z for n=0,1 and 0 otherwise. | H_n(D^2, S^1) = Z for n=2 and 0 otherwise, capturing the disk relative to its boundary. |
Introduction to Algebraic Topology
Singular homology assigns algebraic invariants to topological spaces by analyzing singular simplices and their boundary relations, providing a fundamental tool in algebraic topology. Relative homology extends this framework by considering pairs of spaces (X, A), capturing how the subspace A influences the homological structure of X. These concepts enable classification of topological spaces through homology groups, which play a crucial role in identifying holes and other topological features.
What is Singular Homology?
Singular homology is a fundamental tool in algebraic topology that assigns a sequence of abelian groups or modules to a topological space, capturing its essential shape and structure through continuous maps from standard simplices. It provides a means to classify and measure holes of different dimensions within the space by analyzing singular chains, cycles, and boundaries. Relative homology extends this concept by considering a topological space relative to a subspace, allowing the study of how the subspace influences the homological features of the whole.
Concept and Construction of Relative Homology
Relative homology extends singular homology by comparing topological spaces through pairs (X, A), where A is a subspace of X, capturing features of X that are not present in A. It is constructed using the quotient chain complex C_n(X)/C_n(A), leading to relative homology groups H_n(X, A) that measure the difference between the homology of X and A. This approach refines the classical singular homology by focusing on cycles in X modulo those in A, enabling the study of properties localized to the complement of A within X.
Key Differences Between Singular and Relative Homology
Singular homology measures the global topological features of a space by analyzing singular simplices mapped into it, while relative homology studies the relationship between a space and a subspace, capturing how features change when the subspace is removed. The singular homology groups H_n(X) classify n-dimensional holes in X alone, whereas the relative homology groups H_n(X, A) describe holes in X that are not present in the subspace A, providing finer topological distinctions. Computationally, relative homology uses exact sequences linking the homology of X, A, and the pair (X, A), facilitating analysis of spaces with complex inclusions.
Algebraic Formulation: Chains, Cycles, and Boundaries
Singular homology is defined using chains formed by formal sums of continuous maps from standard simplices into a topological space, with cycles representing chains whose boundary is zero and boundaries being images of higher-dimensional chains under the boundary operator. Relative homology generalizes this by considering chains in a space modulo chains in a subspace, leading to relative cycles whose boundaries lie within the subspace and relative boundaries that come from chains in the larger space. The algebraic formulation involves the quotient complex of chain groups \( C_n(X) / C_n(A) \), where \( A \subseteq X \), enabling the study of how homology changes relative to the inclusion of subspaces through exact sequences and boundary maps.
Exact Sequences in Singular and Relative Homology
Exact sequences in singular homology capture the relationship between homology groups of spaces and their subspaces, providing a powerful computational tool. The long exact sequence of a pair (X,A) links singular homology groups H_n(A), H_n(X), and relative homology groups H_n(X,A), encoding boundary maps and connecting homomorphisms essential for algebraic topology. This sequence enables the deduction of relative homology from known singular homologies, facilitating the analysis of topological structures and invariants.
Applications of Singular Homology
Singular homology provides a fundamental tool for analyzing topological spaces by associating sequences of abelian groups that reveal global geometric properties, crucial for classification problems in algebraic topology. It applies extensively in identifying holes and voids in spaces, aiding in fixed point theorems, and classifying manifolds via homology groups such as \(H_n(X)\). Relative homology extends these applications by measuring differences between spaces and subspaces, but singular homology remains pivotal for understanding intrinsic topological features, including invariants used in areas like data analysis and sensor networks.
Topological Applications of Relative Homology
Relative homology extends singular homology by analyzing pairs of topological spaces (X, A), capturing the homological features of X relative to a subspace A. It is essential in applications such as studying the homology of quotient spaces, excision theorems, and detecting holes or cycles that vanish within the subspace, providing finer invariants in complex spaces. Relative homology groups facilitate computations in manifold theory, algebraic topology, and Morse theory, especially when examining spaces with boundary or attaching cells.
Examples Illustrating Both Homology Types
Singular homology calculates topological invariants by associating chains of singular simplices to spaces like a circle S^1, where H_1(S^1) = Z captures the loop structure. Relative homology, exemplified by the pair (D^2, S^1) with the disk D^2 and its boundary circle S^1, measures how the boundary affects homology, yielding H_2(D^2, S^1) = Z reflecting the 2-dimensional filling. These examples illustrate singular homology's focus on absolute features of spaces and relative homology's role in quantifying how subspaces alter topological properties.
Conclusion: Choosing Between Singular and Relative Homology
Choosing between singular homology and relative homology depends on the topological context and the desired information. Singular homology effectively captures the global topological features of a space, while relative homology focuses on the relationship between a space and a subspace, highlighting boundary interactions and local structures. Employ singular homology for absolute invariants and relative homology when studying pairs or inclusions for more nuanced boundary and connectivity properties.
Singular homology Infographic
 libterm.com
libterm.com