Tensor product is a fundamental operation in mathematics and physics that combines two vectors, matrices, or tensors into a higher-dimensional tensor, preserving the structure of the original objects. It plays a crucial role in areas such as quantum mechanics, multilinear algebra, and computer science by enabling complex data representations and transformations. Explore the rest of this article to understand how the tensor product can enhance your knowledge and applications in various scientific fields.
Table of Comparison
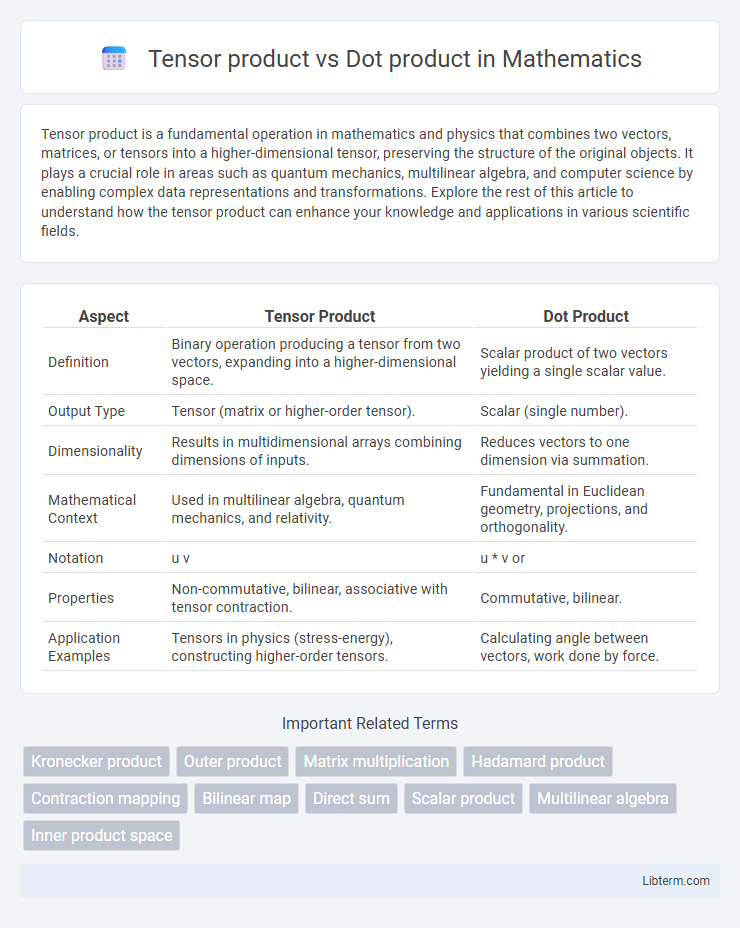
| Aspect | Tensor Product | Dot Product |
|---|---|---|
| Definition | Binary operation producing a tensor from two vectors, expanding into a higher-dimensional space. | Scalar product of two vectors yielding a single scalar value. |
| Output Type | Tensor (matrix or higher-order tensor). | Scalar (single number). |
| Dimensionality | Results in multidimensional arrays combining dimensions of inputs. | Reduces vectors to one dimension via summation. |
| Mathematical Context | Used in multilinear algebra, quantum mechanics, and relativity. | Fundamental in Euclidean geometry, projections, and orthogonality. |
| Notation | u v | u * v or |
| Properties | Non-commutative, bilinear, associative with tensor contraction. | Commutative, bilinear. |
| Application Examples | Tensors in physics (stress-energy), constructing higher-order tensors. | Calculating angle between vectors, work done by force. |
Introduction to Tensor and Dot Products
The tensor product combines two vectors into a higher-dimensional tensor, capturing multi-linear relationships and expanding the space of possible operations beyond simple scalar results. The dot product, also known as the scalar product, calculates a single scalar by summing the products of corresponding vector components, reflecting vector projection and similarity in Euclidean space. Understanding the tensor product versus the dot product is essential for applications in physics, machine learning, and multilinear algebra, where different types of tensor manipulations are required.
Mathematical Definitions
The dot product is a scalar-valued operation defined for two vectors \( \mathbf{a}, \mathbf{b} \in \mathbb{R}^n \), calculated as \( \mathbf{a} \cdot \mathbf{b} = \sum_{i=1}^n a_i b_i \), representing the sum of element-wise multiplications. The tensor product, also known as the outer product, of two vectors \( \mathbf{a} \in \mathbb{R}^m \) and \( \mathbf{b} \in \mathbb{R}^n \) produces an \( m \times n \) matrix defined by \( (\mathbf{a} \otimes \mathbf{b})_{ij} = a_i b_j \). Unlike the dot product yielding a scalar, the tensor product results in a higher-dimensional tensor capturing all pairwise multiplications between the vector components.
Key Differences Between Tensor and Dot Products
Tensor product creates a higher-dimensional array by combining vectors or matrices, resulting in a multidimensional tensor that encodes all pairwise interactions between elements. Dot product yields a scalar by multiplying corresponding entries of two vectors and summing the results, representing their magnitude correlation or projection. While tensor product increases dimensionality and stores comprehensive relational data, dot product reduces dimensionality to measure similarity or orthogonality.
Geometric Interpretation
The tensor product extends vectors into higher-dimensional spaces by combining their components without summation, resulting in a matrix or higher-order tensor that encodes directional relationships. The dot product, a scalar quantity, measures the cosine of the angle between two vectors, reflecting their projection and geometric alignment. Geometrically, the tensor product represents all possible pairwise interactions, while the dot product captures their linear overlap as a single value.
Applications in Mathematics and Physics
The tensor product allows for the construction of higher-dimensional vector spaces, essential in quantum mechanics for describing entangled states and multi-particle systems, while the dot product quantifies projections and work done by forces in classical mechanics. In mathematics, tensor products facilitate multilinear mappings and representation theory, whereas dot products serve as a fundamental tool in defining orthogonality and measuring angles in Euclidean spaces. Both operations underpin critical structures in differential geometry, with tensor products enabling the formulation of complex tensors and dot products assisting in metric definitions.
Role in Machine Learning and Deep Learning
The tensor product generalizes vector multiplication by creating higher-dimensional arrays essential for representing complex data structures in deep learning models, such as in convolutional layers and attention mechanisms. The dot product, a specific case of tensor operations, computes scalar similarity between vectors, playing a crucial role in neural network operations like weight updates and loss calculation. Efficient implementation of both products accelerates training and inference in large-scale machine learning systems, enhancing model expressiveness and performance.
Computational Complexity and Efficiency
The tensor product generates a higher-dimensional array by multiplying two vectors or matrices, resulting in a complexity of O(mn) for vectors of sizes m and n, which can quickly become computationally expensive for large inputs. In contrast, the dot product produces a scalar by summing pairwise element multiplications, with a linear complexity of O(n) for vectors of equal size n, making it much more efficient for large-scale computations. Efficient implementations of dot products leverage parallel processing and vectorized operations, whereas tensor products often require more memory and compute resources due to their expanded dimensionality.
Symbolic Notation and Representation
The tensor product is symbolized by the operator and produces a higher-dimensional array by combining two vectors or matrices, expanding their dimensionality without reducing them. The dot product, represented by a centered dot (*) or simply by juxtaposition, yields a scalar by summing the products of corresponding components of two vectors. In symbolic notation, the tensor product of vectors u R^m and v R^n is u v R^(mxn), whereas the dot product results in u * v R.
Common Pitfalls and Misconceptions
The tensor product and dot product are often confused, but they differ fundamentally: the tensor product combines two vectors into a higher-dimensional tensor, while the dot product results in a scalar by summing element-wise multiplications. A common pitfall is assuming the tensor product is commutative like the dot product, but swapping operands changes the structure of the output tensor. Misconceptions also arise when learners expect the tensor product to reduce dimensionality; instead, it increases dimensionality and preserves more information about the original vectors.
Summary and Practical Guidelines
The tensor product creates a higher-dimensional array representing all possible combinations of two vectors, widely used in quantum mechanics and multilinear algebra, while the dot product results in a scalar indicating the degree of similarity or projection between two vectors, essential in geometry and machine learning. Use the tensor product to construct complex state spaces or feature interactions, and apply the dot product for calculating angles, projections, or similarity metrics. Choosing between them depends on whether you need a scalar summary of vector alignment or an expanded representation capturing all interactions.
Tensor product Infographic
 libterm.com
libterm.com