A discrete measure assigns positive values only to countable sets, making it essential for analyzing phenomena concentrated at distinct points rather than over intervals. This concept plays a pivotal role in probability theory, statistical mechanics, and various branches of mathematics dealing with discrete data. Explore the rest of the article to understand how discrete measures apply to your field and their significant implications.
Table of Comparison
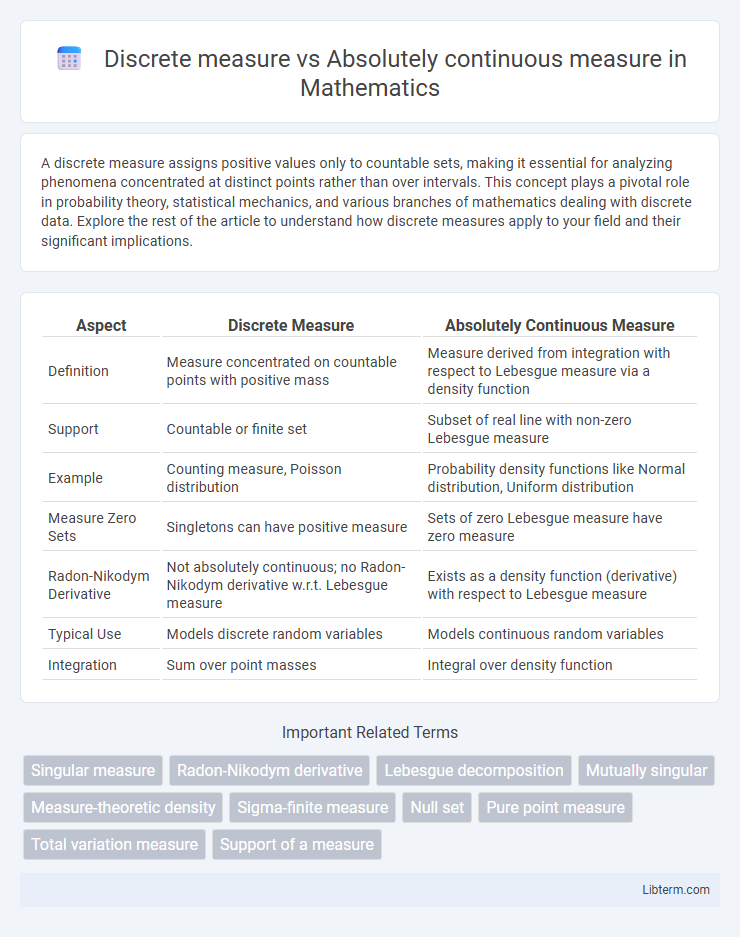
| Aspect | Discrete Measure | Absolutely Continuous Measure |
|---|---|---|
| Definition | Measure concentrated on countable points with positive mass | Measure derived from integration with respect to Lebesgue measure via a density function |
| Support | Countable or finite set | Subset of real line with non-zero Lebesgue measure |
| Example | Counting measure, Poisson distribution | Probability density functions like Normal distribution, Uniform distribution |
| Measure Zero Sets | Singletons can have positive measure | Sets of zero Lebesgue measure have zero measure |
| Radon-Nikodym Derivative | Not absolutely continuous; no Radon-Nikodym derivative w.r.t. Lebesgue measure | Exists as a density function (derivative) with respect to Lebesgue measure |
| Typical Use | Models discrete random variables | Models continuous random variables |
| Integration | Sum over point masses | Integral over density function |
Introduction to Measure Theory
Discrete measures assign positive measure to countable sets, often represented as sums of weighted Dirac delta functions, enabling precise quantification of isolated points. Absolutely continuous measures, characterized by the Radon-Nikodym derivative with respect to a reference measure like Lebesgue measure, capture distributions without singular points, allowing integration via density functions. Understanding the distinction between discrete and absolutely continuous measures is fundamental in measure theory for analyzing different types of measure spaces and their applications in probability and integration.
Defining Discrete Measures
Discrete measures are defined by assigning positive mass to countable sets, often represented as sums of weighted Dirac delta functions concentrated at distinct points. Each point in the support of a discrete measure has a positive measure, with the total measure being the sum of these point masses, enabling precise quantification of isolated outcomes in probability and measure theory. This contrasts with absolutely continuous measures, which are described by density functions relative to a reference measure like the Lebesgue measure.
Understanding Absolutely Continuous Measures
Absolutely continuous measures are defined with respect to another measure, typically the Lebesgue measure, such that if a set has measure zero in the reference, it also has measure zero under the absolutely continuous measure. This property is formalized by the Radon-Nikodym theorem, which guarantees the existence of a density function as the derivative of the absolutely continuous measure with respect to the reference measure. Unlike discrete measures that assign positive mass to isolated points, absolutely continuous measures distribute mass continuously over intervals, making them fundamental in probability theory and real analysis for modeling continuous random variables.
Key Differences Between Discrete and Absolutely Continuous Measures
Discrete measures assign positive probability only to countable sets, where each individual point has a nonzero measure; absolutely continuous measures, by contrast, are defined with respect to a reference measure like the Lebesgue measure and assign probability based on integrable density functions. Key differences include that discrete measures have probability mass functions (PMFs), while absolutely continuous measures possess probability density functions (PDFs). Moreover, discrete measures yield sums over countable points, whereas absolutely continuous measures require integration over continuous regions.
Mathematical Examples of Discrete Measures
Discrete measures assign positive mass to countable sets, such as the counting measure focused on integers or the Dirac delta measure centered at a single point. For example, the measure m defined by m({n}) = 1/n2 for n in N assigns weights to individual points, making it a classic discrete measure. This contrasts with absolutely continuous measures like the Lebesgue measure, which assigns volume continuously and vanishes on singletons.
Mathematical Examples of Absolutely Continuous Measures
Absolutely continuous measures can be exemplified by the Lebesgue measure on the real line, which assigns length to intervals in a way that corresponds to the integral of their indicator functions. Another example is any measure defined by a probability density function \( f(x) \), where the measure of a set \( A \) equals the integral \( \int_A f(x) \, dx \), illustrating absolute continuity with respect to the Lebesgue measure. Such measures contrast with discrete measures that assign positive mass only to countable sets without an underlying density function.
Applications of Discrete Measures
Discrete measures play a crucial role in statistics and probability, particularly in modeling phenomena with countable outcomes such as the number of events in a Poisson process or categorical data in surveys. They are extensively used in signal processing for representing quantized signals and in machine learning algorithms for handling discrete input features. These measures enable the computation of probabilities and expectations over discrete sample spaces, facilitating applications in reliability engineering, queuing theory, and natural language processing.
Applications of Absolutely Continuous Measures
Absolutely continuous measures play a crucial role in probability theory and statistics, especially in modeling continuous random variables via probability density functions (PDFs). They are widely applied in signal processing for representing noise distributions and in financial mathematics to model asset price dynamics through continuous stochastic processes like Brownian motion. These measures allow for differentiable transformations, enabling efficient computation of likelihoods and facilitating techniques such as parameter estimation and hypothesis testing in continuous data analysis.
Relationships and Interactions Between Measure Types
Discrete measures assign positive mass to isolated points, creating a countable sum of weighted atoms, while absolutely continuous measures spread mass continuously according to a density function with respect to the Lebesgue measure. Their interactions are characterized by the Lebesgue decomposition theorem, which states that any measure can be uniquely decomposed into the sum of a discrete measure and an absolutely continuous measure, along with a singular continuous component. This relationship enables the analysis of complex measures by examining the interplay of atomic contributions and smooth density distributions in measure theory and probability.
Summary and Practical Considerations
Discrete measures assign positive probability mass to countable points, making them ideal for modeling outcomes with distinct, isolated values such as counts or categorical data. Absolutely continuous measures are described by density functions relative to Lebesgue measure, suitable for modeling data varying continuously over an interval, like heights or weights. Practical considerations include choosing discrete measures for events with inherent gaps in the sample space and absolutely continuous measures when data exhibit smooth variation, with mixed measures applicable in scenarios combining discrete and continuous components.
Discrete measure Infographic
 libterm.com
libterm.com