Lie algebra is a fundamental structure in mathematics that studies algebraic operations capturing the essence of continuous symmetry and geometric transformations. It plays a crucial role in various fields, including theoretical physics, differential geometry, and control theory, providing tools to analyze the behavior of smooth manifolds and symmetry groups. Explore the rest of the article to deepen your understanding of Lie algebra's applications and properties.
Table of Comparison
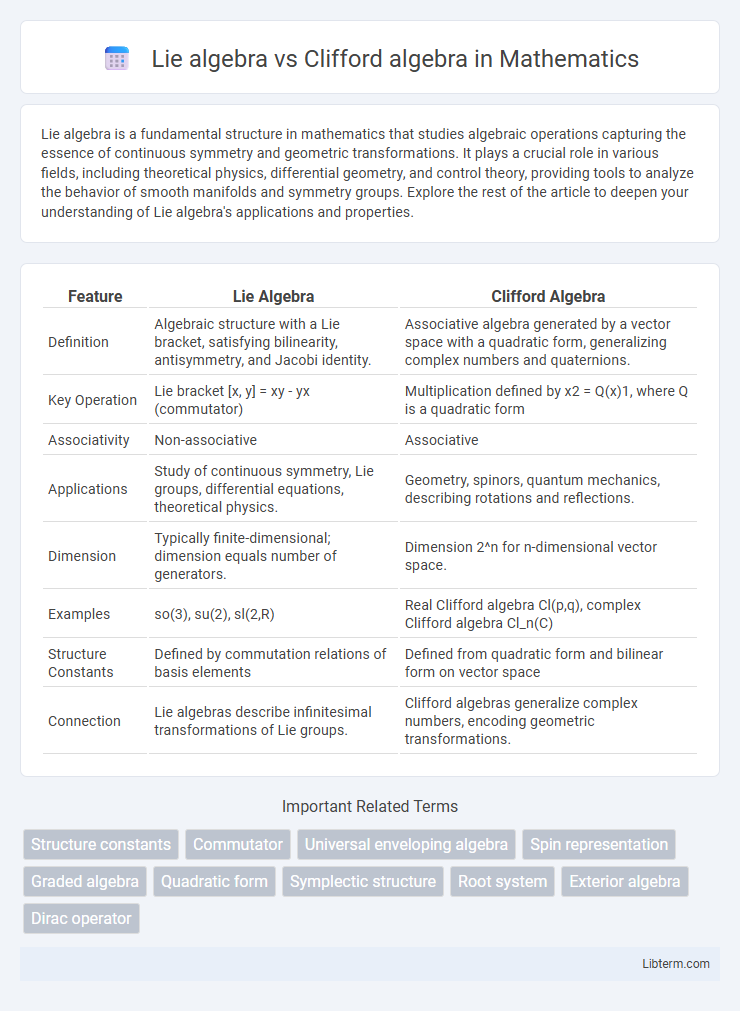
| Feature | Lie Algebra | Clifford Algebra |
|---|---|---|
| Definition | Algebraic structure with a Lie bracket, satisfying bilinearity, antisymmetry, and Jacobi identity. | Associative algebra generated by a vector space with a quadratic form, generalizing complex numbers and quaternions. |
| Key Operation | Lie bracket [x, y] = xy - yx (commutator) | Multiplication defined by x2 = Q(x)1, where Q is a quadratic form |
| Associativity | Non-associative | Associative |
| Applications | Study of continuous symmetry, Lie groups, differential equations, theoretical physics. | Geometry, spinors, quantum mechanics, describing rotations and reflections. |
| Dimension | Typically finite-dimensional; dimension equals number of generators. | Dimension 2^n for n-dimensional vector space. |
| Examples | so(3), su(2), sl(2,R) | Real Clifford algebra Cl(p,q), complex Clifford algebra Cl_n(C) |
| Structure Constants | Defined by commutation relations of basis elements | Defined from quadratic form and bilinear form on vector space |
| Connection | Lie algebras describe infinitesimal transformations of Lie groups. | Clifford algebras generalize complex numbers, encoding geometric transformations. |
Introduction to Lie Algebras and Clifford Algebras
Lie algebras are algebraic structures characterized by a bilinear, antisymmetric bracket operation satisfying the Jacobi identity, essential in studying continuous symmetries and differential equations. Clifford algebras generalize complex numbers and quaternions, constructed from a vector space with a quadratic form, enabling representation of geometric transformations and spinors. Both algebras underpin modern theoretical physics and geometry, with Lie algebras focusing on infinitesimal transformations and Clifford algebras on geometric and algebraic structures related to orthogonal groups.
Fundamental Concepts: Lie Algebra
Lie algebra is a mathematical structure primarily defined by a vector space equipped with a bilinear, antisymmetric bracket operation satisfying the Jacobi identity. This algebraic framework is fundamental in studying the infinitesimal symmetries of differentiable manifolds and Lie groups, enabling the classification of continuous transformation groups. Core concepts include the Lie bracket, structure constants, ideal theory, and representations, which are essential in theoretical physics and geometry.
Fundamental Concepts: Clifford Algebra
Clifford algebra extends the concept of vector spaces by integrating a quadratic form, generating an associative algebra that encodes geometric transformations and reflections. This algebra generalizes complex numbers and quaternions, providing a powerful framework for studying rotations, spinors, and multivectors in physics and geometry. Its construction involves generators satisfying specific anticommutation relations tied to the metric signature, enabling efficient representation of orthogonal groups and their algebras.
Historical Development and Mathematical Origins
Lie algebras, introduced by Sophus Lie in the late 19th century, originated from the study of continuous transformation groups and symmetries in differential equations, forming a fundamental tool in modern mathematical physics and geometry. Clifford algebras, developed by William Kingdon Clifford in the 1870s, emerged from efforts to generalize complex numbers and quaternions, providing an algebraic framework for quadratic forms and spinors. Both algebras have deeply influenced the structure theory of algebraic objects, with Lie algebras focusing on infinitesimal transformations and Clifford algebras on geometric and metric properties.
Structural Differences between Lie and Clifford Algebras
Lie algebras are defined by a bilinear, antisymmetric bracket operation satisfying the Jacobi identity, emphasizing the structure of infinitesimal transformations and symmetry. Clifford algebras, on the other hand, are associative algebras generated by a vector space with a quadratic form, allowing for the encoding of geometric properties through the Clifford product. The fundamental structural difference lies in Lie algebras being non-associative and centered on commutation relations, whereas Clifford algebras are associative and integrate both symmetric and antisymmetric components through their defining relations.
Applications in Mathematics and Physics
Lie algebras play a crucial role in mathematics and physics by describing the symmetry structures of differential equations and continuous transformation groups, particularly in quantum mechanics and particle physics. Clifford algebras provide a powerful framework for geometry and spinor calculus, underpinning the mathematical formulation of spacetime and Dirac operators in quantum field theory and relativity. Both algebras facilitate the study of symmetry and transformation but differ in their algebraic structures and applications, with Lie algebras focusing on infinitesimal symmetries and Clifford algebras emphasizing geometric and spin structures.
Representation Theory: A Comparative Overview
Lie algebras and Clifford algebras offer distinct yet interconnected frameworks in representation theory, where Lie algebra representations typically focus on homomorphisms into endomorphism algebras preserving the Lie bracket structure. Clifford algebras represent quadratic forms and provide spinor modules crucial for understanding spin representations, which naturally extend Lie algebra representations, especially for orthogonal Lie algebras. Their interplay is central in mathematical physics, with Clifford algebra's spin representations enriching the construction and classification of Lie algebra modules and deepening insights into symmetry and geometry.
Algebraic Operations and Properties
Lie algebras are characterized by their bilinear Lie bracket operation, which is antisymmetric and satisfies the Jacobi identity, enabling the study of infinitesimal symmetries and continuous transformation groups. Clifford algebras extend vector spaces by incorporating a quadratic form, producing a graded associative algebra with a product that generalizes the dot and wedge products, facilitating geometric interpretations and spinor constructions. While Lie algebras emphasize non-associative algebraic structures governing commutation relations, Clifford algebras provide associative frameworks crucial for applications in geometry, physics, and representation theory.
Interconnections and Interactions between Lie and Clifford Algebras
Lie algebras and Clifford algebras intertwine through their representation theory and algebraic structures, where Lie algebras often emerge as subalgebras within Clifford algebras via spinor constructions. The spin representation of a Lie algebra associated with a quadratic form leverages Clifford algebra modules, highlighting deep connections especially in studying orthogonal groups and spin groups. These interrelations facilitate the translation of geometric and algebraic problems across both frameworks, enriching areas like quantum mechanics, differential geometry, and theoretical physics.
Summary: Key Distinctions and Future Directions
Lie algebras, fundamental in describing continuous symmetries through commutation relations, differ from Clifford algebras, which encode geometric and quadratic form structures via anti-commutation relations. Key distinctions include Lie algebras' role in differential geometry and particle physics versus Clifford algebras' applications in spinor theory and quantum computing. Future research explores unifying frameworks leveraging both algebraic structures to advance quantum field theory and enhance computational models in theoretical physics.
Lie algebra Infographic
 libterm.com
libterm.com