Symmetry groups describe the set of all transformations that preserve an object's structure, capturing its geometric or algebraic invariances. These groups play a crucial role in fields like physics, chemistry, and mathematics by explaining patterns and conservation laws. Explore the full article to understand how symmetry groups shape your world and their applications across various disciplines.
Table of Comparison
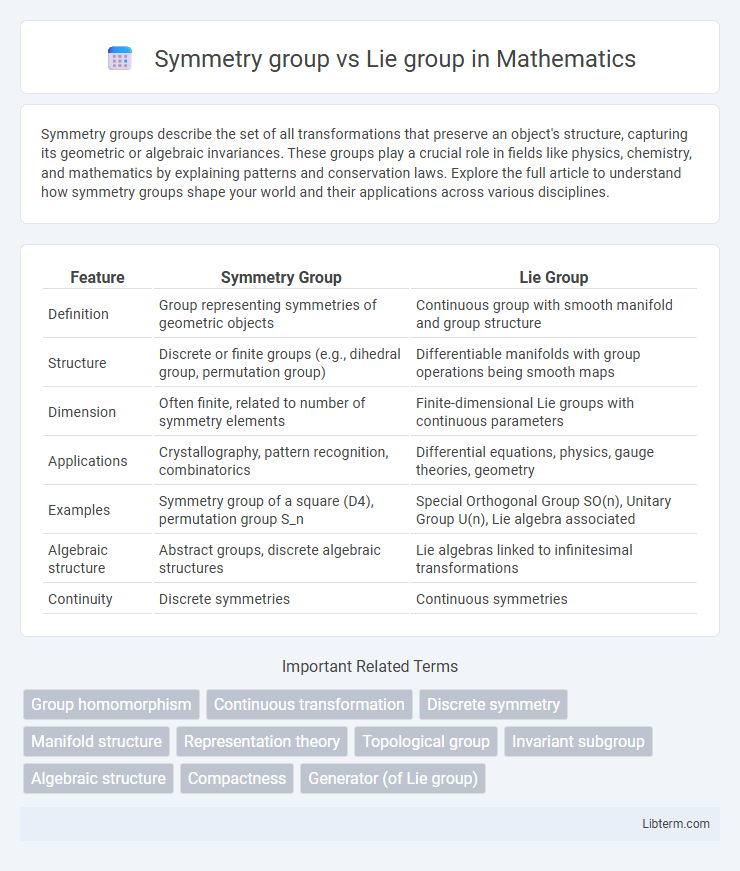
| Feature | Symmetry Group | Lie Group |
|---|---|---|
| Definition | Group representing symmetries of geometric objects | Continuous group with smooth manifold and group structure |
| Structure | Discrete or finite groups (e.g., dihedral group, permutation group) | Differentiable manifolds with group operations being smooth maps |
| Dimension | Often finite, related to number of symmetry elements | Finite-dimensional Lie groups with continuous parameters |
| Applications | Crystallography, pattern recognition, combinatorics | Differential equations, physics, gauge theories, geometry |
| Examples | Symmetry group of a square (D4), permutation group S_n | Special Orthogonal Group SO(n), Unitary Group U(n), Lie algebra associated |
| Algebraic structure | Abstract groups, discrete algebraic structures | Lie algebras linked to infinitesimal transformations |
| Continuity | Discrete symmetries | Continuous symmetries |
Introduction to Symmetry Groups and Lie Groups
Symmetry groups describe sets of transformations preserving the structure of geometric objects and are often finite or discrete, characterizing patterns and rigid motions in classical geometry. Lie groups extend this concept by incorporating continuous symmetries with differentiable manifold structures, enabling the study of smooth transformations and connecting algebraic groups with differential geometry. Introduction to Lie groups focuses on continuous symmetries like rotations and translations, essential in physics and advanced mathematics, while symmetry groups include permutations and reflections fundamental in discrete mathematics.
Defining Symmetry Groups: Concepts and Examples
Symmetry groups consist of discrete sets of transformations preserving the structure of geometric objects, exemplified by finite groups like the dihedral group representing polygon symmetries. Lie groups extend symmetry concepts to continuous transformations characterized by smooth manifolds and differentiable group operations, with classical examples such as the rotation group SO(3) and the general linear group GL(n, R). Defining symmetry groups involves understanding group actions on sets or spaces, where discrete symmetry groups handle finite or countable elements, and Lie groups address continuous symmetries linked to differential geometry and theoretical physics.
Introduction to Lie Groups: Structure and Fundamentals
Lie groups are smooth manifolds equipped with group operations that are differentiable, providing a continuous symmetry framework beyond discrete symmetry groups like symmetry groups of geometric objects. The structure of Lie groups combines algebraic properties with geometric intuition, governed by associated Lie algebras that capture infinitesimal transformations. Studying Lie groups involves understanding their manifold structure, group multiplication, and invariants, essential for applications in physics, differential equations, and advanced geometry.
Key Differences Between Symmetry Groups and Lie Groups
Symmetry groups primarily describe discrete transformations that preserve geometric objects, while Lie groups encompass continuous transformations characterized by smooth manifolds and differentiable structures. Symmetry groups are often finite or countable, representing operations like rotations or reflections, whereas Lie groups have an underlying algebraic structure that allows the use of calculus, exemplified by groups such as SO(3) or SU(2). The key difference lies in the mathematical framework: symmetry groups emphasize combinatorial properties, and Lie groups focus on continuous symmetries with differentiable group operations.
Algebraic Properties of Symmetry and Lie Groups
Symmetry groups, often finite or discrete, exhibit algebraic properties characterized by group operations such as composition and inverses, adhering to closure and associativity within permutation or geometric transformations. Lie groups, continuous and differentiable manifolds with group structures, combine algebraic properties of groups with smooth manifold theory, allowing for the study of infinitesimal generators via their Lie algebras. The interplay between algebraic structures of symmetry groups and the smooth, differentiable properties of Lie groups underpins powerful tools in mathematical physics and geometry.
Applications of Symmetry Groups in Science and Engineering
Symmetry groups provide a framework for analyzing geometric patterns and invariance in physical systems, playing a crucial role in crystallography, molecular chemistry, and materials science by classifying crystal structures and predicting molecular vibrations. Lie groups extend these concepts into continuous symmetries, essential for understanding conservation laws in physics and facilitating the formulation of gauge theories in particle physics. Engineering applications leverage symmetry groups to optimize mechanical designs, control robotic motion, and improve signal processing algorithms by exploiting symmetrical properties for increased efficiency and accuracy.
Lie Groups in Physics and Mathematics
Lie groups are continuous symmetry groups characterized by differentiable manifolds that combine group theory and differential geometry, essential in both physics and mathematics for describing smooth transformations. In physics, Lie groups underpin the formulation of fundamental symmetries in quantum mechanics and gauge theories, exemplified by groups like SU(2) for spin and SU(3) for the strong interaction. Mathematically, Lie groups facilitate the study of differential equations, topology, and geometry through their associated Lie algebras, enabling deep insights into the structure and classification of continuous symmetries beyond the discrete permutations described by symmetry groups.
Finite vs. Continuous Groups: Symmetry vs. Lie
Symmetry groups represent finite groups characterized by discrete transformations, such as rotations and reflections that preserve geometric objects, while Lie groups are continuous groups embodying smooth transformations parameterized by real variables, often describing symmetries in differential geometry and physics. Finite symmetry groups include examples like the dihedral group and permutation groups, whereas Lie groups encompass matrix groups such as SO(n), SU(n), and the Lorentz group, crucial in continuous symmetry and conservation laws. The fundamental difference lies in the discrete nature of finite groups versus the differentiable manifold structure of Lie groups, enabling continuous group operations and Lie algebra analysis.
Relationship and Interactions: Symmetry Groups and Lie Groups
Symmetry groups describe discrete or continuous transformations preserving geometric or algebraic structures, while Lie groups specifically refer to smooth manifolds with group operations that are differentiable. Lie groups provide a continuous framework that generalizes symmetry groups by integrating algebraic and topological properties, facilitating the study of continuous symmetries in physics and geometry. Interactions between these groups enable the classification of symmetry operations through Lie algebra representations, linking abstract group theory to differential geometry and theoretical physics.
Conclusion: Choosing Between Symmetry Groups and Lie Groups
Symmetry groups and Lie groups serve distinct purposes in mathematics and physics; symmetry groups are discrete and ideal for categorizing geometric objects with finite symmetries, while Lie groups are continuous and essential for analyzing smooth transformations in differential geometry and theoretical physics. The choice depends on the problem context: discrete symmetry groups apply to crystal structures and combinatorial problems, whereas Lie groups are crucial for understanding continuous symmetries in quantum mechanics and gauge theories. Selecting between them requires evaluating whether the system's symmetry involves discrete operations or continuous parameterized transformations.
Symmetry group Infographic
 libterm.com
libterm.com