Cellular automata are mathematical models consisting of a grid of cells that evolve through discrete time steps according to specific rules based on the states of neighboring cells. These systems can simulate complex patterns and processes found in nature, such as biological growth, fluid dynamics, and crystal formation. Explore the rest of the article to discover how cellular automata can help you understand and model dynamic systems.
Table of Comparison
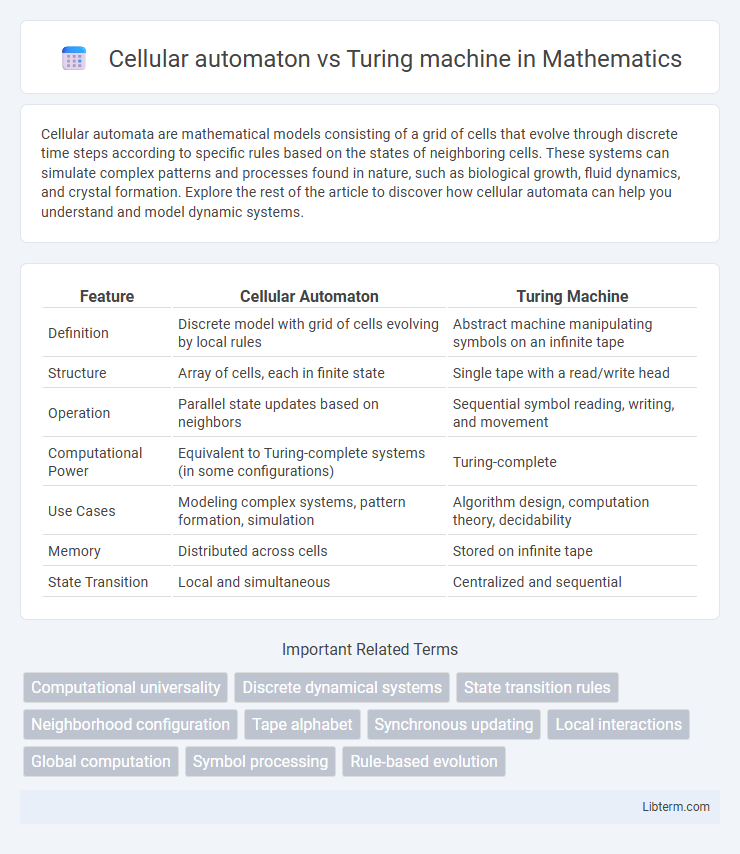
| Feature | Cellular Automaton | Turing Machine |
|---|---|---|
| Definition | Discrete model with grid of cells evolving by local rules | Abstract machine manipulating symbols on an infinite tape |
| Structure | Array of cells, each in finite state | Single tape with a read/write head |
| Operation | Parallel state updates based on neighbors | Sequential symbol reading, writing, and movement |
| Computational Power | Equivalent to Turing-complete systems (in some configurations) | Turing-complete |
| Use Cases | Modeling complex systems, pattern formation, simulation | Algorithm design, computation theory, decidability |
| Memory | Distributed across cells | Stored on infinite tape |
| State Transition | Local and simultaneous | Centralized and sequential |
Introduction to Cellular Automaton and Turing Machine
Cellular automata consist of a grid of cells evolving through discrete time steps according to a set of local rules based on the states of neighboring cells, enabling the modeling of complex systems with simple components. Turing machines operate through a tape of infinite length and a head that reads and writes symbols based on a finite set of rules, embodying a fundamental model of algorithmic computation. Both models serve as critical frameworks in theoretical computer science, with cellular automata illustrating parallel computation and Turing machines formalizing sequential computation processes.
Fundamental Concepts and Definitions
Cellular automata consist of a grid of cells, each in a finite number of states, evolving synchronously according to local rules based on neighboring cells, embodying parallel computation and spatial dynamics. Turing machines operate sequentially with an infinite tape and a head that reads and writes symbols based on a finite state control, representing a universal model for algorithmic computation. Both models capture computation's fundamentals but differ in structure: cellular automata emphasize distributed, local interactions while Turing machines emphasize sequential, global state transitions.
Historical Background and Development
Cellular automata, introduced by John von Neumann in the 1940s, were initially developed to model self-replicating systems and complex biological processes through discrete grids and local interaction rules. The Turing machine, conceptualized by Alan Turing in 1936, laid the foundational framework for algorithmic computation and formalized the concept of mechanical computation with an infinite tape and a read/write head. Both models significantly contributed to theoretical computer science, with the Turing machine influencing computational theory and complexity, while cellular automata advanced the study of emergent behavior and parallel computation.
Structural Differences Explained
Cellular automata consist of a grid of cells, each with a finite state updated simultaneously based on local rules, forming a decentralized and spatially structured computation model. Turing machines operate with a single tape manipulated by a read/write head, following a sequential and centralized state transition mechanism. The fundamental structural difference lies in cellular automata's parallel, spatially distributed architecture versus the Turing machine's linear, sequential control paradigm.
Computation Models Compared
Cellular automata and Turing machines represent fundamental computation models with distinct architectures and operational principles. While Turing machines utilize a linear tape for step-by-step symbol manipulation, cellular automata operate on grid-like arrays updating states based on local rules simultaneously across cells. The parallelism inherent in cellular automata contrasts with the sequential processing of Turing machines, affecting computational efficiency and applicability in modeling complex systems.
Universality and Computational Power
Cellular automata and Turing machines both exhibit universality, meaning they can simulate any computation given sufficient resources. Turing machines are the classical model of computation with a finite set of rules and an infinite tape, allowing step-by-step symbolic manipulation that underpins modern computability theory. Cellular automata, composed of discrete cells evolving simultaneously according to local rules, demonstrate equivalent computational power through complex pattern formation and state transitions, exemplified by Conway's Game of Life as a universal computational system.
Practical Applications in Science and Technology
Cellular automata model complex systems with simple rules, making them invaluable in simulating biological processes, fluid dynamics, and traffic flow, where spatial and temporal patterns emerge naturally. Turing machines provide a foundational framework for algorithm design and computation theory, critical in software development, cryptography, and formal verification of algorithms. Practical applications leverage cellular automata for parallel processing and pattern recognition, while Turing machines underpin the logical structure of modern computers and programming languages.
Limitations and Challenges
Cellular automata face limitations in simulating continuous processes and require extensive rule definitions to model complex systems, constraining their scalability and interpretability. Turing machines, despite their theoretical universality, encounter practical challenges such as infinite tape assumptions and computational resource constraints that hinder real-world applications. Both models struggle with issues of computational efficiency and complexity when addressing large-scale or highly detailed simulations.
Analogies and Key Distinctions
Cellular automata and Turing machines both serve as models of computation, leveraging discrete states and rule-based transitions to simulate complex systems. While Turing machines utilize an infinite tape and a head moving sequentially to perform computations, cellular automata operate on a grid of cells updating in parallel based on local neighbor states, emphasizing spatial dynamics. The key distinction lies in their computational frameworks: Turing machines focus on stepwise symbolic manipulation, whereas cellular automata highlight distributed processing and emergent global behavior from simple local interactions.
Future Directions and Research Opportunities
Research opportunities in cellular automata emphasize their potential to model complex systems and simulate natural phenomena at multiple scales, fostering advancements in computational biology and physics. Future directions for Turing machines involve exploring quantum and probabilistic variants to enhance computational power and address undecidable problems, bridging theoretical computer science with practical applications. Integrating cellular automaton frameworks with Turing machine architectures could lead to innovative hybrid models, optimizing problem-solving capabilities in artificial intelligence and algorithmic complexity.
Cellular automaton Infographic
 libterm.com
libterm.com