A weakly compact cardinal is a type of large cardinal in set theory characterized by its strong combinatorial and logical properties, including being inaccessible and satisfying the tree property. It plays a crucial role in higher-order logic and infinitary combinatorics, reflecting profound structural features of the mathematical universe. Explore the rest of this article to deepen your understanding of weakly compact cardinals and their significance.
Table of Comparison
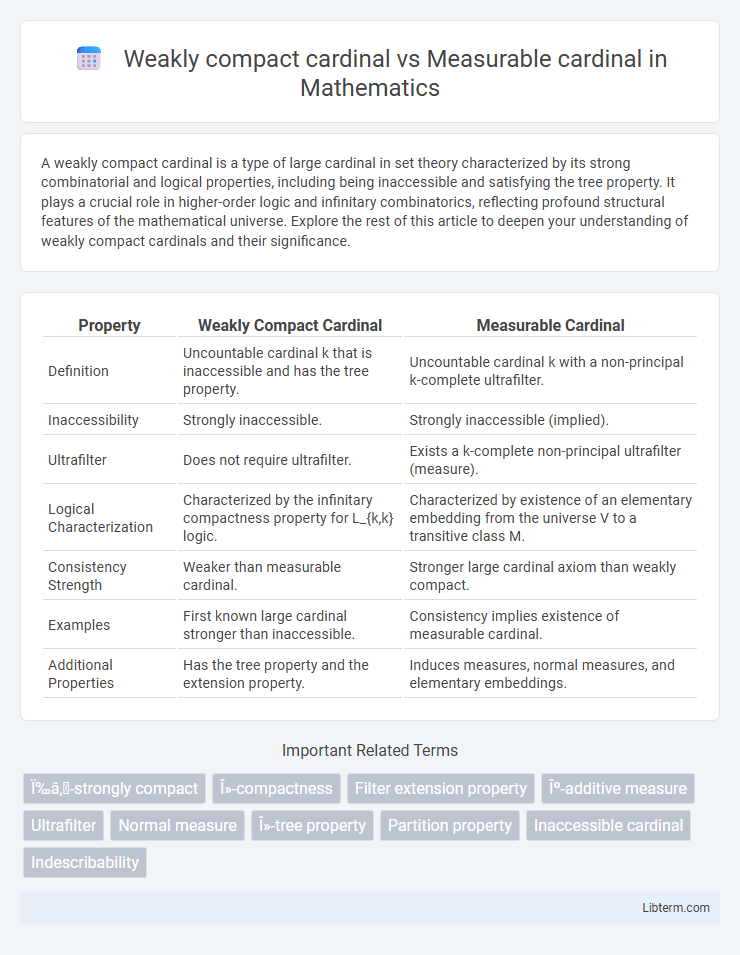
| Property | Weakly Compact Cardinal | Measurable Cardinal |
|---|---|---|
| Definition | Uncountable cardinal k that is inaccessible and has the tree property. | Uncountable cardinal k with a non-principal k-complete ultrafilter. |
| Inaccessibility | Strongly inaccessible. | Strongly inaccessible (implied). |
| Ultrafilter | Does not require ultrafilter. | Exists a k-complete non-principal ultrafilter (measure). |
| Logical Characterization | Characterized by the infinitary compactness property for L_{k,k} logic. | Characterized by existence of an elementary embedding from the universe V to a transitive class M. |
| Consistency Strength | Weaker than measurable cardinal. | Stronger large cardinal axiom than weakly compact. |
| Examples | First known large cardinal stronger than inaccessible. | Consistency implies existence of measurable cardinal. |
| Additional Properties | Has the tree property and the extension property. | Induces measures, normal measures, and elementary embeddings. |
Introduction to Large Cardinals
Weakly compact cardinals are large cardinals characterized by their strong combinatorial properties, such as the tree property and indescribability, making them natural generalizations of inaccessible cardinals. Measurable cardinals are stronger, equipped with a non-principal, k-complete ultrafilter, which enables the construction of elementary embeddings and has profound implications in set theory. Both types of cardinals are critical in the hierarchy of large cardinals, with measurable cardinals strictly extending the consistency strength and combinatorial properties of weakly compact cardinals.
Definition of Weakly Compact Cardinals
A weakly compact cardinal k is an uncountable regular cardinal that satisfies the tree property and the infinitary extension of the compactness theorem for first-order logic, meaning every k-complete filter can be extended to a k-complete ultrafilter. In contrast, a measurable cardinal k carries a non-principal k-complete ultrafilter, called a measure, which allows for the construction of ultrapowers and reflects stronger large cardinal properties. Weakly compact cardinals are thus characterized by combinatorial and logical compactness properties, whereas measurable cardinals are distinguished by the existence of a k-additive measure.
Definition of Measurable Cardinals
A measurable cardinal is an uncountable cardinal k equipped with a k-complete, non-principal ultrafilter, known as a measure, that allows for a fine-grained structure on subsets of k. This ultrafilter's k-completeness ensures closure under intersections of fewer than k sets, a stronger property than the weak compactness of a cardinal, which requires only certain combinatorial or logical compactness properties without the existence of such an ultrafilter. Measurable cardinals lie strictly above weakly compact cardinals in the large cardinal hierarchy due to their richer structural implications and the presence of a non-trivial, k-complete ultrafilter.
Key Properties of Weakly Compact Cardinals
Weakly compact cardinals are uncountable, strongly inaccessible, and defined by the tree property and the extension of certain combinatorial principles like the weak compactness of the infinitary language L_{k,k}. They lack a nontrivial k-complete ultrafilter, distinguishing them from measurable cardinals which possess a k-complete, nonprincipal ultrafilter that measures all subsets of k. Key properties of weakly compact cardinals include being k-indescribable and having the tree property that prohibits k-Aronszajn trees, making them critical in large cardinal hierarchy below measurability.
Key Properties of Measurable Cardinals
Measurable cardinals are large cardinals characterized by the existence of a non-principal, k-complete ultrafilter, which implies that every subset of the cardinal is measurable with respect to this ultrafilter. They possess a stronger combinatorial structure than weakly compact cardinals, including being inaccessible and reflecting stationary sets. Unlike weakly compact cardinals, measurable cardinals carry a highly nontrivial elementary embedding from the universe V into a transitive class M, revealing deep connections to inner model theory and large cardinal hierarchies.
Fundamental Differences Between the Two Cardinals
Weakly compact cardinals are defined by their combinatorial properties, including strong tree properties and being inaccessible, whereas measurable cardinals require the existence of a non-trivial, k-complete ultrafilter, enabling a measure on the cardinal. Measurable cardinals are strictly stronger in consistency strength, as every measurable cardinal is weakly compact, but the converse does not hold. The fundamental difference lies in the presence of a k-complete ultrafilter for measurable cardinals, which provides a stronger large cardinal property beyond the combinatorial characteristics of weakly compact cardinals.
Hierarchical Relationship in Set Theory
Weakly compact cardinals are a subset of large cardinals characterized by strong compactness and indescribability properties, but they lie strictly below measurable cardinals in the large cardinal hierarchy. Measurable cardinals possess a non-principal, k-complete ultrafilter, giving them greater consistency strength and stronger combinatorial properties than weakly compact cardinals. The hierarchical relationship is such that every measurable cardinal is weakly compact, but not every weakly compact cardinal is measurable, marking a clear distinction in their structural strength within set theory.
Consistency Strength and Equiconsistency
Weakly compact cardinals possess a lower consistency strength compared to measurable cardinals, with measurable cardinals implying the existence of a nontrivial k-complete ultrafilter that weakly compact cardinals do not necessarily have. The equiconsistency between these large cardinal notions does not hold, as measurable cardinals are strictly stronger in terms of consistency strength and imply the existence of weakly compact cardinals. In terms of consistency hierarchy, measurable cardinals imply significantly stronger combinatorial and structural properties than weakly compact cardinals, establishing a strict increase in consistency strength.
Applications in Mathematical Logic
Weakly compact cardinals are pivotal in model theory, enabling the construction of elementary embeddings and proving compactness results for infinitary languages \( L_{\kappa,\kappa} \). Measurable cardinals, equipped with a non-principal \(\kappa\)-complete ultrafilter, facilitate ultrapower constructions that yield strong elementary embeddings, critical for large cardinal hierarchy analyses and consistency proofs. Both cardinals significantly influence combinatorial set theory and descriptive set theory, with measurable cardinals providing stronger large cardinal assumptions impacting determinacy and inner model theory.
Open Questions and Research Directions
Weakly compact cardinals and measurable cardinals represent distinct large cardinal notions central to set theory, with measurable cardinals strictly stronger in consistency strength. Open questions include whether there exist models where a weakly compact cardinal exhibits properties typically associated with measurable cardinals or the precise interaction between these cardinals in inner model theory. Current research directions focus on refining the hierarchies of large cardinals, exploring forcing techniques to isolate characteristics of weak compactness versus measurability, and examining their roles in determinacy and descriptive set theory frameworks.
Weakly compact cardinal Infographic
 libterm.com
libterm.com