Isomorphism refers to a mapping between two structures that preserves their operations and relations, ensuring they are fundamentally identical in form despite superficial differences. This concept is essential in fields such as mathematics, computer science, and biology, where understanding structural similarities leads to deeper insights and practical applications. Explore the rest of the article to discover how isomorphism impacts various disciplines and your understanding of complex systems.
Table of Comparison
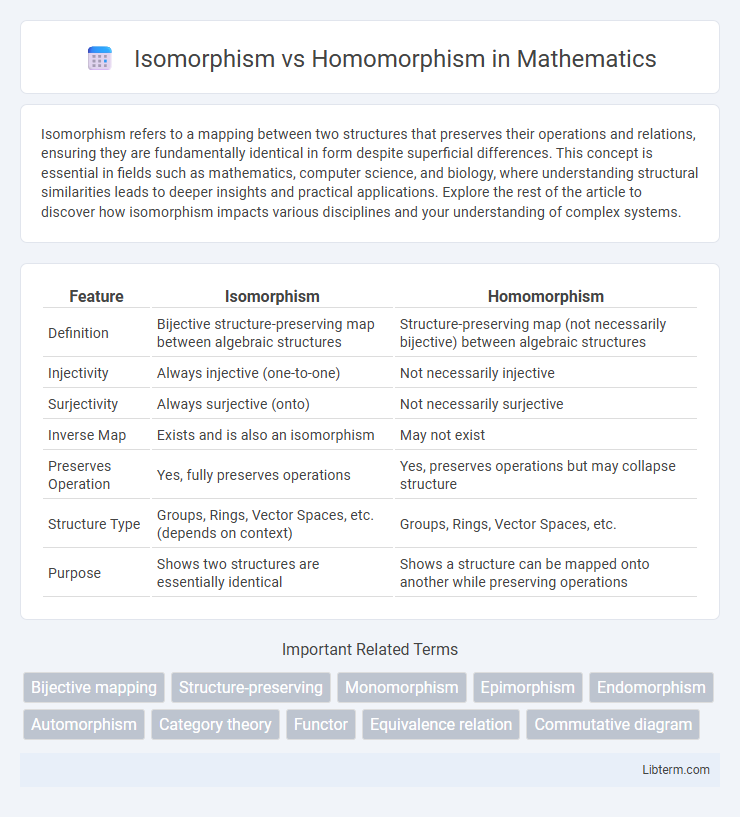
| Feature | Isomorphism | Homomorphism |
|---|---|---|
| Definition | Bijective structure-preserving map between algebraic structures | Structure-preserving map (not necessarily bijective) between algebraic structures |
| Injectivity | Always injective (one-to-one) | Not necessarily injective |
| Surjectivity | Always surjective (onto) | Not necessarily surjective |
| Inverse Map | Exists and is also an isomorphism | May not exist |
| Preserves Operation | Yes, fully preserves operations | Yes, preserves operations but may collapse structure |
| Structure Type | Groups, Rings, Vector Spaces, etc. (depends on context) | Groups, Rings, Vector Spaces, etc. |
| Purpose | Shows two structures are essentially identical | Shows a structure can be mapped onto another while preserving operations |
Introduction to Isomorphism and Homomorphism
Isomorphism and homomorphism are fundamental concepts in abstract algebra that describe structure-preserving mappings between algebraic systems. A homomorphism is a function between two algebraic structures, such as groups or rings, that respects the operation defined on these structures, ensuring the image of operation is the operation on the images. An isomorphism is a bijective homomorphism whose inverse is also a homomorphism, indicating that two algebraic structures are essentially identical in terms of their structure.
Defining Homomorphism in Mathematics
Homomorphism in mathematics is a structure-preserving map between two algebraic structures, such as groups, rings, or vector spaces, that respects the operations defined on them. Specifically, if \( f: A \to B \) is a homomorphism between groups \( A \) and \( B \), then for all elements \( x, y \in A \), the property \( f(x \cdot y) = f(x) \cdot f(y) \) holds, ensuring the operation is maintained under the mapping. Isomorphisms are a special type of homomorphism that are bijective and have inverses, making the two structures fundamentally identical in structure.
Understanding Isomorphism: Key Concepts
Isomorphism in mathematics defines a bijective mapping between two algebraic structures that preserves operations, ensuring that both structures exhibit identical properties and behaviors. This concept is crucial in group theory, ring theory, and graph theory, where isomorphic entities demonstrate structural equivalence despite possible differences in element labeling. Understanding isomorphism helps in classifying objects by their inherent patterns, facilitating the identification of fundamentally similar systems across various mathematical domains.
Main Differences Between Isomorphism and Homomorphism
Isomorphism and homomorphism differ primarily in structure preservation and reversibility; isomorphisms are bijective mappings that preserve operations and allow an inverse mapping, thereby establishing a structural equivalence between algebraic structures. Homomorphisms, however, are more general mappings that only require operation preservation without the necessity of being bijective or invertible, often resulting in a loss of information. The main difference lies in isomorphisms creating an exact correspondence, while homomorphisms permit structural transformations that may collapse elements.
Examples of Homomorphism in Algebra
Homomorphism in algebra is a structure-preserving map between two algebraic structures, such as groups, rings, or vector spaces, that respects the operations defined on them. A common example is the exponential map from the additive group of real numbers (R, +) to the multiplicative group of positive real numbers (R^+, x), defined by f(x) = e^x, which satisfies f(x + y) = f(x) * f(y). Another example includes the determinant function from the general linear group of nxn invertible matrices over a field to the multiplicative group of the field, where det(AB) = det(A)det(B), illustrating ring homomorphism properties.
Examples of Isomorphism in Algebra
Isomorphism in algebra is exemplified by the bijective correspondence between groups that preserves structure, such as the isomorphism between the additive group of integers modulo n (Z/nZ) and the group of nth roots of unity under multiplication. Another example includes the isomorphism between the vector space R^n and the space of all n-tuples of real numbers, showing identical dimension and linear structure. These instances highlight how isomorphic algebraic structures maintain operational compatibility and element relationships, distinguishing them from mere homomorphisms.
The Role of Structure Preservation
Isomorphism and homomorphism are fundamental concepts in abstract algebra that emphasize the role of structure preservation in mathematical mappings. Isomorphisms ensure a bijective correspondence between structures, preserving operations and properties exactly, which indicates that two algebraic structures are essentially the same in terms of their structure. Homomorphisms maintain the structure-preserving property for operations but may not be bijective, allowing for structural similarities without full equivalence.
Applications of Isomorphism and Homomorphism
Isomorphisms are essential in cryptography and network theory, enabling secure data encryption and efficient topology mapping by preserving structure exactly between algebraic systems. Homomorphisms find widespread use in coding theory and abstract algebra, allowing the transformation of complex algebraic expressions into simpler forms while maintaining operational relationships. Both concepts facilitate problem-solving in computer science, physics, and mathematics by providing frameworks for structure-preserving mappings and system equivalences.
Practical Implications in Computer Science
Isomorphism in computer science implies a one-to-one correspondence between data structures, ensuring perfect structural and functional similarity, which is crucial for tasks like database schema design and data migration. Homomorphism allows for structure-preserving mappings between algebraic structures, enabling optimization techniques in compiler design and efficient algorithms in cryptography. Understanding the distinction aids in choosing appropriate abstractions for software modeling, enhancing system interoperability and data integrity.
Conclusion: Choosing Between Isomorphism and Homomorphism
Choosing between isomorphism and homomorphism depends on the desired level of structural equivalence; isomorphisms establish a one-to-one correspondence preserving both operations and elements, indicating two algebraic structures are fundamentally identical. Homomorphisms, while preserving operation structure, allow more flexibility by mapping one structure into another without requiring bijection, making them suitable for analyzing substructure relations or simplifying complex systems. Selecting isomorphism ensures full structural equivalence, whereas homomorphism facilitates broader applications where exact equivalence is unnecessary.
Isomorphism Infographic
 libterm.com
libterm.com