Formally real fields are algebraic structures where the sum of squares cannot equal negative one, ensuring the preservation of order and positivity in mathematical operations. These fields play a crucial role in real algebraic geometry and the theory of ordered fields. Discover how this concept influences various areas of mathematics and why it matters for your understanding by reading the full article.
Table of Comparison
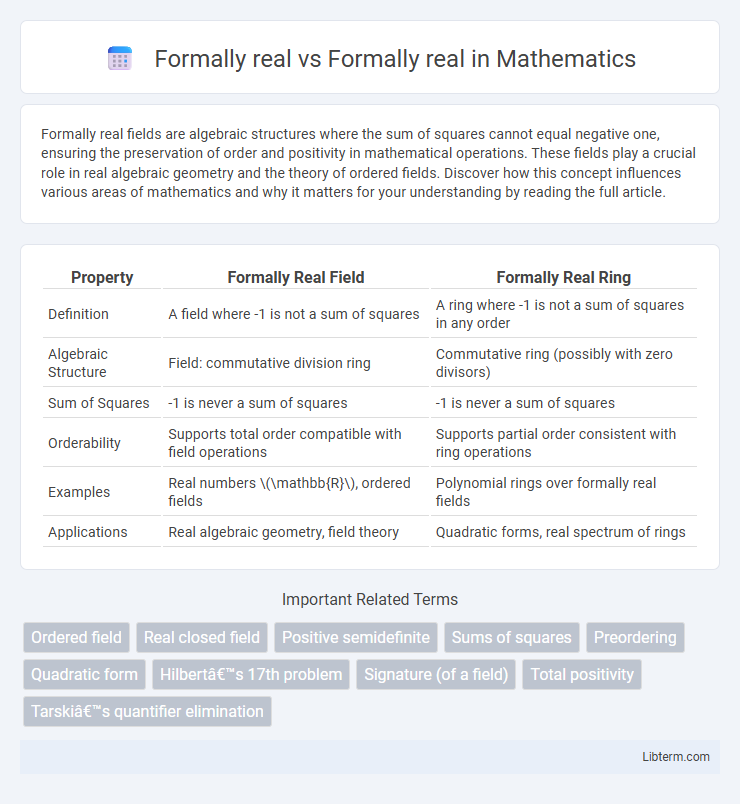
| Property | Formally Real Field | Formally Real Ring |
|---|---|---|
| Definition | A field where -1 is not a sum of squares | A ring where -1 is not a sum of squares in any order |
| Algebraic Structure | Field: commutative division ring | Commutative ring (possibly with zero divisors) |
| Sum of Squares | -1 is never a sum of squares | -1 is never a sum of squares |
| Orderability | Supports total order compatible with field operations | Supports partial order consistent with ring operations |
| Examples | Real numbers \(\mathbb{R}\), ordered fields | Polynomial rings over formally real fields |
| Applications | Real algebraic geometry, field theory | Quadratic forms, real spectrum of rings |
Introduction to Formally Real Fields
Formally real fields are characterized by the absence of an element whose square is the negative of one, allowing the definition of orderings compatible with field operations. These fields provide a foundational framework for understanding sums of squares and real algebraic geometry, contrasting with non-formally real fields where such orderings do not exist. The study of formally real fields centers on their role in fields admitting orderings and their connection to real closed fields.
Defining Formally Real: Key Concepts
Formally real fields are algebraic structures where -1 cannot be expressed as a sum of squares, ensuring the preservation of ordering properties crucial in real algebraic geometry. This key concept distinguishes formally real fields from non-formally real fields, where such sums exist. Understanding the definition and implications of formally real fields aids in the study of ordered fields, quadratic forms, and real closed fields.
Historical Background of Formally Real Fields
Formally real fields, introduced by Emil Artin in the early 20th century, arise from the need to generalize properties of real numbers through field theory, emphasizing orderability and positivity. The concept was crucial in understanding the algebraic structure where -1 cannot be expressed as a sum of squares, distinguishing formally real fields from non-real fields. Historical developments in real algebraic geometry and quadratic forms were deeply influenced by the characterization of formally real fields, shaping modern interpretations of ordered fields.
Formally Real vs. Real Closed Fields
Formally real fields are characterized by the property that -1 cannot be expressed as a sum of squares, enabling orderings consistent with the field operations. Real closed fields extend this concept by being formally real fields that are maximal with respect to ordering, meaning they have no proper algebraic extension that preserves the ordering. The distinction lies in real closed fields satisfying the intermediate value property for polynomials and admitting unique ordered field extensions, while formally real fields may lack these completeness properties.
Algebraic Properties of Formally Real Fields
Formally real fields are characterized by the absence of elements whose sum of squares equals -1, ensuring that -1 cannot be represented as a sum of squares within the field. This algebraic property guarantees the field admits an ordering compatible with its operations, making it an ordered field. The signature of quadratic forms over formally real fields is instrumental in classifying algebraic structures through real places and the Witt ring, highlighting their role in real algebraic geometry.
Characterizing Formally Real Fields Mathematically
Formally real fields are characterized by the absence of any element whose square sums to zero except the trivial case, ensuring no sum of squares equals -1 in the field. Mathematically, a field \( F \) is formally real if and only if \(-1\) is not expressible as a sum of squares, making \( F \) an ordered field compatible with its algebraic structure. The characterization relies on the existence of a compatible ordering and the positivity of squares, which distinguishes formally real fields from other field types where such ordering does not exist.
Formal Realness in Polynomial Equations
Formal realness in polynomial equations ensures that a polynomial ring allows no sum of squares to equal zero unless each square is zero, reflecting an essential property in real algebraic geometry. This concept distinguishes formally real fields, such as the real numbers, from non-formally real fields where negative squares can sum to zero, impacting the solvability of polynomial equations under ordered field constraints. Applications involve characterizing solution sets and symmetry properties in real polynomial systems, supporting advancements in optimization and real algebraic varieties.
Applications of Formally Real Fields
Formally real fields find crucial applications in real algebraic geometry, enabling the classification of orderings and the study of semi-algebraic sets. These fields support the theory of sums of squares, essential for optimization problems and Positivstellensatz results. In contrast, non-formally real fields lack orderings, limiting their use in real number-related applications but are significant in complex algebra and number theory.
Common Misconceptions About Formally Real
Common misconceptions about formally real fields include confusing them with real closed fields or assuming that the presence of an ordering implies the field is formally real. Formally real fields are specifically characterized by the property that -1 cannot be expressed as a sum of squares, which is distinct from merely having a real embedding or ordering. Understanding this nuance helps clarify that not all ordered fields are formally real, and not all formally real fields are real closed.
Summary: Distinguishing Formally Real from Related Concepts
Formally real fields are characterized by the property that -1 cannot be expressed as a sum of squares, distinguishing them from non-formally real fields where such representations exist. This key feature underpins their role in real algebraic geometry and quadratic form theory, contrasting with formally complex or p-adic fields that lack this restriction. Understanding these differences is essential for applications involving orderings on fields and real closed field classifications.
Formally real Infographic
 libterm.com
libterm.com