An isolated singularity is a point in a complex function where the function is not analytic, but is analytic in its immediate neighborhood except at that point. Understanding the different types of isolated singularities--removable, poles, and essential--helps in analyzing the behavior of complex functions near critical points. Explore the rest of the article to deepen your understanding of how isolated singularities impact complex analysis and function theory.
Table of Comparison
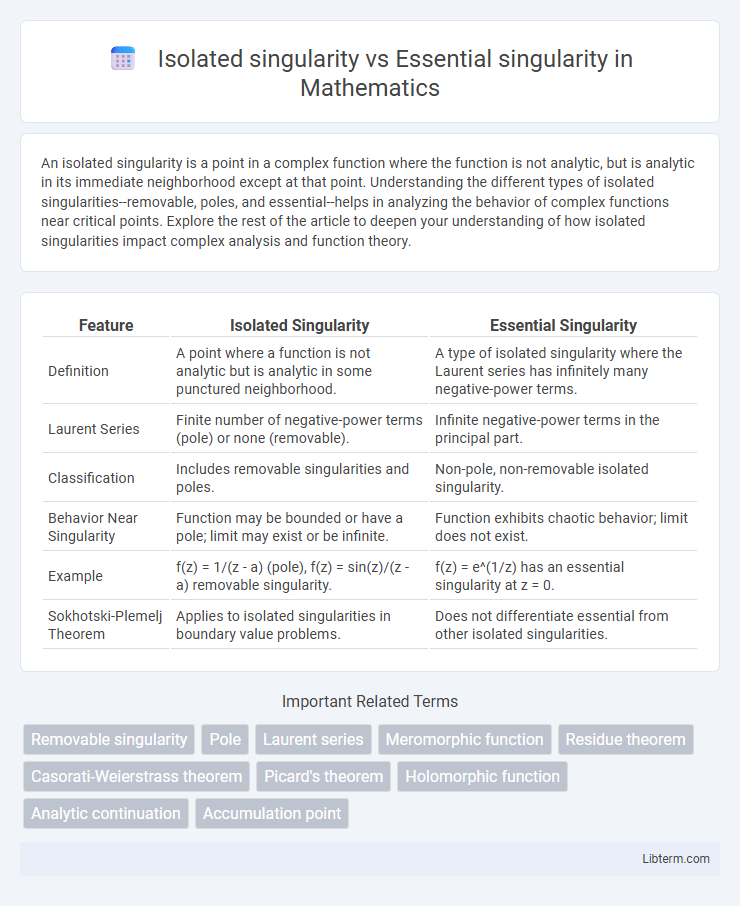
| Feature | Isolated Singularity | Essential Singularity |
|---|---|---|
| Definition | A point where a function is not analytic but is analytic in some punctured neighborhood. | A type of isolated singularity where the Laurent series has infinitely many negative-power terms. |
| Laurent Series | Finite number of negative-power terms (pole) or none (removable). | Infinite negative-power terms in the principal part. |
| Classification | Includes removable singularities and poles. | Non-pole, non-removable isolated singularity. |
| Behavior Near Singularity | Function may be bounded or have a pole; limit may exist or be infinite. | Function exhibits chaotic behavior; limit does not exist. |
| Example | f(z) = 1/(z - a) (pole), f(z) = sin(z)/(z - a) removable singularity. | f(z) = e^(1/z) has an essential singularity at z = 0. |
| Sokhotski-Plemelj Theorem | Applies to isolated singularities in boundary value problems. | Does not differentiate essential from other isolated singularities. |
Introduction to Complex Singularities
Isolated singularities in complex analysis occur at points where a function is not analytic but is analytic in some punctured neighborhood around that point. Essential singularities are a specific type of isolated singularity characterized by the function exhibiting highly erratic behavior, as described by the Casorati-Weierstrass theorem, near the singularity. Understanding the distinction aids in classifying singular points as removable, poles, or essential based on the nature of their Laurent series expansions.
Defining Isolated Singularities
Isolated singularities occur at points where a complex function is not analytic, but remains analytic in some punctured neighborhood around that point, distinguishing them from other types of singularities. Essential singularities are a subset of isolated singularities characterized by non-removable and highly irregular behavior, where the function exhibits infinitely oscillating values in every neighborhood of the point. Understanding isolated singularities is crucial in complex analysis, as they form the basis for classifying singular points into removable, poles, and essential singularities according to the nature of the Laurent series expansion.
Understanding Essential Singularities
Essential singularities occur at points where a complex function exhibits wildly oscillating values and fail to have a Laurent series with a finite principal part, distinguishing them from isolated singularities that are either removable or poles. The Casorati-Weierstrass theorem highlights that near an essential singularity, the function attains every complex value, with possibly one exception, infinitely often in every neighborhood. Understanding essential singularities is crucial for analyzing complex functions' behavior, especially in advanced fields like complex dynamics or quantum mechanics where the nature of singularities impacts convergence and solution properties.
Mathematical Characterization
Isolated singularities are points where a complex function is not analytic but is analytic in some punctured neighborhood around the point, classified into removable singularities, poles, or essential singularities based on the Laurent series expansion. Essential singularities exhibit neither a finite pole order nor removability, characterized by an infinite number of negative power terms in their Laurent series, causing the function's behavior to be highly oscillatory near the singularity. Mathematically, the Great Picard Theorem states that near an essential singularity, a function takes on every complex value, with at most one exception, infinitely often, contrasting with the predictable behavior near isolated poles or removable singularities.
Key Differences Between Isolated and Essential Singularities
Isolated singularities are points where a complex function is not analytic but is analytic in some punctured neighborhood around the point, whereas essential singularities exhibit highly irregular behavior near the point without a well-defined limit or residue. The key difference lies in the classification: isolated singularities include removable singularities and poles, while essential singularities cannot be removed or approximated by finite poles, often characterized by the Casorati-Weierstrass theorem. Functions with essential singularities display dense values near the singularity, making their behavior fundamentally distinct from isolated singularities that are poles or removable.
Examples of Isolated Singularities
Isolated singularities occur at points where a function is not analytic but is analytic in an arbitrarily small punctured neighborhood around that point, such as f(z) = sin(z)/z at z = 0, where the singularity is removable. Poles are another type of isolated singularity; for example, f(z) = 1/(z - 1) has a simple pole at z = 1. Essential singularities, in contrast, exhibit more complicated behavior exemplified by f(z) = e^(1/z) at z = 0, where the function's behavior near the point is highly oscillatory and cannot be removed or characterized as a pole.
Illustrative Cases of Essential Singularities
Essential singularities exhibit highly unpredictable behavior near the singular point, characterized by the Casorati-Weierstrass theorem where the function values densely populate the complex plane within every neighborhood. A classic illustrative case is the function f(z) = e^(1/z), which has an essential singularity at z = 0, demonstrating infinite oscillations and no limit as z approaches zero. Unlike isolated singularities such as poles, essential singularities cannot be removed or simplified, reflecting profoundly complex local function behavior.
The Role in Complex Analysis
Isolated singularities in complex analysis are points where a function is not analytic but is analytic in some punctured neighborhood, critical for classifying singular behavior into removable, poles, or essential types. Essential singularities, a subtype of isolated singularities, exhibit highly irregular function behavior characterized by the Casorati-Weierstrass theorem, where the function's values are dense in the complex plane near the singularity. Understanding isolated versus essential singularities is fundamental for residue calculus, analytic continuation, and mapping properties in complex function theory.
Theoretical and Practical Implications
Isolated singularities occur where a complex function fails to be analytic at a single point but remains analytic in a surrounding neighborhood, enabling classification into removable, poles, or essential types based on Laurent series expansion. Essential singularities present highly unpredictable behavior characterized by the Great Picard Theorem, which asserts that functions near such points take on nearly all complex values infinitely often, impacting complex dynamics and stability analysis. Practically, identifying whether a singularity is essential or isolated influences contour integration techniques and informs approaches in physics and engineering problems involving resonance and wave propagation.
Conclusion: Singularities in Complex Functions
Isolated singularities occur where a complex function is undefined yet remains analytic in a punctured neighborhood, classified further into removable, poles, or essential singularities based on their Laurent series. Essential singularities exhibit highly erratic behavior with infinitely many negative powers in the Laurent expansion, leading to extreme value distribution described by the Casorati-Weierstrass theorem. Understanding these distinctions is fundamental for analyzing complex functions' behavior near singular points and predicting function properties such as residue computation and analytic continuation.
Isolated singularity Infographic
 libterm.com
libterm.com