A linear operator is a mathematical function that maps elements from one vector space to another while preserving vector addition and scalar multiplication properties. Understanding linear operators is essential for solving systems of linear equations, transformations in quantum mechanics, and various applications in engineering. Explore the rest of this article to deepen your grasp of how linear operators impact your computational and theoretical work.
Table of Comparison
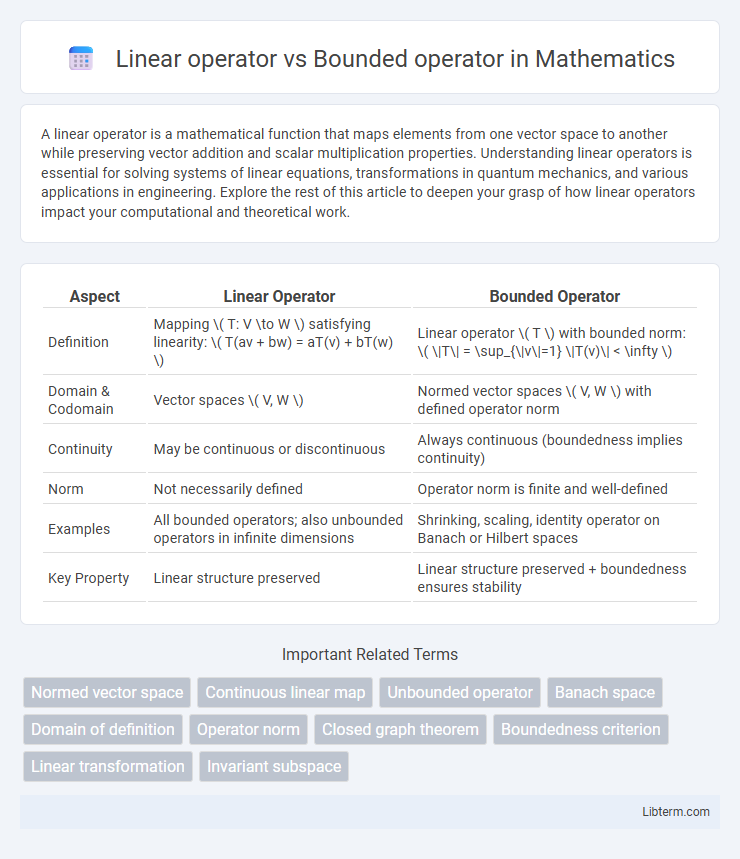
| Aspect | Linear Operator | Bounded Operator |
|---|---|---|
| Definition | Mapping \( T: V \to W \) satisfying linearity: \( T(av + bw) = aT(v) + bT(w) \) | Linear operator \( T \) with bounded norm: \( \|T\| = \sup_{\|v\|=1} \|T(v)\| < \infty \) |
| Domain & Codomain | Vector spaces \( V, W \) | Normed vector spaces \( V, W \) with defined operator norm |
| Continuity | May be continuous or discontinuous | Always continuous (boundedness implies continuity) |
| Norm | Not necessarily defined | Operator norm is finite and well-defined |
| Examples | All bounded operators; also unbounded operators in infinite dimensions | Shrinking, scaling, identity operator on Banach or Hilbert spaces |
| Key Property | Linear structure preserved | Linear structure preserved + boundedness ensures stability |
Introduction to Linear Operators
A linear operator is a mapping between vector spaces that preserves vector addition and scalar multiplication, fundamental in functional analysis. Bounded operators are a subset of linear operators characterized by the property that their operator norm is finite, ensuring continuity. Understanding these distinctions is crucial for analyzing operator behavior in normed spaces and applying them to solve linear equations efficiently.
Defining Bounded Operators
A bounded operator is a linear operator between normed vector spaces that maps bounded sets to bounded sets, ensuring continuity and stability in transformations. The operator norm quantifies the smallest bound such that for any vector x, the norm of the image is less than or equal to the operator norm multiplied by the norm of x. This boundedness condition guarantees the operator is continuous, making bounded operators central to functional analysis and operator theory.
Core Differences: Linear vs. Bounded Operators
A linear operator is a mapping between vector spaces that preserves vector addition and scalar multiplication, fundamentally defined by its linearity property. A bounded operator, a subtype of linear operators, ensures the existence of a finite constant bounding the operator norm, guaranteeing continuity and stability on normed vector spaces. Core differences lie in that all bounded operators are linear and continuous, whereas not all linear operators satisfy the boundedness criterion, particularly in infinite-dimensional spaces.
Mathematical Formulation of Linear Operators
A linear operator \( T: V \to W \) between vector spaces satisfies the properties \( T(\alpha x + \beta y) = \alpha T(x) + \beta T(y) \) for all vectors \( x, y \in V \) and scalars \( \alpha, \beta \). A bounded operator is a linear operator \( T \) between normed vector spaces for which there exists a constant \( M \geq 0 \) such that \( \|T(x)\|_W \leq M \|x\|_V \) for all \( x \in V \), ensuring continuity. The mathematical formulation highlights that all bounded operators are linear, but not all linear operators are bounded unless they satisfy the boundedness condition related to the operator norm.
Criteria for Operator Boundedness
An operator \(T: X \to Y\) between normed spaces is bounded if there exists a constant \(C \geq 0\) such that \(\|Tx\|_Y \leq C \|x\|_X\) for all \(x \in X\). The boundedness criterion is equivalent to continuity, meaning every bounded linear operator is continuous, but not all linear operators are bounded. In finite-dimensional spaces, all linear operators are bounded, whereas in infinite-dimensional spaces unbounded linear operators can exist, highlighting the importance of the boundedness condition.
Boundedness in Normed Vector Spaces
A bounded operator on a normed vector space is a linear operator for which there exists a constant C such that the norm of the operator applied to any vector does not exceed C times the norm of that vector. This boundedness condition ensures continuity and stability of the operator, making bounded operators a key class in functional analysis. Unlike general linear operators, bounded operators preserve the structure of normed spaces and allow the use of operator norms to measure their size.
Examples of Linear and Bounded Operators
Examples of linear and bounded operators include the identity operator on a normed vector space, which is both linear and bounded with norm one. Another example is the differentiation operator defined on the space of continuously differentiable functions, which is linear but unbounded under standard norms. The integral operator on continuous functions over a compact interval is linear and bounded, showcasing how boundedness depends on the operator's domain and codomain.
Significance in Functional Analysis
Linear operators serve as the foundational mappings between vector spaces, preserving vector addition and scalar multiplication, which is crucial for analyzing structure in functional analysis. Bounded operators, a subset of linear operators with finite operator norm, ensure continuity and stability, enabling the development of operator theory and spectral analysis. The distinction between linear and bounded operators is significant because boundedness guarantees well-posedness in infinite-dimensional spaces, facilitating the application of the Banach and Hilbert space frameworks.
Common Misconceptions and Pitfalls
Many mistakenly assume all linear operators are bounded, overlooking that unbounded linear operators frequently arise in infinite-dimensional spaces such as Hilbert or Banach spaces. Confusing boundedness with continuity can cause errors, since in normed vector spaces every bounded linear operator is continuous but not every linear operator is bounded or continuous. Recognizing that bounded operators maintain operator norm finiteness is essential to prevent misapplication in functional analysis and operator theory.
Conclusion: Choosing the Right Operator
Selecting the appropriate operator depends on the context: bounded operators guarantee continuity and stability in normed spaces, making them essential for practical applications in functional analysis. Linear operators, while more general, may lack boundedness, leading to instability or discontinuity that complicates analysis and solution methods. Prioritizing bounded operators ensures mathematical rigor and operational reliability in infinite-dimensional spaces.
Linear operator Infographic
 libterm.com
libterm.com