A symmetric monoidal category provides a mathematical framework where objects and morphisms can be combined using a tensor product that is associative, unital, and symmetric, meaning the order of objects in the tensor product does not affect the structure. This concept is fundamental in areas like quantum computing, topology, and theoretical computer science, as it allows the modeling of processes that are invariant under permutation. Explore the rest of this article to understand how symmetric monoidal categories enable elegant representations of complex systems and operations.
Table of Comparison
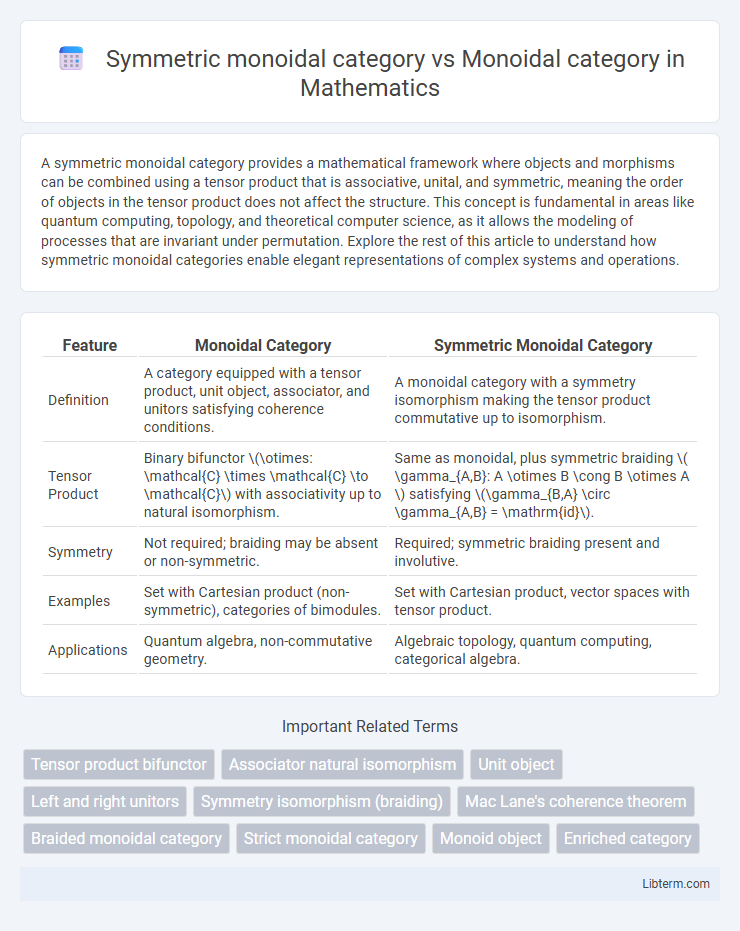
| Feature | Monoidal Category | Symmetric Monoidal Category |
|---|---|---|
| Definition | A category equipped with a tensor product, unit object, associator, and unitors satisfying coherence conditions. | A monoidal category with a symmetry isomorphism making the tensor product commutative up to isomorphism. |
| Tensor Product | Binary bifunctor \(\otimes: \mathcal{C} \times \mathcal{C} \to \mathcal{C}\) with associativity up to natural isomorphism. | Same as monoidal, plus symmetric braiding \( \gamma_{A,B}: A \otimes B \cong B \otimes A \) satisfying \(\gamma_{B,A} \circ \gamma_{A,B} = \mathrm{id}\). |
| Symmetry | Not required; braiding may be absent or non-symmetric. | Required; symmetric braiding present and involutive. |
| Examples | Set with Cartesian product (non-symmetric), categories of bimodules. | Set with Cartesian product, vector spaces with tensor product. |
| Applications | Quantum algebra, non-commutative geometry. | Algebraic topology, quantum computing, categorical algebra. |
Introduction to Monoidal Categories
Monoidal categories provide a framework in category theory where objects and morphisms are equipped with a tensor product and a unit object, enabling the study of compositional structures. Symmetric monoidal categories extend this framework by introducing a symmetry isomorphism that ensures the tensor product is commutative up to natural isomorphism, allowing for the interchangeability of factors in the tensor product. This added symmetry enables applications in fields such as algebra, quantum computing, and topological quantum field theory, distinguishing symmetric monoidal categories from general monoidal categories.
Fundamentals of Symmetric Monoidal Categories
Symmetric monoidal categories extend monoidal categories by incorporating a symmetry natural isomorphism that satisfies coherence conditions, enabling the interchangeability of tensor product factors. The fundamental structure involves objects and morphisms with an associative tensor product, unit object, and natural isomorphisms for associativity, unitality, and symmetry, formulated through commutative diagrams. This symmetry distinguishes symmetric monoidal categories by allowing the tensor product to be symmetric, crucial in areas like quantum computing and algebraic topology.
Key Differences: Monoidal vs Symmetric Monoidal
A monoidal category is a category equipped with a tensor product and an associativity constraint, allowing objects to be combined in a structured way, while a symmetric monoidal category additionally includes a symmetry isomorphism that guarantees the tensor product operation is commutative up to natural isomorphism. The key difference lies in the presence of the symmetry constraint, which ensures that swapping tensor factors does not affect the object structure, an essential property for modeling commutative phenomena in category theory and related fields. Symmetric monoidal categories are central in quantum computing, algebraic topology, and tensor calculus, where the order of tensoring is immaterial, whereas monoidal categories are more general and applicable in contexts without commutativity requirements.
Associativity and Unit Constraints
A symmetric monoidal category extends a monoidal category by including a symmetry isomorphism that makes the tensor product commutative up to isomorphism, while both share the core structure defined by associativity and unit constraints. Associativity in both categories is governed by a natural isomorphism \( \alpha_{A,B,C} : (A \otimes B) \otimes C \cong A \otimes (B \otimes C) \), satisfying the pentagon coherence condition to ensure consistent reassociation of tensor products. Unit constraints involve natural isomorphisms \( \lambda_A : I \otimes A \cong A \) and \( \rho_A : A \otimes I \cong A \) with the unit object \( I \), which satisfy the triangle coherence condition, maintaining coherence between unit and associativity isomorphisms in both symmetric and general monoidal categories.
The Role of the Symmetry Isomorphism
The symmetry isomorphism in a symmetric monoidal category provides a natural isomorphism that interchanges tensor factors, ensuring the braiding is involutive and satisfying coherence conditions like the hexagon axiom, which is absent in general monoidal categories. This symmetry enables equivalences such as \( A \otimes B \cong B \otimes A \) that hold strictly up to isomorphism, enhancing the structural flexibility for applications in areas like quantum computing and categorical algebra. Without the symmetry isomorphism, a monoidal category lacks this commutativity constraint, resulting in potentially non-symmetric braidings and less rigid tensor product behavior.
Examples of Monoidal Categories
Monoidal categories include examples such as the category of vector spaces with the tensor product, the category of sets with Cartesian product, and the category of chain complexes under tensor product. Symmetric monoidal categories extend monoidal categories by incorporating a symmetry isomorphism, evident in the category of vector spaces where the tensor product is commutative up to isomorphism. Categories like the category of topological spaces with Cartesian product or the category of finite sets also serve as examples of symmetric monoidal categories due to their inherent symmetry in the monoidal structure.
Examples of Symmetric Monoidal Categories
Symmetric monoidal categories are monoidal categories equipped with a symmetry isomorphism satisfying specific coherence conditions, making the tensor product commutative up to isomorphism. Examples include the category of vector spaces over a field with the tensor product, the category of sets with the Cartesian product, and the category of abelian groups under direct sum. These structures play a crucial role in areas like quantum computing, representation theory, and homological algebra.
Diagrammatic Representations
Symmetric monoidal categories feature diagrammatic representations where wires can cross, reflecting commutativity and symmetry axioms allowing the interchange of tensor factors. Monoidal categories, lacking this symmetry, use diagrams without wire crossings, emphasizing an ordered but associative tensor product. These visual distinctions clarify structural properties and coherence conditions unique to each category type.
Applications in Mathematics and Physics
Symmetric monoidal categories, characterized by a symmetry natural isomorphism allowing object interchange, find crucial applications in quantum computing and topological quantum field theory by modeling systems where particle exchange is indistinguishable. Monoidal categories, lacking symmetry constraints, are fundamental in algebraic topology and category theory for structuring tensor products and sequential composition without requiring commutativity. The distinction enables precise modeling of phenomena: symmetric structures capture entangled or interchangeable states in physics, while general monoidal categories describe non-symmetric process compositions in mathematical frameworks.
Summary and Further Reading
Symmetric monoidal categories are monoidal categories equipped with a symmetry isomorphism that satisfies naturality, coherence, and invertibility, allowing objects to commute under the tensor product, unlike general monoidal categories which lack this symmetry constraint. For deeper understanding, refer to "Categories for the Working Mathematician" by Saunders Mac Lane and the survey paper "Monoidal Categories" by Joyal and Street. Further exploration includes studying the role of symmetry in braided monoidal categories and its applications in quantum computing and topological quantum field theory.
Symmetric monoidal category Infographic
 libterm.com
libterm.com