The theta function is a special function in mathematics significant for its applications in number theory, complex analysis, and mathematical physics. It exhibits periodic behavior and is closely related to elliptic functions, modular forms, and the heat equation. Explore the rest of the article to discover how the theta function influences various scientific fields and why it matters for your understanding of advanced mathematics.
Table of Comparison
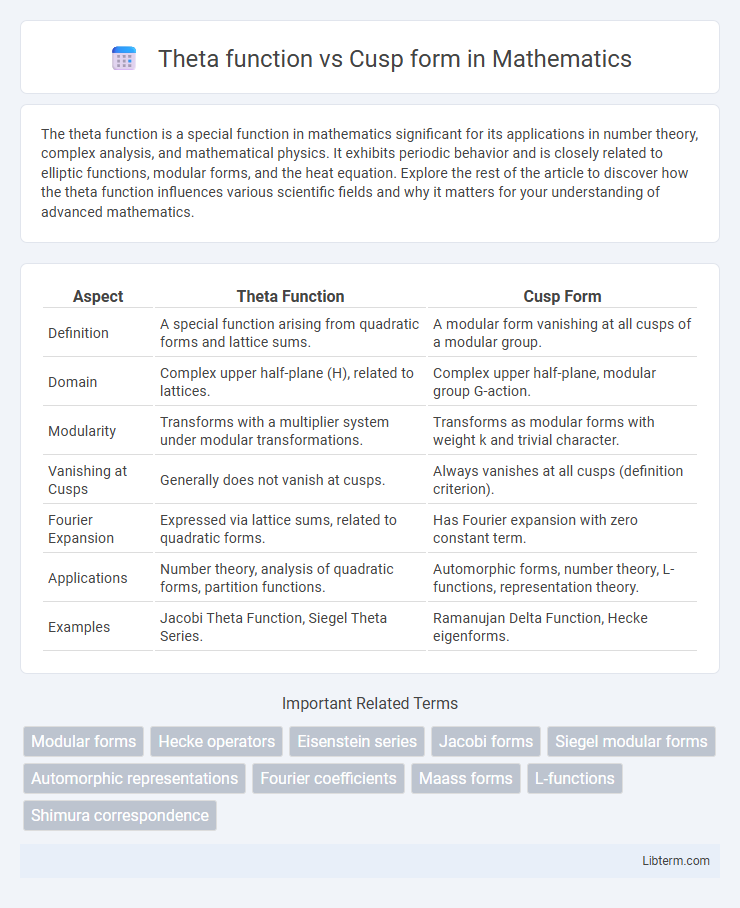
| Aspect | Theta Function | Cusp Form |
|---|---|---|
| Definition | A special function arising from quadratic forms and lattice sums. | A modular form vanishing at all cusps of a modular group. |
| Domain | Complex upper half-plane (H), related to lattices. | Complex upper half-plane, modular group G-action. |
| Modularity | Transforms with a multiplier system under modular transformations. | Transforms as modular forms with weight k and trivial character. |
| Vanishing at Cusps | Generally does not vanish at cusps. | Always vanishes at all cusps (definition criterion). |
| Fourier Expansion | Expressed via lattice sums, related to quadratic forms. | Has Fourier expansion with zero constant term. |
| Applications | Number theory, analysis of quadratic forms, partition functions. | Automorphic forms, number theory, L-functions, representation theory. |
| Examples | Jacobi Theta Function, Siegel Theta Series. | Ramanujan Delta Function, Hecke eigenforms. |
Introduction to Theta Functions and Cusp Forms
Theta functions arise as special functions in complex analysis and number theory, often representing generating functions for quadratic forms and modular forms of half-integral weight. Cusp forms are a subset of modular forms characterized by vanishing at all cusps of the modular curve, playing a crucial role in the theory of modular forms as they form the kernel of the constant term in Fourier expansions. Both concepts underpin deep relationships in automorphic forms, with theta functions frequently serving as explicit examples or building blocks for cusp forms in various arithmetic contexts.
Historical Background and Mathematical Significance
Theta functions, originating from the work of Carl Gustav Jacobi in the 19th century, played a pivotal role in the development of complex analysis and number theory by encoding lattice point distributions and modular transformations. Cusp forms emerged later as a crucial subset of modular forms, characterized by vanishing at all cusps and introduced through the work of mathematicians like Erich Hecke to study automorphic forms and L-functions. Both constructs have profound mathematical significance, with theta functions bridging quadratic forms and modularity, while cusp forms provide deep insights into the arithmetic of modular curves and the Langlands program.
Definitions: Theta Functions
Theta functions are special types of holomorphic functions arising from quadratic forms and lattice point counting, characterized by their transformation properties under modular transformations of the upper half-plane. They often encode the number of representations of integers by quadratic forms and serve as building blocks in the theory of modular forms. Unlike cusp forms, which vanish at cusps of modular curves, theta functions typically have explicit Fourier expansions with non-vanishing constant terms, reflecting their geometric and arithmetic significance.
Definitions: Cusp Forms
Cusp forms are a special class of modular forms that vanish at all the cusps of the modular curve, meaning their Fourier expansion lacks constant terms at infinity. These analytic functions on the upper half-plane exhibit rapid decay toward cusps, ensuring square-integrability on the fundamental domain of the modular group. Unlike general theta functions, cusp forms encode deep arithmetic information and are critical in the theory of automorphic forms and number theory.
Fundamental Differences Between Theta Functions and Cusp Forms
Theta functions are special types of modular forms characterized by their explicit construction via quadratic forms and typically exhibit nonzero Fourier coefficients at the cusp, reflecting lattice counting properties. Cusp forms are modular forms that vanish at all cusps, implying their Fourier expansions lack constant or lower-order terms, representing more subtle automorphic behaviors. The fundamental difference lies in the vanishing behavior at cusps: theta functions generally do not vanish and encode arithmetic geometry data directly, while cusp forms vanish and capture deeper spectral properties of modular forms.
Analytic Properties and Transformation Laws
Theta functions exhibit modular transformation laws characterized by specific multiplier systems tied to their lattice structures, reflecting their periodicity and quasi-periodicity in the complex plane. Cusp forms, as holomorphic modular forms vanishing at cusps, demonstrate analytic properties including rapid decay at infinity and satisfy transformation laws under the modular group with precise weight and character. The analytic distinction lies in cusp forms' zero boundary behavior contrasting theta functions' non-vanishing growth, while both maintain strict modular transformation symmetries crucial for automorphic form theory.
Applications in Number Theory and Modular Forms
Theta functions serve as generating functions encoding number-theoretic information such as representation of integers by quadratic forms, playing a critical role in constructing modular forms with explicit Fourier coefficients. Cusp forms, characterized by vanishing constant terms at cusps, encapsulate deep arithmetic properties including eigenvalues of Hecke operators, crucial for understanding L-functions and automorphic representations. Both entities underpin advanced structures in number theory by linking quadratic forms, elliptic curves, and Galois representations through the framework of modular forms.
Connections to Automorphic Forms
Theta functions serve as explicit examples of automorphic forms, often arising from quadratic forms and encoding arithmetic information through their Fourier coefficients. Cusp forms are a subclass of automorphic forms characterized by rapid decay at cusps, contributing to the spectral decomposition of automorphic representations. The interplay between theta functions and cusp forms illuminates the structure of the automorphic spectrum and the theory of modular forms, facilitating advances in number theory and representation theory.
Recent Developments and Research Trends
Recent developments in the study of Theta functions and Cusp forms have emphasized their roles in modern number theory and automorphic forms, with significant progress in understanding their Fourier coefficients and modular transformations. Research trends highlight the interplay between Theta functions as generating series of quadratic forms and Cusp forms as eigenfunctions of Hecke operators, facilitating advances in Langlands program and arithmetic geometry. Computational techniques and p-adic analysis have become pivotal in exploring explicit correspondences and lifting constructions between these classes of modular objects.
Conclusion: Choosing Between Theta Functions and Cusp Forms
Choosing between theta functions and cusp forms depends on the desired properties in modular form analysis; theta functions often provide explicit formulae with connections to quadratic forms and lattice sums, while cusp forms exhibit stronger vanishing conditions at cusps, useful in number theory and arithmetic geometry. Theta functions are typically simpler to construct and analyze, making them suitable for explicit computations and generating functions. Cusp forms, however, play a critical role in the theory of modular forms with deep implications in the Langlands program, elliptic curves, and automorphic representations.
Theta function Infographic
 libterm.com
libterm.com