Theta functions are special functions of several complex variables that arise in various branches of mathematics and physics, particularly in number theory, combinatorics, and string theory. These functions exhibit remarkable transformation properties under modular transformations and play a crucial role in the theory of elliptic functions and modular forms. Explore the rest of this article to uncover how theta functions can enrich your understanding of advanced mathematical concepts.
Table of Comparison
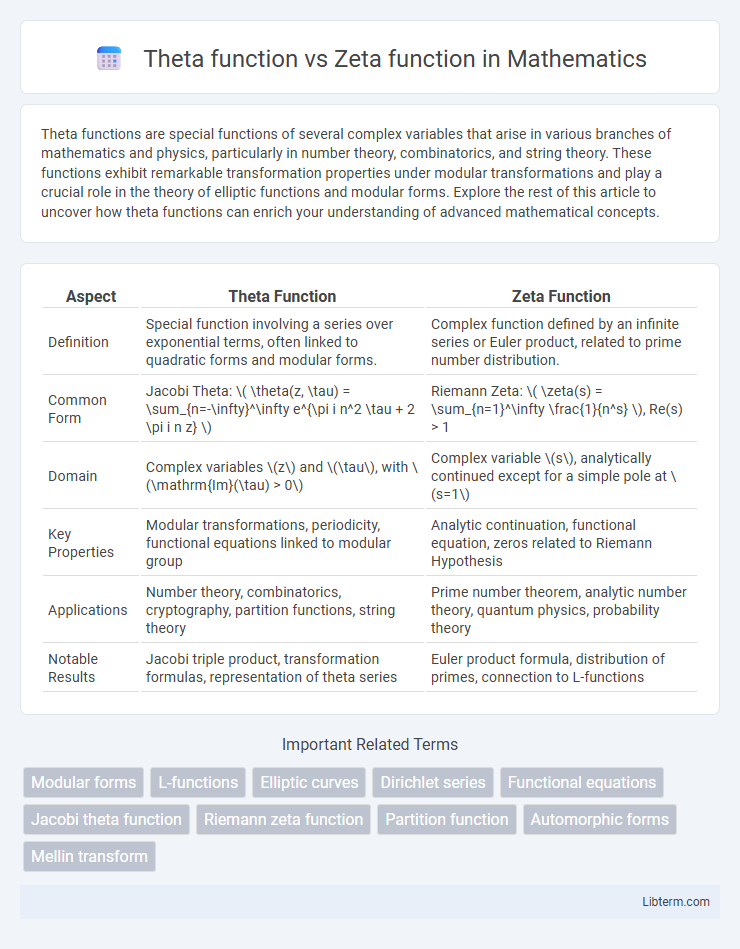
| Aspect | Theta Function | Zeta Function |
|---|---|---|
| Definition | Special function involving a series over exponential terms, often linked to quadratic forms and modular forms. | Complex function defined by an infinite series or Euler product, related to prime number distribution. |
| Common Form | Jacobi Theta: \( \theta(z, \tau) = \sum_{n=-\infty}^\infty e^{\pi i n^2 \tau + 2 \pi i n z} \) | Riemann Zeta: \( \zeta(s) = \sum_{n=1}^\infty \frac{1}{n^s} \), Re(s) > 1 |
| Domain | Complex variables \(z\) and \(\tau\), with \(\mathrm{Im}(\tau) > 0\) | Complex variable \(s\), analytically continued except for a simple pole at \(s=1\) |
| Key Properties | Modular transformations, periodicity, functional equations linked to modular group | Analytic continuation, functional equation, zeros related to Riemann Hypothesis |
| Applications | Number theory, combinatorics, cryptography, partition functions, string theory | Prime number theorem, analytic number theory, quantum physics, probability theory |
| Notable Results | Jacobi triple product, transformation formulas, representation of theta series | Euler product formula, distribution of primes, connection to L-functions |
Introduction to Theta and Zeta Functions
Theta functions, originating from complex analysis and number theory, are special functions characterized by their periodicity and transformation properties, playing a crucial role in elliptic functions, modular forms, and partition theory. Zeta functions, including the Riemann zeta function, are complex functions defined as infinite series or products with deep connections to prime number distribution, analytic number theory, and mathematical physics. Both functions exhibit rich analytic structures and symmetry properties, with applications ranging from cryptography to quantum chaos and string theory.
Historical Development of Theta and Zeta Functions
The historical development of Theta and Zeta functions traces back to pioneering work by mathematicians such as Leonhard Euler and Carl Gustav Jacobi in the 18th and 19th centuries. The Theta function, originating from Jacobi's study of elliptic functions, became crucial in analyzing quadratic forms and modular forms, while the Zeta function, introduced by Bernhard Riemann in 1859, revolutionized analytic number theory through its connections to prime number distribution. Both functions have profoundly influenced modern mathematics, underpinning deep theories in number theory, complex analysis, and mathematical physics.
Mathematical Definitions: Theta vs Zeta
The Theta function, often represented as th(z, t), is a special function defined by an infinite series involving complex variables, primarily used in number theory and combinatorics to describe periodicities and modular forms. The Zeta function, notably the Riemann Zeta function z(s), is defined as a complex series sum z(s) = n=1 to 1/n^s for complex numbers s with real part greater than 1, playing a central role in the distribution of prime numbers and analytic number theory. While the Theta function encodes properties of lattices and heat distribution, the Zeta function analyzes the distribution of prime numbers through its nontrivial zeros.
Key Properties and Formulations
The Theta function, often represented as th(z; t), is characterized by its quasi-periodicity and modular transformation properties, defined through an infinite series summing over integer squares, essential in heat equation solutions and elliptic function theory. The Zeta function, particularly the Riemann Zeta function z(s), is defined via an infinite series over natural numbers raised to the power s and extends to a meromorphic function with a simple pole at s = 1, playing a crucial role in analytic number theory and the distribution of prime numbers. Both functions exhibit functional equations linking values at s and 1 - s for Zeta, and transformations under modular group actions for Theta, highlighting their deep connections in complex analysis and number theory.
Applications in Number Theory
Theta functions play a crucial role in number theory by encoding representation numbers of quadratic forms and facilitating the study of modular forms, which are essential in understanding partition functions and integer solutions to Diophantine equations. Zeta functions, particularly the Riemann zeta function, are fundamental tools for analyzing the distribution of prime numbers and formulating conjectures related to the zeros of complex functions impacting prime number theory. Both functions provide deep insights into arithmetic properties and have applications in advanced topics like the proof of the prime number theorem and the theory of elliptic curves.
Analytical Continuation and Functional Equations
The Theta function's analytical continuation involves extending its domain through the Poisson summation formula, revealing deep connections with modular forms, and its functional equation reflects self-invariance under modular transformations. In contrast, the Zeta function's analytic continuation is achieved via the appropriate use of the Euler-Maclaurin formula and Mellin transforms, extending the Riemann zeta function beyond the region of convergence. The Zeta function's functional equation, linking its values at s and 1-s, is critical for studying the distribution of prime numbers and has profound implications in number theory and complex analysis.
Connections with Modular Forms
The Theta function plays a central role in the theory of modular forms by serving as a modular form itself or as a building block for constructing modular forms through its transformation properties under the modular group. The Zeta function, particularly the Riemann zeta function, connects to modular forms via the theory of L-functions and automorphic forms, where special values and functional equations reveal deep arithmetic information. Both functions exhibit symmetry and transformation behavior that underpin the structure of modular forms, linking number theory, complex analysis, and arithmetic geometry.
Role in Mathematical Physics
Theta functions play a crucial role in mathematical physics by characterizing heat distribution and quantum states on lattices, closely linked to modular forms and elliptic curves. Zeta functions, particularly the Riemann zeta function, are fundamental in spectral theory and quantum chaos, encoding the distribution of energy levels and exemplifying deep connections between number theory and physical phenomena. Both functions contribute to understanding partition functions and automorphic forms in statistical mechanics and string theory.
Computational Aspects and Algorithms
Theta functions and Zeta functions play crucial roles in computational number theory, with distinct algorithms tailored for their efficient evaluation. Fast Fourier Transform (FFT)-based methods accelerate the computation of Theta functions by exploiting their periodicity and modular transformations, enabling rapid series truncation. In contrast, Zeta function calculations leverage Euler-Maclaurin summation and Riemann-Siegel formulas, optimized for high-precision evaluation of critical line zeros and complex arguments.
Comparative Summary: Theta Function vs Zeta Function
The Theta function primarily encodes information about lattice points and has strong applications in number theory and mathematical physics, while the Zeta function, especially the Riemann Zeta, is pivotal in understanding the distribution of prime numbers through its complex analytic properties. Theta functions often exhibit modular transformation properties significant in topology and string theory, contrasting with the Zeta function's role in analytic continuation and the critical line hypothesis. Both functions share deep connections in analytic number theory but differ fundamentally in their domains and core applications, with Theta functions emphasizing periodicity and Zeta functions focusing on spectral and prime counting functions.
Theta function Infographic
 libterm.com
libterm.com