Cutting plane methods are essential in optimization for solving integer and combinatorial problems by iteratively refining feasible regions. These techniques enhance solution accuracy by systematically eliminating infeasible solutions without excluding any potential optimal points. Explore the rest of the article to understand how cutting planes can optimize your problem-solving strategies.
Table of Comparison
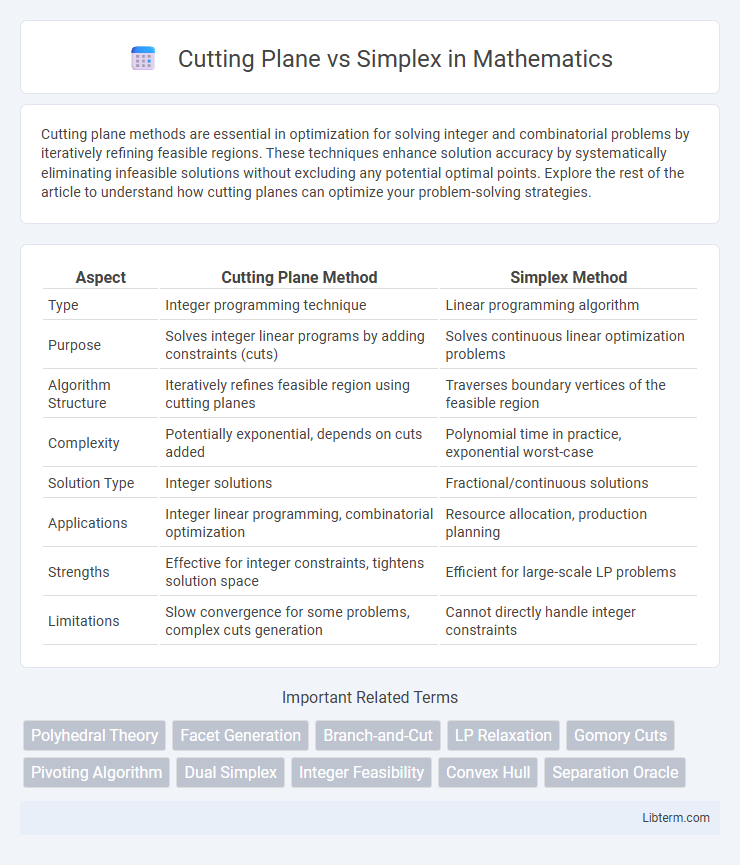
| Aspect | Cutting Plane Method | Simplex Method |
|---|---|---|
| Type | Integer programming technique | Linear programming algorithm |
| Purpose | Solves integer linear programs by adding constraints (cuts) | Solves continuous linear optimization problems |
| Algorithm Structure | Iteratively refines feasible region using cutting planes | Traverses boundary vertices of the feasible region |
| Complexity | Potentially exponential, depends on cuts added | Polynomial time in practice, exponential worst-case |
| Solution Type | Integer solutions | Fractional/continuous solutions |
| Applications | Integer linear programming, combinatorial optimization | Resource allocation, production planning |
| Strengths | Effective for integer constraints, tightens solution space | Efficient for large-scale LP problems |
| Limitations | Slow convergence for some problems, complex cuts generation | Cannot directly handle integer constraints |
Introduction to Linear Programming Methods
Linear programming methods, including Cutting Plane and Simplex algorithms, are fundamental for optimizing linear objective functions subject to constraints. The Simplex method iteratively moves along vertices of the feasible region to find the optimal solution, excelling in handling continuous variables efficiently. In contrast, the Cutting Plane method enhances feasibility by adding linear constraints that progressively eliminate fractional solutions in integer programming, making it vital for solving combinatorial optimization problems.
Overview of the Simplex Method
The Simplex method is a widely-used algorithm for solving linear programming problems by iteratively moving along the edges of the feasible region to find the optimal vertex. It efficiently handles constraints and objective functions by pivoting between basic feasible solutions, ensuring convergence to the optimal value for linear optimization. The method's strong theoretical foundation and practical performance make it a benchmark in operations research compared to alternative approaches like cutting plane methods.
Fundamentals of Cutting Plane Methods
Cutting plane methods iteratively refine feasible regions by adding linear constraints called cuts, which exclude non-integer solutions without removing any feasible integer points, enhancing integer programming solutions. Unlike the simplex algorithm that navigates vertices of the feasible polytope to optimize linear programs, cutting planes systematically tighten polyhedral approximations to approach integer optima. Central to cutting plane fundamentals is generating valid inequalities derived from problem structure or relaxation duality to progressively exclude fractional solutions in mixed-integer linear programming.
Key Differences: Cutting Plane vs Simplex
Cutting Plane and Simplex algorithms both solve linear programming problems but differ fundamentally in approach. The Simplex method iteratively moves along the edges of the feasible region to find optimal vertices, while the Cutting Plane method adds linear constraints to refine the feasible region and eliminate non-integer solutions in integer programming. Simplex is efficient for continuous variables, whereas Cutting Plane is specialized for integer and mixed-integer linear programming problems.
Advantages of the Simplex Method
The Simplex method offers significant advantages in solving large-scale linear programming problems efficiently, utilizing a systematic edge-following approach on the feasible region's vertices. It provides clear geometric interpretation and strong convergence guarantees in practice, often outperforming alternative algorithms like Cutting Plane in speed and computational resource utilization. The method's flexibility in handling degenerate vertices and its well-established pivot rules contribute to its widespread adoption in optimization, making it highly effective for diverse industrial applications.
Strengths of Cutting Plane Algorithms
Cutting plane algorithms excel in solving large-scale integer programming problems by iteratively refining the feasible region through the addition of linear inequalities, resulting in tighter relaxations compared to simplex methods. These algorithms effectively handle combinatorial optimization tasks by eliminating fractional solutions and improving convergence to integral optima. Their strength lies in systematically strengthening polyhedral approximations, which enhances solution accuracy for mixed-integer linear programs beyond the scope of traditional simplex techniques.
Computational Complexity Comparison
Cutting Plane and Simplex methods differ significantly in computational complexity, with Simplex often exhibiting exponential worst-case time despite typically performing efficiently in practice. Cutting Plane algorithms, based on iterative refinement via constraints, tend to have polynomial-time guarantees under specific problem structures but can be slower for large-scale linear programs due to the overhead of generating cuts. Empirical studies indicate that for high-dimensional and sparse problems, Simplex variants like Revised Simplex outperform classic Cutting Plane methods in runtime, although Cutting Plane remains competitive in integer programming contexts.
Practical Applications and Use Cases
Cutting Plane methods excel in integer programming problems commonly found in supply chain optimization and production scheduling, where discrete decision variables are crucial. The Simplex algorithm remains highly effective for continuous linear programming tasks such as portfolio optimization, resource allocation, and network flow models. Hybrid approaches integrating Cutting Plane and Simplex techniques are frequently employed in large-scale mixed-integer linear programming (MILP) problems within telecommunications and energy systems to enhance computational efficiency and solution accuracy.
Limitations and Challenges
Cutting Plane methods face challenges in scalability and may struggle with convergence on large-scale or highly non-convex integer programming problems due to the exponential growth of cutting planes and numerical instability. The Simplex algorithm, while efficient for linear programming, encounters limitations in integer and combinatorial optimization without modifications, often requiring branch-and-bound or branch-and-cut frameworks to handle discrete constraints. Both methods demand significant computational resources, and their performance heavily depends on problem structure, limiting applicability in real-time or highly complex optimization tasks.
Choosing the Right Method for Your Problem
Cutting Plane methods excel in large-scale integer programming problems due to their ability to iteratively refine feasible regions, while Simplex algorithms are highly efficient for linear programming with continuous variables. Selecting the right optimization technique depends on problem structure, size, and the presence of integer constraints; Simplex is preferable for smooth, linear models without integrality, whereas Cutting Plane is suited for combinatorial problems requiring integer solutions. Evaluating problem dimensionality and constraint complexity guides the choice between the speed of Simplex and the precision of Cutting Plane methods.
Cutting Plane Infographic
 libterm.com
libterm.com