An associated bundle is a construction in differential geometry that combines a principal bundle with a group representation to form a new fiber bundle. This concept allows the transformation of the structure group action into a more general setting, facilitating the study of vector bundles and fiber spaces linked to the principal bundle. Explore the rest of the article to understand how associated bundles serve as a powerful tool in geometrical and physical applications.
Table of Comparison
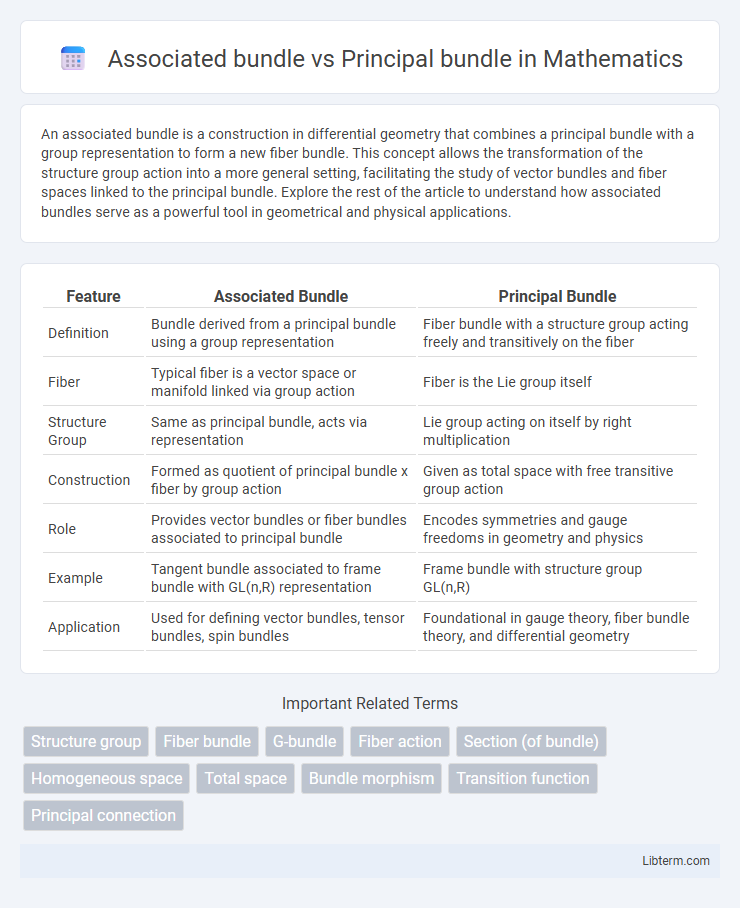
| Feature | Associated Bundle | Principal Bundle |
|---|---|---|
| Definition | Bundle derived from a principal bundle using a group representation | Fiber bundle with a structure group acting freely and transitively on the fiber |
| Fiber | Typical fiber is a vector space or manifold linked via group action | Fiber is the Lie group itself |
| Structure Group | Same as principal bundle, acts via representation | Lie group acting on itself by right multiplication |
| Construction | Formed as quotient of principal bundle x fiber by group action | Given as total space with free transitive group action |
| Role | Provides vector bundles or fiber bundles associated to principal bundle | Encodes symmetries and gauge freedoms in geometry and physics |
| Example | Tangent bundle associated to frame bundle with GL(n,R) representation | Frame bundle with structure group GL(n,R) |
| Application | Used for defining vector bundles, tensor bundles, spin bundles | Foundational in gauge theory, fiber bundle theory, and differential geometry |
Introduction to Fiber Bundles
Fiber bundles consist of a total space, base space, fiber, and projection map, with principal bundles having a structure group acting freely and transitively on the fiber, forming the framework for gauge theories. Associated bundles are constructed from principal bundles by using a representation of the structure group to define fibers that transform accordingly. Understanding the relationship between these bundles is fundamental in differential geometry and theoretical physics, enabling the study of vector bundles, connections, and gauge fields.
Defining Principal Bundles
Principal bundles are fiber bundles characterized by a continuous right action of a Lie group G acting freely and transitively on the fibers, ensuring each fiber is a G-torsor. They serve as the foundational structure from which associated bundles are constructed by attaching a typical fiber through a representation of G. The defining feature of principal bundles lies in their ability to encode geometric and topological information via their principal G-action and local trivializations respecting group structure.
Understanding Associated Bundles
Associated bundles are constructed from a principal G-bundle by replacing the fiber with a space on which G acts, creating a fiber bundle linked to the original principal bundle structure. Understanding associated bundles requires grasping how the group action on the fiber space induces a fiber bundle whose transition functions are determined by the principal bundle's transition functions. This relationship enables the translation of geometric or physical properties encoded in principal bundles into more general vector or fiber bundles.
Key Differences Between Principal and Associated Bundles
A principal bundle features a structure group acting freely and transitively on the fiber, allowing a global symmetry description, while an associated bundle is constructed from a principal bundle by attaching a typical fiber via a group representation. The principal bundle encodes the symmetry through its G-bundle structure, whereas the associated bundle translates this symmetry into a fiber space modeled on a vector space or manifold. Key differences include the principal bundle's role in defining connections and gauge transformations versus the associated bundle's function in representing fields or geometric objects induced by the principal bundle.
Structure Groups and Fiber Actions
Principal bundles feature a structure group that acts freely and transitively on the fiber, making the fiber isomorphic to the group itself. Associated bundles arise from a principal bundle by replacing the fiber with a space on which the structure group acts, inducing a fiber action consistent with the original principal bundle's group action. The transition from principal to associated bundles leverages the same structure group but modifies the fiber's nature through a specified group representation or action to create varied geometric or topological structures.
Construction of Associated Bundles from Principal Bundles
Associated bundles are constructed from principal bundles by replacing the typical fiber of the principal bundle with a space on which the structure group acts. Given a principal \( G \)-bundle \( P \) over a base space \( M \) and a left \( G \)-space \( F \), the associated bundle is formed as the quotient \( P \times_G F = (P \times F)/G \), where \( G \) acts diagonally on \( P \times F \). This construction preserves the fiber bundle structure and allows transferring the group action from the principal bundle to new fiber spaces, enabling applications in gauge theory and differential geometry.
Real-world Applications of Both Bundle Types
Associated bundles and principal bundles play critical roles in diverse real-world applications across physics and engineering. Principal bundles underpin gauge theories in particle physics, enabling the mathematical formalism for fields and forces through symmetry groups, while associated bundles represent matter fields as vector bundles linked to these principal bundles. In robotics and control systems, principal bundles model configuration spaces with symmetry, and associated bundles describe sensor and actuator data structured by group actions, facilitating coordinate-independent system analysis.
Isomorphisms and Morphisms in Bundle Theory
Isomorphisms between principal bundles are equivariant diffeomorphisms that respect the right action of the structure group, preserving the bundle's geometric structure. Morphisms of associated bundles arise from principal bundle morphisms combined with representations of the structure group, inducing equivariant maps between fibers. The classification of these morphisms and isomorphisms hinges on the interplay between bundle maps and group homomorphisms, reflecting the fundamental role of equivariance in bundle theory.
Topological and Geometric Properties
Associated bundles inherit their topological structure from principal bundles through the fiber product construction, preserving local triviality while allowing fiber types to vary according to a representation of the structure group. Principal bundles feature a free and transitive action of a Lie group on the fibers, ensuring a uniform geometric structure crucial for defining connections and curvature. The topology of principal bundles encodes transition functions that determine how associated bundles' fibers transform, linking their geometric properties through the bundle's group action and facilitating the study of gauge fields and fiberwise transformations.
Summary and Further Reading
An associated bundle is constructed from a principal bundle by attaching a typical fiber via a representation of the principal bundle's structure group, providing a way to translate principal bundle data into fiber bundles with additional structure. Principal bundles serve as the foundational objects in the theory of fiber bundles, characterized by a continuous free action of a Lie group that allows for the definition of connections and gauge transformations. For a deeper understanding, explore foundational texts like "Foundations of Differential Geometry" by Kobayashi and Nomizu and research articles on gauge theory and fiber bundle classifications.
Associated bundle Infographic
 libterm.com
libterm.com