Inverse limit is a powerful concept in topology and algebra that assembles a sequence of objects connected by morphisms into a single limiting object, capturing their consistent behavior. This construction finds applications in various fields such as dynamical systems, number theory, and category theory, providing a bridge between discrete structures and continuous ones. Explore the rest of this article to understand how inverse limits can deepen Your mathematical toolkit.
Table of Comparison
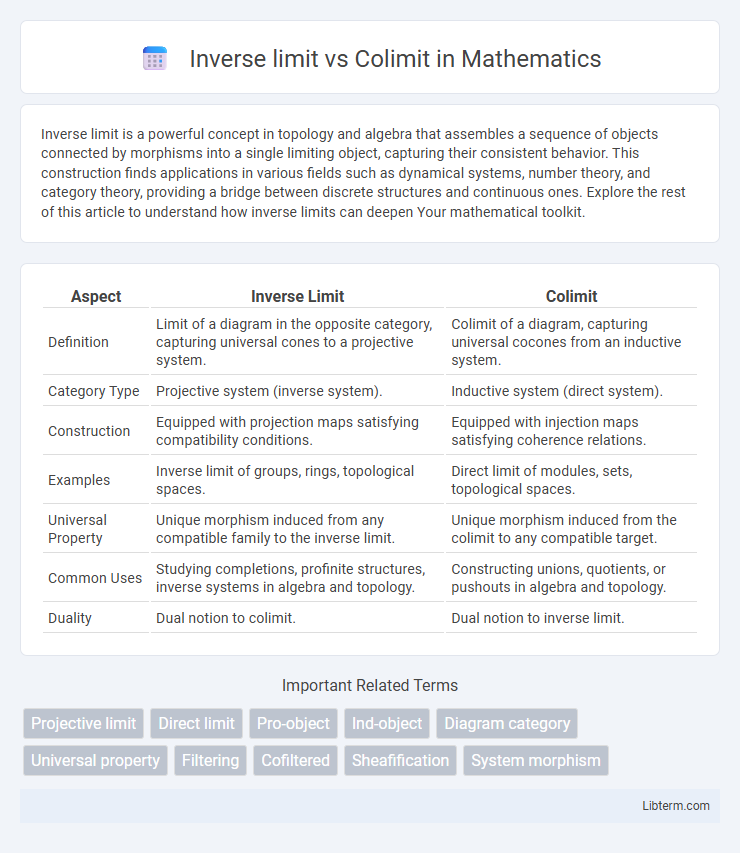
| Aspect | Inverse Limit | Colimit |
|---|---|---|
| Definition | Limit of a diagram in the opposite category, capturing universal cones to a projective system. | Colimit of a diagram, capturing universal cocones from an inductive system. |
| Category Type | Projective system (inverse system). | Inductive system (direct system). |
| Construction | Equipped with projection maps satisfying compatibility conditions. | Equipped with injection maps satisfying coherence relations. |
| Examples | Inverse limit of groups, rings, topological spaces. | Direct limit of modules, sets, topological spaces. |
| Universal Property | Unique morphism induced from any compatible family to the inverse limit. | Unique morphism induced from the colimit to any compatible target. |
| Common Uses | Studying completions, profinite structures, inverse systems in algebra and topology. | Constructing unions, quotients, or pushouts in algebra and topology. |
| Duality | Dual notion to colimit. | Dual notion to inverse limit. |
Introduction to Inverse Limits and Colimits
Inverse limits capture projective systems by linking objects through compatible morphisms, enabling the reconstruction of a limiting object reflecting the entire system's structure. Colimits, conversely, unify inductive systems by coalescing objects along morphisms into a single universal target, summarizing their combined properties. Both concepts serve as fundamental tools in category theory for analyzing and synthesizing mathematical structures through their respective universal constructions.
Fundamental Definitions
Inverse limits capture the notion of universal cones to a diagram indexed by a directed poset, representing a projective system's limit by systematically pulling structures back along morphisms. Colimits, dually, represent universal co-cones and describe inductive systems' limits by coherently pushing structures forward along morphisms. Both inverse limits and colimits serve as fundamental constructions in category theory, expressing how objects can be consistently assembled or decomposed across diagrams via universal properties.
Categorical Context: Limits and Colimits
Inverse limits and colimits serve as fundamental constructions in category theory, capturing universal properties related to diagrams of objects and morphisms. An inverse limit (or projective limit) represents a universal cone over a diagram, aggregating information through a limiting object that maps consistently to all objects in the diagram. Conversely, a colimit (or inductive limit) forms a universal co-cone, coherently amalgamating objects and morphisms into a single target object that reflects the diagram's structure.
Visualizing Inverse Limits vs Colimits
Visualizing inverse limits involves understanding a system of spaces or structures with compatible projection maps converging to a limiting object capturing consistent elements across the system. Colimits are visualized by assembling a directed diagram of spaces or objects along inclusion or morphism maps, merging them into a universal space that coherently unites all components. The key difference lies in inverse limits focusing on intersection and compatibility conditions, while colimits emphasize union and identification of components within the diagram.
Examples in Algebra: Groups and Modules
Inverse limits in algebra often appear as projective limits of groups or modules, such as the p-adic integers formed as the inverse limit of the system \(\mathbb{Z}/p^n\mathbb{Z}\). Colimits, by contrast, include direct limits like the direct union of increasing chain of subgroups or modules, exemplified by the direct limit of torsion groups forming the Prufer p-group. These constructions highlight dual universal properties: inverse limits capture compatible families of morphisms, while colimits aggregate objects through compatible identifications in categories of groups and modules.
Topological Applications of Inverse Limits and Colimits
Inverse limits capture the construction of spaces through inverse systems, enabling the analysis of fractals, continua, and shape theory in topology by preserving compactness and connectedness properties. Colimits assemble spaces via direct systems, facilitating the formation of quotients, pushouts, and cell complexes, which are crucial in homotopy theory and CW-complex construction. Both inverse limits and colimits provide fundamental tools for understanding topological structures, with inverse limits focusing on limiting processes of spaces and colimits enabling gluing and amalgamation.
Key Differences: Inverse Limit vs Colimit
Inverse limits construct objects representing compatible tuples from a directed system of inverse morphisms, capturing universal properties as limits in category theory. Colimits, conversely, assemble objects by identifying and coalescing data across a directed system of morphisms, serving as universal constructions for co-cones. Key differences lie in their directional approach: inverse limits use projective systems with morphisms pointing backward, while colimits employ inductive systems with morphisms pointing forward, reflecting dual notions in categorical frameworks.
Functorial Properties and Universal Constructions
Inverse limits and colimits represent dual universal constructions in category theory, characterized by their opposite variance regarding diagrams and cones. Inverse limits arise as terminal objects in the category of cones over a diagram, exhibiting contravariant functoriality that preserves limits through limit-preserving functors. Colimits, conversely, serve as initial objects in the cocone category, displaying covariant functorial properties that ensure colimit preservation under colimit-preserving functors, reflecting their fundamental role in constructing objects via universal properties.
Common Pitfalls and Misunderstandings
Inverse limits and colimits often cause confusion due to their dual nature in category theory, where inverse limits capture projective limits over diagrams directed by morphisms going backward, while colimits represent inductive limits with morphisms going forward. Common pitfalls include assuming all limits and colimits exist in a given category, neglecting the difference between inverse limits preserving limits but not always colimits, and ignoring how inverse limits can fail to preserve exact sequences in homological algebra. Misunderstandings also arise from conflating pointwise limits in functor categories with categorical limits, as well as overlooking size and completeness conditions required for both inverse limits and colimits to exist and behave as expected.
Conclusion: Choosing Between Inverse Limit and Colimit
Choosing between inverse limits and colimits depends on the directionality and nature of the diagram in category theory, with inverse limits handling projective systems and colimits addressing inductive systems. Inverse limits capture universal properties related to limiting objects under compatible morphisms, while colimits aggregate objects via co-cones reflecting colimiting behavior. Understanding these distinctions is crucial for selecting the appropriate construction in algebraic topology, homological algebra, or related mathematical frameworks.
Inverse limit Infographic
 libterm.com
libterm.com