A monoidal category is a category equipped with a tensor product, an identity object, and natural isomorphisms that satisfy specific coherence conditions, enabling the formalization of processes that combine objects and morphisms. This structure is foundational in areas like category theory, quantum computing, and algebra, providing a framework for understanding parallel composition and interaction. Explore this article further to uncover how monoidal categories shape modern mathematical and computational theories.
Table of Comparison
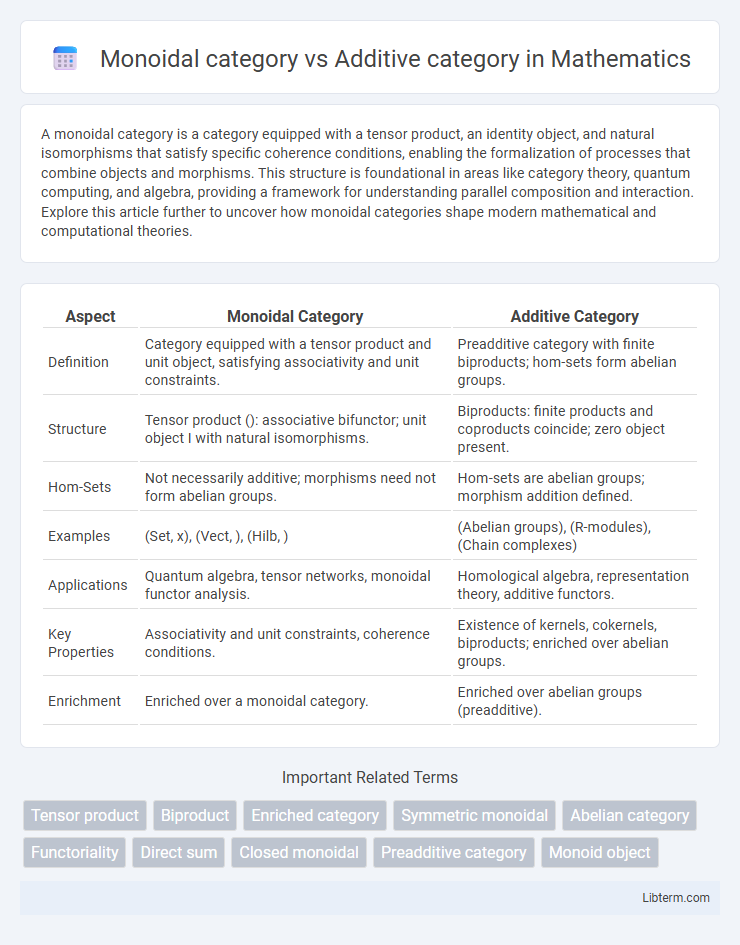
| Aspect | Monoidal Category | Additive Category |
|---|---|---|
| Definition | Category equipped with a tensor product and unit object, satisfying associativity and unit constraints. | Preadditive category with finite biproducts; hom-sets form abelian groups. |
| Structure | Tensor product (): associative bifunctor; unit object I with natural isomorphisms. | Biproducts: finite products and coproducts coincide; zero object present. |
| Hom-Sets | Not necessarily additive; morphisms need not form abelian groups. | Hom-sets are abelian groups; morphism addition defined. |
| Examples | (Set, x), (Vect, ), (Hilb, ) | (Abelian groups), (R-modules), (Chain complexes) |
| Applications | Quantum algebra, tensor networks, monoidal functor analysis. | Homological algebra, representation theory, additive functors. |
| Key Properties | Associativity and unit constraints, coherence conditions. | Existence of kernels, cokernels, biproducts; enriched over abelian groups. |
| Enrichment | Enriched over a monoidal category. | Enriched over abelian groups (preadditive). |
Introduction to Monoidal and Additive Categories
Monoidal categories provide a framework where objects are equipped with a tensor product, enabling the composition of objects and morphisms with associativity and unit constraints, fundamental in fields like algebra and quantum mechanics. Additive categories extend this structure by incorporating biproducts, where morphism sets form abelian groups and every finite set of objects has a direct sum, crucial for homological algebra and representation theory. Understanding the distinction highlights that while all additive categories can be seen as enriched over abelian groups, monoidal categories focus on tensorial composition without requiring an additive structure.
Fundamental Definitions and Concepts
A monoidal category is defined by a tensor product operation that combines objects and morphisms, equipped with an associative constraint and a unit object satisfying coherence conditions. An additive category, on the other hand, is characterized by having biproducts, where morphism sets form abelian groups and composition is bilinear. While monoidal categories emphasize the tensor structure and associativity, additive categories focus on additive structures and direct sum decompositions within their morphism sets.
Core Structures: Tensor Products vs Direct Sums
Monoidal categories are defined by core structures centered around tensor products, which provide a bifunctor that combines objects and morphisms adhering to associativity and unit constraints, enabling the modeling of multiplicative interactions. In contrast, additive categories emphasize direct sums as fundamental constructions, offering biproducts that serve as both products and coproducts, facilitating linear algebraic operations and decompositions. While tensor products in monoidal categories capture the concept of parallel composition, direct sums in additive categories represent explicit additive combination, highlighting distinct algebraic paradigms within category theory.
Morphisms in Monoidal and Additive Categories
Morphisms in a monoidal category preserve the tensor product structure, satisfying coherence conditions such as compatibility with associativity and unit constraints, enabling composition that respects the monoidal operation. In an additive category, morphisms form abelian groups and the composition of morphisms is bilinear, allowing for the addition and zero morphism, which reflects the additive structure of objects. The interaction of morphisms in monoidal categories emphasizes tensorial composition, whereas in additive categories, the focus lies on morphism addition and group-theoretic properties.
Units and Neutral Objects: Comparison
In a monoidal category, the unit object serves as the neutral element for the tensor product, satisfying the coherence conditions given by natural isomorphisms known as the left and right unit laws. An additive category, on the other hand, possesses a zero object that acts as both initial and terminal, functioning as the neutral element for the biproduct operation. While the monoidal unit object ensures associativity and unity under the tensor product, the zero object in additive categories guarantees the existence of additive identities and morphisms nullifying compositions.
Enriched Categories and Their Roles
Monoidal categories provide a framework for enrichment by equipping a category with a tensor product and unit object, enabling the definition of enriched categories where hom-sets inherit additional structure from the monoidal base. Additive categories, characterized by having biproducts and abelian group structures on hom-sets, serve as natural enrichment bases for categories enriched over abelian groups, facilitating the study of modules and homological algebra. The interplay between monoidal and additive categories in enriched category theory allows for robust generalizations of limits, colimits, and morphisms, enhancing the analysis of categorical structures in algebra and topology.
Examples of Monoidal vs Additive Categories
Monoidal categories include examples such as the category of vector spaces with the tensor product and the category of sets with the Cartesian product, emphasizing a bifunctorial operation that is associative up to isomorphism. Additive categories, by contrast, feature examples like the category of abelian groups or modules over a ring, where hom-sets are endowed with abelian group structures and where biproducts serve as both products and coproducts. While monoidal categories generalize tensor-like structures, additive categories focus on enriching morphisms with additive structure and enforcing direct sum decompositions.
Applications in Mathematics and Physics
Monoidal categories provide a foundational framework for tensor products and dualities, crucial in quantum physics, topological quantum field theory, and representation theory, enabling the modeling of particle interactions and quantum entanglement. Additive categories, characterized by direct sums and zero morphisms, are essential in homological algebra and algebraic geometry, facilitating the study of exact sequences and derived functors. Both structures underpin advanced mathematical physics, with monoidal categories shaping categorical quantum mechanics and additive categories supporting cohomological methods in string theory.
Similarities and Key Differences
Monoidal categories and additive categories both provide frameworks for combining objects and morphisms, with monoidal categories emphasizing a tensor product operation and additive categories focusing on direct sums and zero morphisms. Both structures exhibit associativity and unit elements, but monoidal categories rely on coherence conditions for the tensor product, whereas additive categories require abelian group structures on hom-sets. Key differences include the monoidal category's general notion of multiplication versus the additive category's emphasis on additive structure and biproducts.
Conclusion and Future Perspectives
Monoidal categories provide a foundational framework for tensor product structures, while additive categories emphasize the direct sum operations essential in homological algebra. Future research is expected to explore enriched categorical structures that unify these concepts, enhancing computational techniques in representation theory and quantum algebra. Advances in higher category theory may further integrate monoidal and additive properties, fostering new applications in mathematical physics and category theory.
Monoidal category Infographic
 libterm.com
libterm.com