Crystalline cohomology provides a powerful tool for studying algebraic varieties over fields of positive characteristic, capturing intricate geometric and arithmetic properties through p-adic methods. It serves as a bridge between algebraic geometry and number theory by offering insights that are not accessible via classical cohomology theories. Discover how crystalline cohomology can deepen your understanding of modern algebraic structures by exploring the detailed concepts in the rest of this article.
Table of Comparison
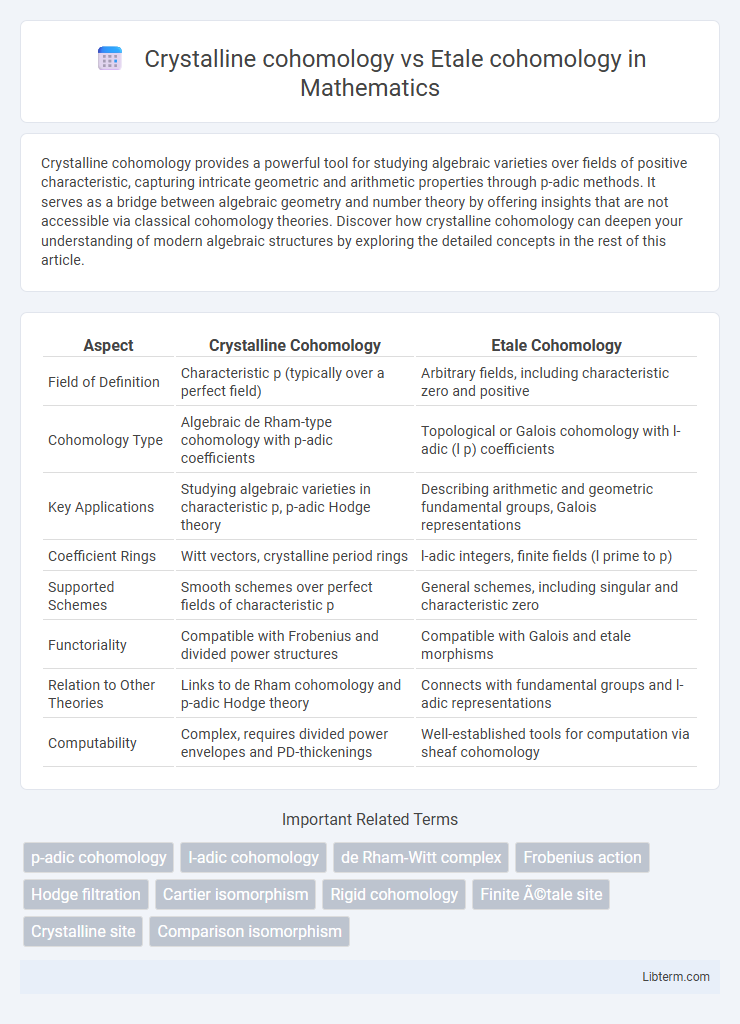
| Aspect | Crystalline Cohomology | Etale Cohomology |
|---|---|---|
| Field of Definition | Characteristic p (typically over a perfect field) | Arbitrary fields, including characteristic zero and positive |
| Cohomology Type | Algebraic de Rham-type cohomology with p-adic coefficients | Topological or Galois cohomology with l-adic (l p) coefficients |
| Key Applications | Studying algebraic varieties in characteristic p, p-adic Hodge theory | Describing arithmetic and geometric fundamental groups, Galois representations |
| Coefficient Rings | Witt vectors, crystalline period rings | l-adic integers, finite fields (l prime to p) |
| Supported Schemes | Smooth schemes over perfect fields of characteristic p | General schemes, including singular and characteristic zero |
| Functoriality | Compatible with Frobenius and divided power structures | Compatible with Galois and etale morphisms |
| Relation to Other Theories | Links to de Rham cohomology and p-adic Hodge theory | Connects with fundamental groups and l-adic representations |
| Computability | Complex, requires divided power envelopes and PD-thickenings | Well-established tools for computation via sheaf cohomology |
Introduction to Cohomology Theories
Crystalline cohomology provides a powerful tool for studying algebraic varieties over fields of positive characteristic by capturing p-adic information through infinitesimal thickenings, whereas Etale cohomology uses the notion of covering spaces to analyze the topology of varieties in a way compatible with Galois actions. Both theories serve as fundamental frameworks within algebraic geometry, linking geometric properties to arithmetic and topological invariants. Understanding their contrasting approaches--crystalline's focus on deformation and infinitesimal structures versus etale's reliance on topological and Galois-theoretic methods--is essential for deep insights into the cohomological behavior of schemes in various geometric and arithmetic contexts.
Overview of Étale Cohomology
Etale cohomology is a powerful tool in algebraic geometry used to study the topological properties of algebraic varieties over fields with positive characteristic by employing Grothendieck topologies. It provides important invariants, such as l-adic cohomology groups, which are crucial for understanding the arithmetic and geometric structure of varieties, especially in contexts where classical cohomology theories fail. Compared to crystalline cohomology, which deals with p-adic coefficients and infinitesimal neighborhoods, etale cohomology allows for the analysis of the fundamental group and Galois representations, making it essential for applications like the proof of the Weil conjectures.
Overview of Crystalline Cohomology
Crystalline cohomology is a p-adic cohomology theory designed for algebraic varieties over fields of positive characteristic, providing a powerful tool to study their arithmetic and geometric properties. It captures infinitesimal deformation data through crystals on the crystalline site, linking the de Rham cohomology in characteristic zero with etale cohomology in characteristic p. Unlike etale cohomology, which uses the etale topology and Galois representations, crystalline cohomology exploits the structure of the Witt vectors and divided power thickenings to compute p-adic invariants and understand the arithmetic of schemes in characteristic p.
Historical Context and Motivation
Crystalline cohomology, developed by Alexander Grothendieck and Pierre Berthelot in the 1960s and 1970s, aimed to provide a cohomology theory for algebraic varieties in characteristic p that parallels de Rham cohomology in characteristic zero. Etale cohomology, introduced earlier by Grothendieck in the 1960s, was motivated by the need for a cohomological tool to tackle problems in arithmetic geometry, particularly those involving the Weil conjectures. Both theories emerged as key frameworks for understanding the structure of varieties over fields of positive characteristic, with crystalline cohomology addressing limitations of etale cohomology in p-adic contexts.
Fundamental Differences in Construction
Crystalline cohomology is constructed using a sheaf of differential forms on the crystalline site, which is defined over a scheme in characteristic p and incorporates infinitesimal thickenings, while etale cohomology is built from the etale topology using inverse limits of sheaves of abelian groups and focuses on covering spaces with respect to the etale morphisms. Crystalline cohomology captures p-adic and infinitesimal deformation information through its use of divided power structures, whereas etale cohomology provides a tool to study algebraic varieties via Galois actions and topological analogs through its emphasis on etale covers. The fundamental difference lies in crystalline cohomology's reliance on a richer infinitesimal structure suited for characteristic p and deformation theory, contrasting with etale cohomology's use of a topological-like approach applicable across different characteristics.
Applications in Arithmetic Geometry
Crystalline cohomology provides powerful tools for studying algebraic varieties in characteristic p, enabling effective analysis of p-adic Hodge theory and deformation problems in arithmetic geometry. Etale cohomology excels in capturing information about the fundamental group and Galois actions on varieties over fields of arbitrary characteristic, facilitating proofs of major results like the Weil conjectures and modularity theorems. Both cohomology theories are essential for investigating arithmetic schemes, with crystalline cohomology focusing on infinitesimal structures and etale cohomology addressing topological and arithmetic properties.
Comparison in Characteristic p Settings
Crystalline cohomology and etale cohomology both serve as powerful tools for studying algebraic varieties over fields of characteristic p, with crystalline cohomology providing a p-adic, deformation-theoretic approach that captures infinitesimal structure via divided power thickenings. Etale cohomology, in contrast, offers a topological perspective defined through the etale topology, enabling the use of Galois representations and l-adic coefficients (with l p) to avoid inseparability issues inherent in characteristic p. While etale cohomology excels in encoding arithmetic information and has strong links to the fundamental group, crystalline cohomology is better suited for understanding p-adic Hodge theory and integral structures, often complementing etale cohomology particularly through comparison theorems in p-adic Hodge theory contexts.
Key Theorems and Results Linking Both
Crystalline cohomology and Etale cohomology are connected through the comparison theorems established by Berthelot and Ogus, which provide isomorphisms between crystalline cohomology and p-adic etale cohomology under certain conditions. The Hyodo-Kato theorem links log-crystalline cohomology with p-adic etale cohomology for varieties with semistable reduction, while the Fontaine-Messing theory gives a bridge between crystalline cohomology and Galois representations in p-adic Hodge theory. These key results allow the transfer of geometric information in characteristic p settings to arithmetic properties apparent in the etale cohomology framework.
Strengths and Limitations of Each Theory
Crystalline cohomology excels in providing integral p-adic cohomological invariants for schemes in characteristic p, capturing fine arithmetic information especially for smooth and proper varieties; however, it is limited by its complexity and difficulty in handling singular or non-proper schemes. Etale cohomology offers a flexible and powerful tool for defining Galois representations and working with torsion coefficients across a broad class of varieties, including those not of characteristic p, but it lacks integral p-adic structures and may fail to capture certain finer arithmetic properties. Both theories complement each other, with crystalline cohomology focusing on p-adic period rings and Frobenius actions, while etale cohomology provides accessible connections to fundamental groups and l-adic representations.
Future Directions and Open Problems
Future directions in crystalline cohomology focus on refining p-adic Hodge theory applications and enhancing comparisons with etale cohomology in mixed characteristic settings. Open problems include understanding the integral structures within crystalline representations and extending the theory to broader classes of singular schemes. Developing computational tools to bridge crystalline and etale cohomology remains crucial for advancing arithmetic geometry and number theory.
Crystalline cohomology Infographic
 libterm.com
libterm.com