An open set is a fundamental concept in topology, characterized by containing none of its boundary points and allowing every point inside it to have a neighborhood fully contained within the set. Understanding open sets is essential for grasping more advanced topics like continuity, convergence, and compactness in mathematical analysis. Explore the rest of the article to deepen your knowledge about open sets and their crucial role in topology.
Table of Comparison
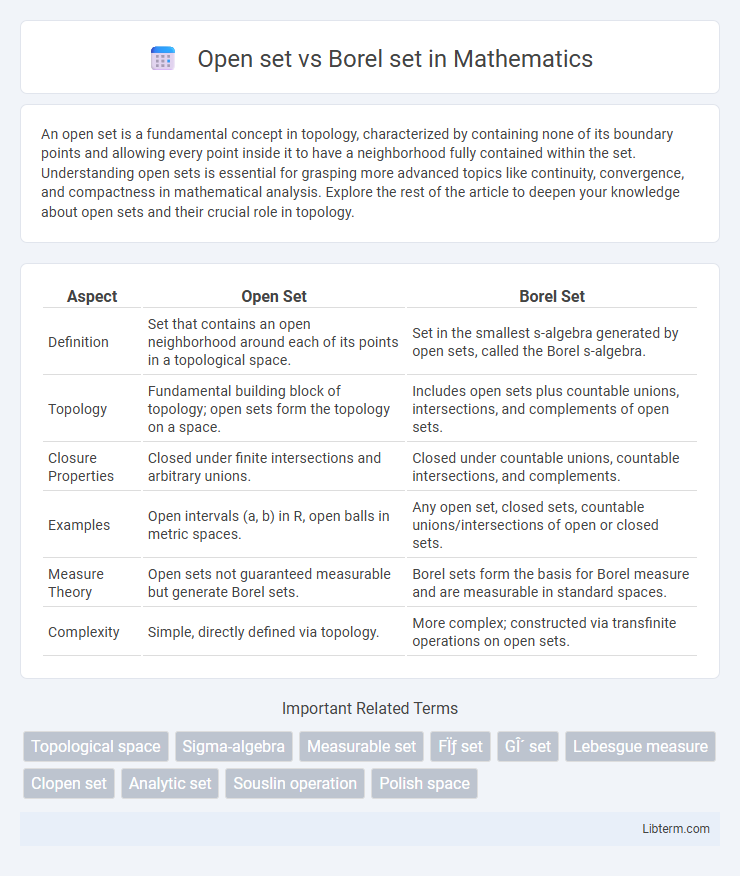
| Aspect | Open Set | Borel Set |
|---|---|---|
| Definition | Set that contains an open neighborhood around each of its points in a topological space. | Set in the smallest s-algebra generated by open sets, called the Borel s-algebra. |
| Topology | Fundamental building block of topology; open sets form the topology on a space. | Includes open sets plus countable unions, intersections, and complements of open sets. |
| Closure Properties | Closed under finite intersections and arbitrary unions. | Closed under countable unions, countable intersections, and complements. |
| Examples | Open intervals (a, b) in R, open balls in metric spaces. | Any open set, closed sets, countable unions/intersections of open or closed sets. |
| Measure Theory | Open sets not guaranteed measurable but generate Borel sets. | Borel sets form the basis for Borel measure and are measurable in standard spaces. |
| Complexity | Simple, directly defined via topology. | More complex; constructed via transfinite operations on open sets. |
Introduction to Set Theory Concepts
Open sets in topology refer to collections of points forming neighborhoods where each point has a surrounding region entirely contained within the set, essential for defining continuity and limits. Borel sets, generated from open sets through countable unions, intersections, and complements, form the Borel s-algebra crucial for measure theory and probability. Understanding these sets lays the foundation for advanced set theory, linking topological structures with measurable frameworks and enabling rigorous analysis in mathematics.
Defining Open Sets in Topology
Open sets in topology are defined as collections of points where each point has a neighborhood entirely contained within the set, forming the basis for topological spaces. Borel sets arise from the sigma-algebra generated by all open sets, including countable unions and intersections, which extend beyond open sets to encompass measurable structures. Understanding the distinction between open sets as foundational building blocks and Borel sets as measurable extensions is essential for deeper studies in topology and measure theory.
Understanding Borel Sets
Borel sets are generated from open sets through countable unions, intersections, and complements, forming the smallest s-algebra containing all open sets in a topological space. Understanding Borel sets is fundamental in measure theory because they provide the framework for defining Borel measures and enable rigorous integration and probability calculations. Their structure extends the concept of openness to include more complex measurable sets essential for descriptive set theory and real analysis.
Hierarchy of Borel Sets
The hierarchy of Borel sets is constructed through the transfinite iteration of operations starting from open sets, generating increasingly complex classes known as S^0_a and P^0_a sets for countable ordinals a. Open sets form the base level (S^0_1) of this hierarchy, while Borel sets encompass all sets obtainable via countable unions, intersections, and complements applied to open sets, resulting in a rich structure stratified by descriptive complexity. This classification captures the intricate relationships between open sets and higher-level Borel sets in measurable spaces, central to descriptive set theory and real analysis.
Key Properties of Open Sets
Open sets in topology are characterized by the property that every point within the set has a neighborhood entirely contained in the set, ensuring local openness and continuity. Unlike Borel sets, which are generated through countable unions, intersections, and complements of open sets, open sets are the fundamental building blocks of the Borel s-algebra. Key properties of open sets include closure under arbitrary unions and finite intersections, making them essential for defining topological spaces and continuous functions.
Generation of Borel Sets from Open Sets
Borel sets are generated from open sets through the process of countable operations including unions, intersections, and complements, forming the smallest sigma-algebra containing all open sets in a topological space. Open sets serve as the foundational elements in the Borel sigma-algebra, allowing the construction of complex measurable sets essential in measure theory and descriptive set theory. This generation process ensures that every Borel set can be approximated or described in terms of simpler open sets, facilitating analysis in real analysis and probability.
Differences Between Open and Borel Sets
Open sets form the foundation of a topology, characterized by containing none of their boundary points and serving as the building blocks for more complex sets. Borel sets are generated from open sets through countable unions, intersections, and complements, creating the smallest s-algebra containing all open sets. Unlike open sets, which are purely topological, Borel sets accommodate measurable structures essential for probability theory and real analysis.
Examples Illustrating Open and Borel Sets
Open sets in \(\mathbb{R}\) often include intervals such as \((0,1)\) or \((-\infty, 5)\), where every point has a neighborhood entirely contained within the set. Borel sets extend beyond open sets by including any set formed from countable unions, intersections, or complements of open sets, such as closed intervals like \([0,1]\) or the Cantor set. For instance, the interval \([0,1]\) is a Borel set but not an open set, while \((0,1)\) is both open and Borel, illustrating the hierarchy between these classes of sets.
Applications of Open and Borel Sets in Mathematics
Open sets are fundamental in topology, serving as the basis for defining continuous functions and convergence in metric spaces, thereby enabling rigorous analysis in calculus and functional analysis. Borel sets, generated from open sets through countable operations, are crucial in measure theory as they form the standard s-algebra on which Lebesgue measures are defined, facilitating integration and probability theory. Applications of these sets extend to descriptive set theory, ergodic theory, and stochastic processes, where the distinction between open and Borel sets underpins the study of measurability and topological structure.
Conclusion: Comparing Open and Borel Sets
Open sets form the fundamental building blocks of topology, defined by containing neighborhoods around each of their points, while Borel sets comprise the smallest s-algebra generated by open sets and include more complex constructions such as countable unions, intersections, and complements of open sets. The main distinction lies in their structural complexity: open sets are simpler and used to define continuity and convergence, whereas Borel sets enable rigorous measure theory and probability applications by encompassing a wider class of measurable sets. Understanding the relationship between open and Borel sets is essential for analyzing measurable spaces and developing advanced results in real analysis and mathematical probability.
Open set Infographic
 libterm.com
libterm.com