A Borel measure assigns a consistent size or volume to the Borel sets, which are the most comprehensive collection of sets generated from open or closed sets in a topological space. This concept serves as a fundamental tool in measure theory, enabling the integration and probability assessments on complex spaces. Explore the rest of this article to understand how Borel measures shape analysis in modern mathematics and your work in related fields.
Table of Comparison
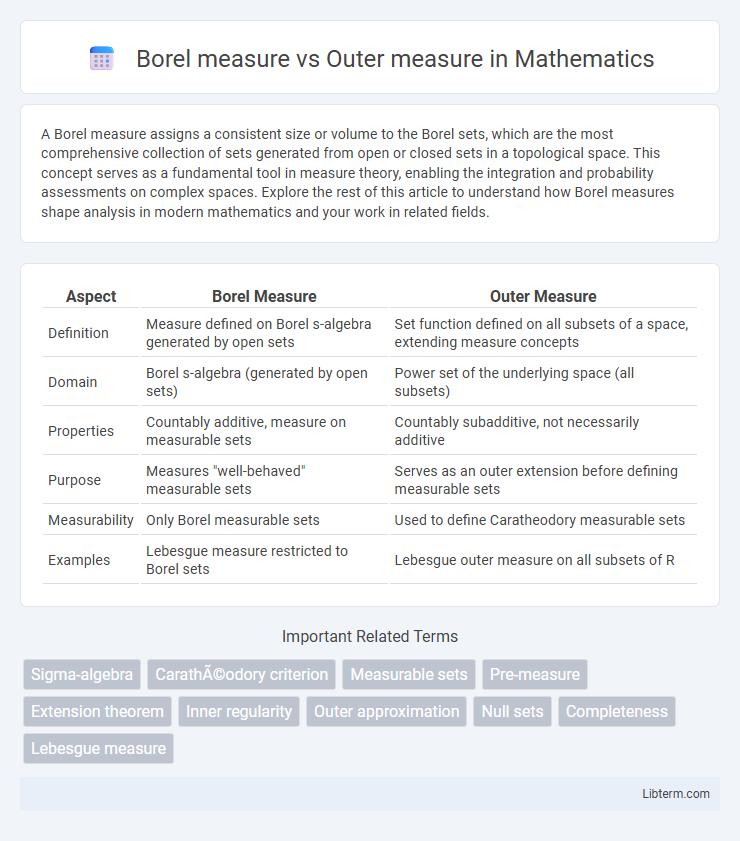
| Aspect | Borel Measure | Outer Measure |
|---|---|---|
| Definition | Measure defined on Borel s-algebra generated by open sets | Set function defined on all subsets of a space, extending measure concepts |
| Domain | Borel s-algebra (generated by open sets) | Power set of the underlying space (all subsets) |
| Properties | Countably additive, measure on measurable sets | Countably subadditive, not necessarily additive |
| Purpose | Measures "well-behaved" measurable sets | Serves as an outer extension before defining measurable sets |
| Measurability | Only Borel measurable sets | Used to define Caratheodory measurable sets |
| Examples | Lebesgue measure restricted to Borel sets | Lebesgue outer measure on all subsets of R |
Introduction to Measure Theory
Borel measure is defined on the s-algebra generated by open sets in a topological space, focusing on measurable subsets that align with the topology's structure. Outer measure extends the notion of measure to all subsets by assigning a value based on covering properties, serving as a foundational tool to construct measures like the Lebesgue measure. In measure theory, understanding the distinction between Borel measures and outer measures is critical for developing integration and probability frameworks on complex spaces.
Defining Borel Measures
Borel measures are defined on the s-algebra generated by open sets in a topological space, ensuring measurability of all Borel sets. These measures extend from simpler measures on open or closed sets and satisfy countable additivity, distinguishing them from outer measures, which are defined on all subsets but only require countable subadditivity. The construction of Borel measures often involves Caratheodory's extension theorem, which systematically extends pre-measures defined on algebraic structures to complete Borel measures.
Understanding Outer Measures
Outer measures generalize the concept of length or size to all subsets of a given set by assigning a non-negative extended real number that is countably subadditive and zero for the empty set. Unlike Borel measures, which are defined only on Borel sigma-algebras generated by open sets, outer measures provide a way to measure arbitrary sets before restricting to measurable sets that satisfy Caratheodory's criterion. The construction of an outer measure serves as a foundational step in measure theory, enabling the extension from simple measurable sets to a complete measure that aligns with intuitive notions of size.
Key Differences Between Borel and Outer Measures
Borel measures are defined on the sigma-algebra generated by open sets in a topological space, ensuring measurability of all Borel sets, whereas outer measures are defined on all subsets, providing a more general, pre-measure framework. Outer measures are characterized by countable subadditivity and monotonicity but may fail to be additive or fully measurable without further restriction. The essential difference lies in Borel measures guaranteeing countable additivity on a well-structured sigma-algebra, while outer measures serve as an extension tool for constructing measures on broader set collections.
Construction of Borel Measures
Borel measures arise from restricting outer measures to the Borel sigma-algebra generated by open sets, ensuring countable additivity over Borel sets. The construction typically begins with an outer measure defined on all subsets, such as the Lebesgue outer measure, which is then Caratheodory restricted to obtain a Borel measure. This process guarantees that Borel measures are regular and compatible with the topology of the underlying space, making them fundamental in real analysis and probability theory.
Construction of Outer Measures
The construction of outer measures begins with defining a function on all subsets of a given set that is countably subadditive, monotone, and assigns zero to the empty set, serving as an extension of pre-measures on sigma-algebras. Outer measures provide a foundational tool for measure theory by facilitating the Caratheodory construction, which identifies measurable sets, including Borel sets, through a criterion based on the measure of intersections and complements. Unlike Borel measures that are directly defined on Borel sigma-algebras generated by open sets, outer measures extend the concept to all subsets before restricting to measurable sets, ensuring complete and regular measures.
Measurable Sets in Borel vs Outer Measure
Borel measure is defined on Borel sets, which form the smallest sigma-algebra generated by open sets in a topological space, ensuring all Borel sets are measurable by definition. Outer measure extends beyond Borel sets, assigning measure to all subsets, but measurable sets with respect to an outer measure satisfy Caratheodory's criterion, allowing a broader class of sets including non-Borel measurable sets. The distinction lies in Borel measurability restricting to sigma-algebras generated by topology, whereas outer measure-induced measurability includes sets measurable under the outer measure extension, often leading to a larger sigma-algebra than the Borel sigma-algebra.
Applications of Borel Measures
Borel measures are essential in probability theory and functional analysis, providing a framework for integrating functions over topological spaces and constructing probability distributions on Borel sets. They facilitate the definition of measures on sigma-algebras generated by open or closed sets, enabling rigorous treatment of measurable spaces in real analysis and stochastic processes. In contrast, outer measures serve as preliminary tools for extending measures, but Borel measures allow direct application in areas such as ergodic theory, harmonic analysis, and measure-theoretic probability.
Applications of Outer Measures
Outer measures extend the concept of measure to a broader class of sets, enabling the construction of Lebesgue measure and facilitating measure theory in non-measurable contexts. They are fundamental in probability theory and fractal geometry for defining measures on irregular or complex sets where Borel measures may fail or be insufficient. Applications of outer measures include determining measurable envelopes, establishing Caratheodory measurability, and providing a foundation for integration on general metric spaces.
Summary: Choosing Between Borel and Outer Measures
Borel measures are defined on the s-algebra generated by open sets, making them suitable for well-structured spaces with topological properties, while outer measures provide a more general approach by assigning measures to all subsets, facilitating the extension of measures to larger classes. In applications requiring measurable sets with topological relevance, Borel measures offer more intuitive frameworks, whereas outer measures enable the construction of measures from pre-measures using Caratheodory's criterion. Selecting between Borel and outer measures depends on the need for topological structure versus generality and completeness in measure extension.
Borel measure Infographic
 libterm.com
libterm.com