Limit refers to the maximum boundary or point beyond which something cannot extend or continue, whether in physical, mathematical, or conceptual contexts. Understanding limits is crucial in various fields such as calculus, where it defines the behavior of functions, or in everyday life where boundaries help maintain order and safety. Explore the rest of the article to discover how limits influence different aspects of your world.
Table of Comparison
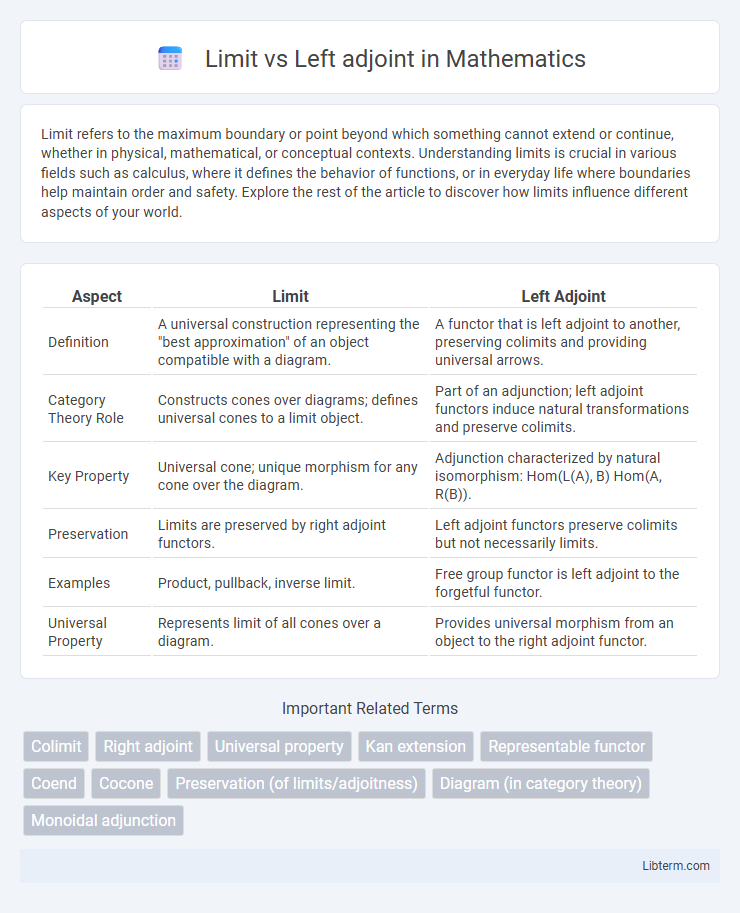
| Aspect | Limit | Left Adjoint |
|---|---|---|
| Definition | A universal construction representing the "best approximation" of an object compatible with a diagram. | A functor that is left adjoint to another, preserving colimits and providing universal arrows. |
| Category Theory Role | Constructs cones over diagrams; defines universal cones to a limit object. | Part of an adjunction; left adjoint functors induce natural transformations and preserve colimits. |
| Key Property | Universal cone; unique morphism for any cone over the diagram. | Adjunction characterized by natural isomorphism: Hom(L(A), B) Hom(A, R(B)). |
| Preservation | Limits are preserved by right adjoint functors. | Left adjoint functors preserve colimits but not necessarily limits. |
| Examples | Product, pullback, inverse limit. | Free group functor is left adjoint to the forgetful functor. |
| Universal Property | Represents limit of all cones over a diagram. | Provides universal morphism from an object to the right adjoint functor. |
Introduction to Limits and Left Adjoints
In category theory, a limit represents a universal cone that encapsulates the essence of a diagram, serving as a fundamental construction that generalizes products and pullbacks. Left adjoints, as functors, preserve colimits and correspond to the universal properties opposite to limits, establishing an essential relationship between adjoint functors and limits. Understanding limits involves comprehending their role in representing objects defined by universal mapping properties, while left adjoints provide a framework for constructing and characterizing these universal objects through categorical adjunctions.
Categorical Foundations: Functors and Morphisms
Limits in category theory capture universal cones to diagrams, representing consolidated structures preserving morphisms, while left adjoints serve as functors providing optimal approximations that preserve colimits and establish adjunctions with right adjoints. The interplay between limits and left adjoints underpins the foundational understanding of how functors interact with morphisms, where left adjoints uniquely mediate transformations respecting categorical limits. This duality reflects categorical constructions' essence, ensuring coherence in mapping structures across categories through universal properties intrinsic to functorial behavior.
Defining Limits in Category Theory
Limits in category theory generalize universal constructions by providing a canonical cone over a diagram that factors uniquely through any other cone, capturing notions like products and pullbacks. A left adjoint functor preserves all colimits, while right adjoints preserve all limits, establishing a fundamental relationship between adjointness and limit preservation. Defining limits involves identifying an object together with morphisms satisfying a universal property that uniquely factors cones from the diagram into the category.
Understanding Left Adjoints
Left adjoints are functors that preserve colimits and reflect universal properties, making them essential in category theory for constructing and analyzing objects from simpler components. They arise naturally as companions to right adjoints, which preserve limits, and their existence often guarantees the presence of free constructions or extensions. Understanding left adjoints involves studying their role in adjunctions, how they facilitate the transfer of structures, and their applications in areas such as algebra, topology, and logic.
Universal Properties: A Common Thread
Limits and left adjoints share a fundamental connection through universal properties, serving as core tools in category theory for characterizing objects uniquely up to isomorphism. Limits are defined by universal cones projecting into a diagram, ensuring the existence of a most general mapping satisfying specific commutativity conditions, while left adjoints arise from universal morphisms that provide optimal approximations to functors. Both universal properties encapsulate optimality and uniqueness criteria, highlighting the deep interplay between constructions like limits and adjoint functors across diverse categorical contexts.
Constructing Limits via Adjoints
Limits in category theory can be constructed using left adjoint functors by exploiting the universal property of adjunctions. Specifically, given a functor with a left adjoint, the limit of a diagram can be realized as the image of an adjoint applied to certain terminal objects or cones, which simplifies the limit construction by translating it into a representability problem. This approach leverages the fact that right adjoints preserve limits, enabling the explicit computation of limits through left adjoint-induced structures.
Key Differences Between Limits and Left Adjoints
Limits in category theory represent universal cones defining objects that factorize diagrams uniquely, emphasizing universality and preservation of structures. Left adjoints are functors characterized by their ability to preserve colimits and establish a natural bijection between hom-sets, reflecting an intrinsic relationship with right adjoints. Key differences include limits being specific universal constructions within categories, whereas left adjoints function as functors with adjoint relationships, focusing on preservation properties and existence of natural transformations.
Examples in Algebra and Topology
Limits in category theory, such as inverse limits, provide universal constructions capturing algebraic structures like projective limits of groups or rings, exemplified by the limit of a sequence of quotient groups. Left adjoints, often appearing as free constructions, produce objects like free groups or free modules that universally map into algebraic structures from sets. In topology, limits correspond to inverse limits of topological spaces ensuring continuity conditions, while left adjoints manifest as functors assigning free topological groups to spaces, exemplifying the interplay between algebraic and topological contexts.
Applications of Limits and Adjoints in Mathematics
Limits and left adjoints play crucial roles in category theory and its applications across mathematics, particularly in algebra, topology, and logic. Limits provide a way to construct universal objects from diagrams, enabling the analysis of structures by capturing their global behavior, while left adjoints facilitate the transfer of structures and properties between categories through universal morphisms. These concepts underpin the formulation of adjunctions, enabling the systematic study of equivalences, dualities, and representable functors essential for modern mathematical frameworks such as homological algebra and sheaf theory.
Conclusion: Bridging Limits and Left Adjoints
Limits in category theory characterize universal constructions that capture the notion of "best approximations" to diagrams, while left adjoints preserve colimits and reflect a deeper structural relationship between categories. The connection lies in that every right adjoint functor, by definition, preserves all limits, demonstrating how limits serve as a foundational concept for adjunctions. Understanding this bridge underscores the role of limits in identifying and constructing left adjoints, offering a unified perspective on categorical completeness and adjoint functor pairs.
Limit Infographic
 libterm.com
libterm.com